Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T02:03:47.273Z Has data issue: false hasContentIssue false
  • English
  • Français

The ideal structures of self-similar 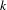$k$-graph C*-algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  11 June 2020

HUI LI  and
DILIAN YANG
HUI LI
Affiliation:
Department of Mathematics and Physics, North China Electric Power University, Beijing 102206, China (e-mail: lihui8605@hotmail.com)
DILIAN YANG
Affiliation:
Department of Mathematics & Statistics, University of Windsor, Windsor, Ontario N9B 3P4, Canada (e-mail: dyang@uwindsor.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 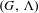$(G,\unicode[STIX]{x1D6EC})$ be a self-similar 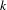$k$-graph with a possibly infinite vertex set 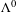$\unicode[STIX]{x1D6EC}^{0}$. We associate a universal C*-algebra 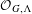${\mathcal{O}}_{G,\unicode[STIX]{x1D6EC}}$ to 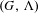$(G,\unicode[STIX]{x1D6EC})$. The main purpose of this paper is to investigate the ideal structures of 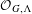${\mathcal{O}}_{G,\unicode[STIX]{x1D6EC}}$. We prove that there exists a one-to-one correspondence between the set of all 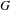$G$-hereditary and 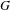$G$-saturated subsets of 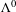$\unicode[STIX]{x1D6EC}^{0}$ and the set of all gauge-invariant and diagonal-invariant ideals of 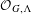${\mathcal{O}}_{G,\unicode[STIX]{x1D6EC}}$. Under some conditions, we characterize all primitive ideals of 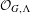${\mathcal{O}}_{G,\unicode[STIX]{x1D6EC}}$. Moreover, we describe the Jacobson topology of some concrete examples, which includes the C*-algebra of the product of odometers. On the way to our main results, we study self-similar $P$-graph C*-algebras in depth.

Keywords

self-similar k-graphC*-algebragauge-invariant idealprimitive idealUniversal Coefficient Theorem

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L55: Noncommutative dynamical systems

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 8 , August 2021 , pp. 2480 - 2507
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Albandik, S. and Meyer, R.. Product systems over Ore monoids. Doc. Math. 20 (2015), 1331–1402.Google Scholar
Brown, J., Clark, L. O., Farthing, C. and Sims, A.. Simplicity of algebras associated to étale groupoids. Semigroup Forum 88 (2014), 433–452.Google Scholar
Brown, N. P. and Ozawa, N.. C∗-Algebras and Finite-dimensional Approximations. American Mathematical Society, Providence, RI, 2008.Google Scholar
Carlsen, T. M., Kang, S., Shotwell, J. and Sims, A.. The primitive ideals of the Cuntz–Krieger algebra of a row-finite higher-rank graph with no sources. J. Funct. Anal. 266 (2014), 2570–2589.Google Scholar
Carlsen, T. M., Larsen, N. S., Sims, A. and Vittadello, S. T.. Co-universal algebras associated to product systems, and gauge-invariant uniqueness theorems. Proc. Lond. Math. Soc. (3) 103 (2011), 563–600.Google Scholar
Dixmier, J.. C ∗-Algebras (North-Holland Mathematical Library, Vol. 15). North-Holland, Amsterdam, 1977, translated from the French by Jellett, Francis.Google Scholar
Dixmier, J.. Von Neumann Algebras. North-Holland, Amsterdam–New York, 1981, with a Preface by Lance, E. C., translated from the second French edition by Jellett, F..Google Scholar
Exel, R.. Non-Hausdorff étale groupoids. Proc. Amer. Math. Soc. 139 (2011), 897–907.Google Scholar
Exel, R. and Pardo, E.. Self-similar graphs, a unified treatment of Katsura and Nekrashevych C∗-algebras. Adv. Math. 306 (2017), 1046–1129.Google Scholar
Exel, R., Pardo, E. and Starling, C.. $C^{\ast }$ -algebras of self-similar graphs over arbitrary graphs. Preprint, 2018, arXiv:1807.01686.Google Scholar
Folland, G. B.. A Course in Abstract Harmonic Analysis. CRC Press, Boca Raton, FL, 1995.Google Scholar
Fowler, N. J.. Discrete product systems of Hilbert bimodules. Pacific J. Math. 204 (2002), 335–375.Google Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A.. KMS states on the C∗-algebra of a higher-rank graph and periodicity in the path space. J. Funct. Anal. 268 (2015), 1840–1875.Google Scholar
Hungerford, T. W.. Algebra. Springer, New York, 1980, reprint of the 1974 original.Google Scholar
Kang, S. and Pask, D.. Aperiodicity and primitive ideals of row-finite k-graphs. Internat. J. Math. 25 (2014), article ID 145022, 25 pages.Google Scholar
Katsura, T.. The ideal structures of crossed products of Cuntz algebras by quasi-free actions of abelian groups. Canad. J. Math. 55 (2003), 1302–1338.Google Scholar
Katsura, T.. A construction of actions on Kirchberg algebras which induce given actions on their K-groups. J. Reine Angew. Math. 617 (2008), 27–65.Google Scholar
Kumjian, A. and Pask, D.. Higher rank graph C ∗-algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Li, H. and Yang, D.. Boundary quotient C ∗-algebras of products of odometers. Canad. J. Math. 71 (2019), 183–212.Google Scholar
Li, H. and Yang, D.. KMS states of self-similar k-graph C ∗-algebras. J. Funct. Anal. 276 (2019), 3795–3831.Google Scholar
Li, H. and Yang, D.. Self-similar  $k$ -graph  $C^{\ast }$ -algebras. Int. Math. Res. Not. IMRN, doi:10.1093/imrn/rnz146.Google Scholar
Murphy, G. J.. C∗-Algebras and Operator Theory. Academic Press, Boston, MA, 1990.Google Scholar
Nekrashevych, V.. C ∗-algebras and self-similar groups. J. Reine Angew. Math. 630 (2009), 59–123.Google Scholar
Pask, D., Rennie, A. and Sims, A.. The noncommutative geometry of k-graph C∗ -algebras. J. K-Theory 1 (2008), 259–304.Google Scholar
Raeburn, I., Sims, A. and Yeend, T.. Higher-rank graphs and their C ∗-algebras. Proc. Edinb. Math. Soc. (2) 46 (2003), 99–115.Google Scholar
Raeburn, I. and Williams, D. P.. Morita Equivalence and Continuous-trace C ∗-Algebras. American Mathematical Society, Providence, RI, 1998.Google Scholar
Rainone, T. and Sims, A.. A dichotomy for groupoid C ∗-algebras. Ergod. Th. & Dynam. Sys. 40(2) (2020), 521–563.Google Scholar
Renault, J.. A Groupoid Approach to C ∗-Algebras. Springer, Berlin, 1980.Google Scholar
Williams, D. P.. Crossed Products of C ∗-Algebras. American Mathematical Society, Providence, RI, 2007.Google Scholar
Yang, D.. Periodic k-graph algebras revisited. J. Aust. Math. Soc. 99 (2015), 267–286.Google Scholar