Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T23:10:34.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrality properties of Böttcher coordinates for one-dimensional superattracting germs

Published online by Cambridge University Press:  06 July 2018

ADRIANA SALERNO  and
JOSEPH H. SILVERMAN
ADRIANA SALERNO
Affiliation:
Department of Mathematics, Bates College, Lewiston, ME 04240, USA email asalerno@bates.edu
JOSEPH H. SILVERMAN
Affiliation:
Mathematics Department, Box 1917, Brown University, Providence, RI 02912, USA email jhs@math.brown.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 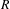$R$ be a ring of characteristic $0$ with field of fractions 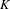$K$ and let 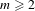$m\geq 2$. The Böttcher coordinate of a power series 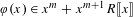$\unicode[STIX]{x1D711}(x)\in x^{m}+x^{m+1}R\unicode[STIX]{x27E6}x\unicode[STIX]{x27E7}$ is the unique power series 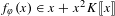$f_{\unicode[STIX]{x1D711}}(x)\in x+x^{2}K\unicode[STIX]{x27E6}x\unicode[STIX]{x27E7}$ satisfying 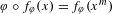$\unicode[STIX]{x1D711}\circ f_{\unicode[STIX]{x1D711}}(x)=f_{\unicode[STIX]{x1D711}}(x^{m})$. In this paper we study the integrality properties of the coefficients of 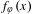$f_{\unicode[STIX]{x1D711}}(x)$, partly for their intrinsic interest and partly for potential applications to 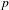$p$-adic dynamics. Results include: (1) if 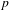$p$ is prime and 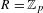$R=\mathbb{Z}_{p}$ and 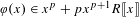$\unicode[STIX]{x1D711}(x)\in x^{p}+px^{p+1}R\unicode[STIX]{x27E6}x\unicode[STIX]{x27E7}$, then 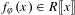$f_{\unicode[STIX]{x1D711}}(x)\in R\unicode[STIX]{x27E6}x\unicode[STIX]{x27E7}$. (2) If 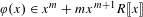$\unicode[STIX]{x1D711}(x)\in x^{m}+mx^{m+1}R\unicode[STIX]{x27E6}x\unicode[STIX]{x27E7}$, then 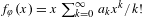$f_{\unicode[STIX]{x1D711}}(x)=x\sum _{k=0}^{\infty }a_{k}x^{k}/k!$ with all 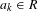$a_{k}\in R$. (3) In (2), if 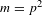$m=p^{2}$, then 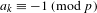$a_{k}\equiv -1~\text{(mod}~p\text{)}$ for all 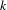$k$ that are powers of 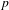$p$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 248 - 271
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, J. P., Ghioca, D. and Tucker, T. J.. The dynamical Mordell–Lang problem for étale maps. Amer. J. Math. 132(6) (2010), 1655–1675.Google Scholar
Böttcher, L. E. B.. The principal laws of convergence of iterates and their application to analysis. Izv. Kazan. Fiz.-Mat. Obshch. 14 (1904), 155–234 (in Russian).Google Scholar
Buff, X., Epstein, A. L. and Koch, S.. Böttcher coordinates. Indiana Univ. Math. J. 61(5) (2012), 1765–1799.Google Scholar
DeMarco, L., Ghioca, D., Krieger, H., Nguyen, K., Tucker, T. and Ye, H.. Bounded height in families of dynamical systems. Int. Math. Res. Not. Published online 29 August 2017,https://doi.org/10.1093/imrn/rnx174.Google Scholar
Favre, C.. Classification of 2-dimensional contracting rigid germs and Kato surfaces. I. J. Math. Pures Appl. (9) 79(5) (2000), 475–514.Google Scholar
Favre, C. and Jonsson, M.. Eigenvaluations. Ann. Sci. Éc. Norm. Supér. (4) 40(2) (2007), 309–349.Google Scholar
Ghioca, D. and Tucker, T. J.. Periodic points, linearizing maps, and the dynamical Mordell–Lang problem. J. Number Theory 129(6) (2009), 1392–1403.10.1016/j.jnt.2008.09.014Google Scholar
Gignac, W. and Ruggiero, M.. Growth of attraction rates for iterates of a superattracting germ in dimension two. Indiana Univ. Math. J. 63(4) (2014), 1195–1234.Google Scholar
Herman, M. and Yoccoz, J.-C.. Generalizations of some theorems of small divisors to non-Archimedean fields. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007) . Springer, Berlin, 1983, pp. 408–447.Google Scholar
Hubbard, J. H. and Papadopol, P.. Superattractive fixed points in C n . Indiana Univ. Math. J. 43(1) (1994), 321–365.Google Scholar
Ingram, P.. Arboreal Galois representations and uniformization of polynomial dynamics. Bull. Lond. Math. Soc. 45(2) (2013), 301–308.Google Scholar
Johnson, W. P.. The curious history of Faà di Bruno’s formula. Amer. Math. Monthly 109(3) (2002), 217–234.Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160) , 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Roman, S.. The formula of Faà di Bruno. Amer. Math. Monthly 87(10) (1980), 805–809.Google Scholar
Ruggiero, M.. Contracting rigid germs in higher dimensions. Ann. Inst. Fourier (Grenoble) 63(5) (2013), 1913–1950.Google Scholar
Ruggiero, M.. Classification of one-dimensional superattracting germs in positive characteristic. Ergod. Th. & Dynam. Sys. 35(7) (2015), 2242–2268.Google Scholar
Silverman, J. H.. The Arithmetic of Elliptic Curves (Graduate Texts in Mathematics, 106) , 2nd edn. Springer, Dordrecht, 2009.Google Scholar
Spencer, M. P.. Moduli spaces of power series in finite characteristic. PhD Thesis, Brown University, 2011.Google Scholar
Ueda, T.. Complex dynamical systems on projective spaces. Topics around chaotic dynamical systems (Kyoto, 1992). Sūrikaisekikenkyūsho Kōkyūroku 814 (1992), 169–186 (in Japanese).Google Scholar
Ueno, K.. Böttcher coordinates at superattracting fixed points of holomorphic skew products. Conform. Geom. Dyn. 20 (2016), 43–57.Google Scholar
Ushiki, S.. Böttcher’s theorem and super-stable manifolds for multidimensional complex dynamical systems. Proc. RIMS Conf. Structure and Bifurcations of Dynamical Systems, Kyoto, Japan, 18–21 February 1992 (Advanced Series in Dynamical Systems, 11) . Ed. Ushiki, S.. World Scientific, Singapore, 1992, pp. 168–184.Google Scholar