Article contents
Invariant circles and depinning transition
Published online by Cambridge University Press: 22 September 2016
Abstract
We associate the existence or non-existence of rotational invariant circles of an area-preserving twist map on the cylinder with a physically motivated quantity, the depinning force, which is a critical value in the depinning transition. Assume that 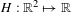 $H:\mathbb{R}^{2}\mapsto \mathbb{R}$ is a
$H:\mathbb{R}^{2}\mapsto \mathbb{R}$ is a 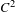 $C^{2}$ generating function of an exact area-preserving twist map
$C^{2}$ generating function of an exact area-preserving twist map 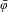 $\bar{\unicode[STIX]{x1D711}}$ and consider the tilted Frenkel–Kontorova (FK) model:
$\bar{\unicode[STIX]{x1D711}}$ and consider the tilted Frenkel–Kontorova (FK) model: 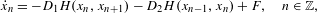 $$\begin{eqnarray}{\dot{x}}_{n}=-D_{1}H(x_{n},x_{n+1})-D_{2}H(x_{n-1},x_{n})+F,\quad n\in \mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}{\dot{x}}_{n}=-D_{1}H(x_{n},x_{n+1})-D_{2}H(x_{n-1},x_{n})+F,\quad n\in \mathbb{Z},\end{eqnarray}$$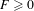 $F\geq 0$ is the driving force. The depinning force is the critical value
$F\geq 0$ is the driving force. The depinning force is the critical value 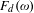 $F_{d}(\unicode[STIX]{x1D714})$ depending on the mean spacing
$F_{d}(\unicode[STIX]{x1D714})$ depending on the mean spacing  $\unicode[STIX]{x1D714}$ of particles, above which the tilted FK model is sliding, and below which the particles are pinned. We prove that there exists an invariant circle with irrational rotation number
$\unicode[STIX]{x1D714}$ of particles, above which the tilted FK model is sliding, and below which the particles are pinned. We prove that there exists an invariant circle with irrational rotation number  $\unicode[STIX]{x1D714}$ for
$\unicode[STIX]{x1D714}$ for 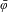 $\bar{\unicode[STIX]{x1D711}}$ if and only if
$\bar{\unicode[STIX]{x1D711}}$ if and only if 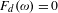 $F_{d}(\unicode[STIX]{x1D714})=0$ . For rational
$F_{d}(\unicode[STIX]{x1D714})=0$ . For rational  $\unicode[STIX]{x1D714}$ ,
$\unicode[STIX]{x1D714}$ , 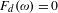 $F_{d}(\unicode[STIX]{x1D714})=0$ is equivalent to the existence of an invariant circle on which
$F_{d}(\unicode[STIX]{x1D714})=0$ is equivalent to the existence of an invariant circle on which  $\bar{\unicode[STIX]{x1D711}}$ is topologically conjugate to the rational rotation with rotation number
$\bar{\unicode[STIX]{x1D711}}$ is topologically conjugate to the rational rotation with rotation number  $\unicode[STIX]{x1D714}$ . Such conclusions were claimed much earlier by Aubry et al. We also show that the depinning force
$\unicode[STIX]{x1D714}$ . Such conclusions were claimed much earlier by Aubry et al. We also show that the depinning force 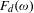 $F_{d}(\unicode[STIX]{x1D714})$ is continuous at irrational
$F_{d}(\unicode[STIX]{x1D714})$ is continuous at irrational  $\unicode[STIX]{x1D714}$ .
$\unicode[STIX]{x1D714}$ .
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 10
- Cited by

