Article contents
Invariant tori and topological entropy in Tonelli Lagrangian systems on the 2-torus
Published online by Cambridge University Press: 19 March 2015
Abstract
We study the Euler–Lagrange flow of a Tonelli Lagrangian on the 2-torus 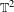 $\mathbb{T}^{2}$ at a fixed energy level
$\mathbb{T}^{2}$ at a fixed energy level 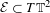 ${\mathcal{E}}\subset T\mathbb{T}^{2}$ strictly above Mañé’s strict critical value. We prove that, if for some rational direction
${\mathcal{E}}\subset T\mathbb{T}^{2}$ strictly above Mañé’s strict critical value. We prove that, if for some rational direction 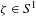 ${\it\zeta}\in S^{1}$ there is no invariant graph
${\it\zeta}\in S^{1}$ there is no invariant graph 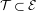 ${\mathcal{T}}\subset {\mathcal{E}}$ over
${\mathcal{T}}\subset {\mathcal{E}}$ over 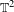 $\mathbb{T}^{2}$ for the Euler–Lagrange flow with the property that all orbits on
$\mathbb{T}^{2}$ for the Euler–Lagrange flow with the property that all orbits on 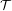 ${\mathcal{T}}$ have an asymptotic direction equal to
${\mathcal{T}}$ have an asymptotic direction equal to 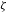 ${\it\zeta}$ , then there are chaotic dynamics in
${\it\zeta}$ , then there are chaotic dynamics in 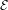 ${\mathcal{E}}$ . This implies that, if the topological entropy of the Euler–Lagrange flow in
${\mathcal{E}}$ . This implies that, if the topological entropy of the Euler–Lagrange flow in 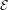 ${\mathcal{E}}$ vanishes, then in
${\mathcal{E}}$ vanishes, then in 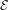 ${\mathcal{E}}$ there are invariant graphs for all asymptotic directions
${\mathcal{E}}$ there are invariant graphs for all asymptotic directions 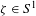 ${\it\zeta}\in S^{1}$ and integrable-like behavior on a large scale.
${\it\zeta}\in S^{1}$ and integrable-like behavior on a large scale.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 2
- Cited by

