Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-25T19:59:39.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Lyapunov-maximizing measures for pairs of weighted shift operators

Published online by Cambridge University Press:  04 May 2017

IAN D. MORRIS
IAN D. MORRIS*
Affiliation:
Department of Mathematics, University of Surrey, Guildford GU2 7XH, UK email i.morris@surrey.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by recent investigations of ergodic optimization for matrix cocycles, we study the measures of the maximum top Lyapunov exponent for pairs of bounded weighted shift operators on a separable Hilbert space. We prove that, for generic pairs of weighted shift operators, the Lyapunov-maximizing measure is unique, and show that there exist pairs of operators whose unique Lyapunov-maximizing measure takes any prescribed value less than 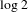$\log 2$ for its metric entropy. We also show that, in contrast to the matrix case, the Lyapunov-maximizing measures of pairs of bounded operators are, in general, not characterized by their supports: we construct explicitly a pair of operators and a pair of ergodic measures on the 2-shift with identical supports, such that one of the two measures is Lyapunov-maximizing for the pair of operators and the other measure is not. Our proofs make use of the Ornstein 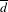$\overline{d}$-metric to estimate differences in the top Lyapunov exponent of a pair of weighted shift operators as the underlying measure is varied.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 225 - 247
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berger, M. A. and Wang, Y.. Bounded semigroups of matrices. Linear Algebra Appl. 166 (1992), 21–27.Google Scholar
Blondel, V. D., Theys, J. and Vladimirov, A. A.. An elementary counterexample to the finiteness conjecture. SIAM J. Matrix Anal. Appl. 24(4) (2003), 963–970 (electronic).Google Scholar
Bochi, J.. Inequalities for numerical invariants of sets of matrices. Linear Algebra Appl. 368 (2003), 71–81.Google Scholar
Bochi, J. and Rams, M.. The entropy of Lyapunov-optimizing measures of some matrix cocycles. J. Mod. Dyn. 10 (2016), 255–286.Google Scholar
Bousch, T.. La condition de Walters. Ann. Sci. Éc. Norm. Supér. (4) 34(2) (2001), 287–311.Google Scholar
Bousch, T.. Nouvelle preuve d’un théorème de Yuan et Hunt. Bull. Soc. Math. France 136(2) (2008), 227–242.Google Scholar
Bousch, T. and Jenkinson, O.. Cohomology classes of dynamically non-negative C k functions. Invent. Math. 148(1) (2002), 207–217.Google Scholar
Bousch, T. and Mairesse, J.. Asymptotic height optimization for topical IFS, Tetris heaps, and the finiteness conjecture. J. Amer. Math. Soc. 15(1) (2002), 77–111 (electronic).Google Scholar
Contreras, G.. Ground states are generically a periodic orbit. Invent. Math. 205 (2016), 383–412.Google Scholar
Contreras, G., Lopes, A. O. and Thieullen, P.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21(5) (2001), 1379–1409.Google Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527) . Springer, Berlin–New York, 1976.Google Scholar
Elsner, L.. The generalized spectral-radius theorem: an analytic-geometric proof. Proc. Workshop Nonnegative Matrices, Applications and Generalizations and Eighth Haifa Matrix Theory Conf. (Haifa, 1993) . Linear Algebra Appl. 220 (1995), 151–159.Google Scholar
Glasner, E.. Ergodic Theory Via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Grillenberger, C.. Constructions of strictly ergodic systems. I. Given entropy. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 25 (1972/73), 323–334.Google Scholar
Gurvits, L.. Stability of discrete linear inclusion. Linear Algebra Appl. 231 (1995), 47–85.Google Scholar
Hare, K. G., Morris, I. D. and Sidorov, N.. Extremal sequences of polynomial complexity. Math. Proc. Cambridge Philos. Soc. 155(2) (2013), 191–205.Google Scholar
Hare, K. G., Morris, I. D., Sidorov, N. and Theys, J.. An explicit counterexample to the Lagarias–Wang finiteness conjecture. Adv. Math. 226 (2011), 4667–4701.Google Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15(1) (2006), 197–224.Google Scholar
Jenkinson, O.. Every ergodic measure is uniquely maximizing. Discrete Contin. Dyn. Syst. 16(2) (2006), 383–392.Google Scholar
Jenkinson, O. and Pollicott, M.. Joint spectral radius, Sturmian measures, and the finiteness conjecture. Preprint, 2015, arXiv:1501.03419. Erg. Th. & Dynam. Sys. accepted.Google Scholar
Jungers, R.. The Joint Spectral Radius: Theory and Applications (Lecture Notes in Control and Information Sciences, 385) . Springer, Berlin, 2009.Google Scholar
Kozyakin, V. S.. Structure of extremal trajectories of discrete linear systems and the finiteness conjecture. Autom. Remote Control 68 (2007), 174–209.Google Scholar
Lagarias, J. C. and Wang, Y.. The finiteness conjecture for the generalized spectral radius of a set of matrices. Linear Algebra Appl. 214 (1995), 17–42.Google Scholar
Morris, I. D.. A sufficient condition for the subordination principle in ergodic optimization. Bull. Lond. Math. Soc. 39(2) (2007), 214–220.Google Scholar
Morris, I. D.. Maximizing measures of generic Hölder functions have zero entropy. Nonlinearity 21(5) (2008), 993–1000.Google Scholar
Morris, I. D.. Criteria for the stability of the finiteness property and for the uniqueness of Barabanov norms. Linear Algebra Appl. 433(7) (2010), 1301–1311.Google Scholar
Morris, I. D.. Ergodic optimization for generic continuous functions. Discrete Contin. Dyn. Syst. 27(1) (2010), 383–388.Google Scholar
Morris, I. D.. Mather sets for sequences of matrices and applications to the study of joint spectral radii. Proc. Lond. Math. Soc. (3) 107(1) (2013), 121–150.Google Scholar
Oxtoby, J. C.. Ergodic sets. Bull. Amer. Math. Soc. 58 (1952), 116–136.Google Scholar
Schreiber, S. J.. On growth rates of subadditive functions for semiflows. J. Differential Equations 148(2) (1998), 334–350.Google Scholar
Shields, P. C.. The Ergodic Theory of Discrete Sample Paths (Graduate Studies in Mathematics, 13) . American Mathematical Society, Providence, RI, 1996.Google Scholar
Sturman, R. and Stark, J.. Semi-uniform ergodic theorems and applications to forced systems. Nonlinearity 13(1) (2000), 113–143.Google Scholar
Williams, S.. Toeplitz minimal flows which are not uniquely ergodic. Z. Wahrsch. Verw. Gebiete 67(1) (1984), 95–107.Google Scholar
Yuan, G. and Hunt, B. R.. Optimal orbits of hyperbolic systems. Nonlinearity 12(4) (1999), 1207–1224.Google Scholar