Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T15:19:08.129Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of ergodic measures for transitive subshifts under the regular bispecial condition

Part of: Measure-theoretic ergodic theory Topological dynamics Ergodic theory

Published online by Cambridge University Press:  29 December 2020

MICHAEL DAMRON  and
JON FICKENSCHER
MICHAEL DAMRON
Affiliation:
School of Mathematics, Georgia Institute of Technology, 686 Cherry Street, Atlanta, GA30332, USA (e-mail:mdamron6@math.gatech.edu)
JON FICKENSCHER*
Affiliation:
Mathematics Department, Princeton University, Fine Hall, Washington Road, Princeton, NJ08544, USA
*
e-mail:jonfick@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

If 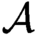$\mathcal {A}$ is a finite set (alphabet), the shift dynamical system consists of the space 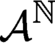$\mathcal {A}^{\mathbb {N}}$ of sequences with entries in 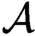$\mathcal {A}$ , along with the left shift operator S. Closed S-invariant subsets are called subshifts and arise naturally as encodings of other systems. In this paper, we study the number of ergodic measures for transitive subshifts under a condition (‘regular bispecial condition’) on the possible extensions of words in the associated language. Our main result shows that under this condition, the subshift can support at most 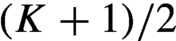$({K+1})/{2}$ ergodic measures, where K is the limiting value of $p(n+1)-p(n)$ , and p is the complexity function of the language. As a consequence, we answer a question of Boshernitzan from 1984, providing a combinatorial proof for the bound on the number of ergodic measures for interval exchange transformations.

Keywords

symbolic dynamicsclassical ergodic theoryformal languages

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 28D05: Measure-preserving transformations 37A05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 1 , January 2022 , pp. 86 - 140
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper is dedicated to Michael Boshernitzan, whose enthusiasm and passion remain an inspiration for mathematicians, both present and future.

References

REFERENCES

Avila, A. and Resende, M. J.. Exponential mixing for the Teichmüller flow in the space of quadratic differentials. Comment. Math. Helv. 87(3) (2012), 589–638.CrossRefGoogle Scholar
Boissy, C. and Lanneau, E.. Dynamics and geometry of the Rauzy-Veech induction for quadratic differentials. Ergod. Th. & Dynam. Sys. 29(3) (2009), 767–816.CrossRefGoogle Scholar
Boshernitzan, M.. A unique ergodicity of minimal symbolic flows with linear block growth. J. Anal. Math. 44(1) (1984), 77–96.CrossRefGoogle Scholar
Cassaigne, J.. Special factors of sequences with linear subword complexity. Developments in Language Theory, II (Magdeburg, 1995). World Scientific Publishing, River Edge, NJ, 1996, pp. 25–34.Google Scholar
Cyr, V. and Kra, B.. Counting generic measures for a subshift of linear growth. J. Eur. Math. Soc. (JEMS) 21(2) (2019), 355–380.CrossRefGoogle Scholar
Damron, M. and Fickenscher, J.. On the number of ergodic measures for minimal shifts with eventually constant complexity growth. Ergod. Th. & Dynam. Sys. 37(7) (2017), 2099–2130.CrossRefGoogle Scholar
Dolce, F. and Perrin, D.. Eventually dendric shifts. Computer Science – Theory and Applications. Ed. van Bevern, R. and Kucherov, G.. Springer International Publishing, Cham, 2019, pp. 106–118.CrossRefGoogle Scholar
Dolce, F. and Perrin, D.. Return words and bifix codes in eventually dendric sets. Combinatorics on Words. Ed. Mercaş, R. and Reidenbach, D.. Springer International Publishing, Cham, 2019, pp. 167–179.CrossRefGoogle Scholar
Fickenscher, J.. Self-inverses, Lagrangian permutations and minimal interval exchange transformations with many ergodic measures. Commun. Contemp. Math. 16(1) (2014), 1350019, 51.CrossRefGoogle Scholar
Ferenczi, S. and Monteil, T.. Infinite words with uniform frequencies, and invariant measures. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135). Cambridge University Press, Cambridge, 2010, pp. 373–409.Google Scholar
Fogg, N. P.. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794). Ed. Berthé, V., Ferenczi, S., Mauduit, C. and Siegel, A.. Springer, Berlin, 2002.CrossRefGoogle Scholar
Ferenczi, S. and Zamboni, L. Q.. Languages of $k$ -interval exchange transformations. Bull. Lond. Math. Soc. 40(4) (2008), 705–714.CrossRefGoogle Scholar
Katok, A.. Invariant measures of flows on oriented surfaces. Soviet Math. Dokl. 14(4) (1973), 1104–1108.Google Scholar
Kryloff, N. and Bogoliouboff, N.. La théorie générale de la mesure dans son application à l’étude des systèmes dynamiques de la mécanique non linéaire. Ann. of Math. (2) 38(1) (1937), 65–113.CrossRefGoogle Scholar
Keane, M.. Interval exchange transformations. Math. Z. 141 (1975), 25–31.CrossRefGoogle Scholar
Keane, M.. Non-ergodic interval exchange transformations. Israel J. Math. 26(2) (1977), 188–196.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics. Amer. J. Math. 60(4) (1938), 815–866.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62(1) (1940), 1–42.CrossRefGoogle Scholar
Veech, W. A.. Interval exchange transformations. J. Anal. Math. 33 (1978), 222–272.CrossRefGoogle Scholar
Veech, W. A.. Gauss measures for transformations on the space of interval exchange maps. Ann. of Math. (2) 115(1) (1982), 201–242.CrossRefGoogle Scholar
Yoccoz, J.-C.. Interval exchange maps and translation surfaces. Homogeneous Flows, Moduli Spaces and Arithmetic (Clay Mathematics Proceedings, 10). American Mathematical Society, Providence, RI, 2010, pp. 1–69.Google Scholar