Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-10T20:07:03.803Z Has data issue: false hasContentIssue false
  • English
  • Français

On simplicity of intermediate 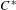$C^{\ast }$-algebras

Part of: Ergodic theory Selfadjoint operator algebras

Published online by Cambridge University Press:  06 June 2019

TATTWAMASI AMRUTAM  and
MEHRDAD KALANTAR
TATTWAMASI AMRUTAM
Affiliation:
Department of Mathematics, 3551 Cullen Blvd, Room 641, Philip Guthrie Hoffman Hall, Houston, TX77204, USA email tamrutam@math.uh.edu, kalantar@math.uh.edu
MEHRDAD KALANTAR
Affiliation:
Department of Mathematics, 3551 Cullen Blvd, Room 641, Philip Guthrie Hoffman Hall, Houston, TX77204, USA email tamrutam@math.uh.edu, kalantar@math.uh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove simplicity of all intermediate 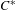$C^{\ast }$-algebras 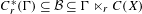$C_{r}^{\ast }(\unicode[STIX]{x1D6E4})\subseteq {\mathcal{B}}\subseteq \unicode[STIX]{x1D6E4}\ltimes _{r}C(X)$ in the case of minimal actions of 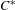$C^{\ast }$-simple groups $\unicode[STIX]{x1D6E4}$ on compact spaces 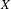$X$. For this, we use the notion of stationary states, recently introduced by Hartman and Kalantar [Stationary 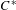$C^{\ast }$-dynamical systems. Preprint, 2017, arXiv:1712.10133]. We show that the Powers’ averaging property holds for the reduced crossed product 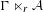$\unicode[STIX]{x1D6E4}\ltimes _{r}{\mathcal{A}}$ for any action 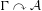$\unicode[STIX]{x1D6E4}\curvearrowright {\mathcal{A}}$ of a 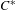$C^{\ast }$-simple group $\unicode[STIX]{x1D6E4}$ on a unital 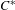$C^{\ast }$-algebra 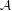${\mathcal{A}}$, and use it to prove a one-to-one correspondence between stationary states on 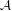${\mathcal{A}}$ and those on 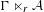$\unicode[STIX]{x1D6E4}\ltimes _{r}{\mathcal{A}}$.

Keywords

group actionsoperator algebrascrossed product C∗ -algebrasstationary group actionsC∗ -simplicity

MSC classification

Primary: 46L10: General theory of von Neumann algebras 46L55: Noncommutative dynamical systems
Secondary: 37A55: Relations with the theory of $C^*$-algebras 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 12 , December 2020 , pp. 3181 - 3187
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archbold, R. J. and Spielberg, J. S.. Topologically free actions and ideals in discrete C ∗ -dynamical systems. Proc. Edinb. Math. Soc. (2) 37 (1994), 119–124.Google Scholar
Bédos, E.. Discrete groups and simple C ∗ -algebras. Math. Proc. Cambridge Philos. Soc. 109(3) (1991), 521–537.Google Scholar
Breuillard, E., Kalantar, M., Kennedy, M. and Ozawa, N.. C ∗ -simplicity and the unique trace property for discrete groups. Publ. Math. Inst. Hautes Études Sci. 126 (2017), 35–71.Google Scholar
Brown, N. and Ozawa, N.. C ∗ -Algebras and Finite-dimensional Approximations (Graduate Studies in Mathematics, 88). American Mathematical Society, Providence, RI, 2008.Google Scholar
Bryder, R. S. and Kennedy, M.. Reduced twisted crossed products over C ∗ -simple groups. Int. Math. Res. Not. IMRN 6 (2018), 1638–1655.Google Scholar
de la Harpe, P. and Skandalis, G.. Powers’ property and simple C ∗ -algebras. Math. Ann. 273 (1986), 241–250.Google Scholar
Elliott, G. A.. Some simple C ∗ -algebras constructed as crossed products with discrete outer automorphism groups. Publ. Res. Inst. Math. Sci. 16(1) (1980), 299–311.Google Scholar
Haagerup, U.. A new look at C ∗ -simplicity and the unique trace property of a group. Operator Algebras and Applications (The Abel Symposium 2015) (Abel Sympia, 12). Springer, Cham, 2017, pp. 167–176.Google Scholar
Hartman, Y. and Kalantar, M.. Stationary $C^{\ast }$-dynamical systems. Preprint, 2017, arXiv:1712.10133.Google Scholar
Jang, S. Y. and Lee, S. G.. Simplicity of crossed products of C ∗ -algebras. Proc. Amer. Math. Soc. 118(3) (1993), 823–826.Google Scholar
Kalantar, M. and Kennedy, M.. Boundaries of reduced C ∗ -algebras of discrete groups. J. Reine Angew. Math. 727 (2017), 247–267.Google Scholar
Kawamura, S. and Tomiyama, J.. Properties of topological dynamical systems and corresponding C ∗ -algebras. Tokyo J. Math. 13 (1990), 251–257.Google Scholar
Kennedy, M.. An intrinsic characterization of $C^{\ast }$-simplicity. Ann. Sci. Éc. Norm. Supér., accepted. Preprint, 2015, arXiv:1509.01870.Google Scholar
Sierakowski, A.. The ideal structure of reduced crossed products. Münster J. Math. 3 (2010), 237–261.Google Scholar
Suzuki, Y.. Minimal ambient nuclear C∗ -algebras. Adv. Math. 304 (2017), 421–433.Google Scholar
Suzuki, Y.. Complete descriptions of intermediate operator algebras by intermediate extensions of dynamical systems. Commun. Math. Phys., accepted. Preprint, 2018, arXiv:1805.02077.Google Scholar
Takesaki, M.. On the cross-norm of the direct product of C ∗ -algebras. Tôhoku Math. J. (2) 16 (1964), 111–122.Google Scholar