Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T06:27:00.342Z Has data issue: false hasContentIssue false
  • English
  • Français

On the computability of rotation sets and their entropies

Published online by Cambridge University Press:  10 August 2018

MICHAEL A. BURR ,
MARTIN SCHMOLL  and
CHRISTIAN WOLF
MICHAEL A. BURR
Affiliation:
Department of Mathematical Sciences, Clemson University, Clemson, SC 29634, USA email burr2@clemson.edu, schmoll@clemson.edu
MARTIN SCHMOLL
Affiliation:
Department of Mathematical Sciences, Clemson University, Clemson, SC 29634, USA email burr2@clemson.edu, schmoll@clemson.edu
CHRISTIAN WOLF
Affiliation:
Department of Mathematics, The City College of New York and CUNY Graduate Center, New York, NY 10031, USA email cwolf@ccny.cuny.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 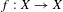$f:X\rightarrow X$ be a continuous dynamical system on a compact metric space 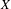$X$ and let 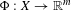$\unicode[STIX]{x1D6F7}:X\rightarrow \mathbb{R}^{m}$ be an 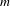$m$-dimensional continuous potential. The (generalized) rotation set 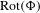$\text{Rot}(\unicode[STIX]{x1D6F7})$ is defined as the set of all $\unicode[STIX]{x1D707}$-integrals of 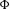$\unicode[STIX]{x1D6F7}$, where $\unicode[STIX]{x1D707}$ runs over all invariant probability measures. Analogous to the classical topological entropy, one can associate the localized entropy 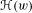$\unicode[STIX]{x210B}(w)$ to each 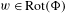$w\in \text{Rot}(\unicode[STIX]{x1D6F7})$. In this paper, we study the computability of rotation sets and localized entropy functions by deriving conditions that imply their computability. Then we apply our results to study the case where 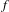$f$ is a subshift of finite type. We prove that 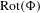$\text{Rot}(\unicode[STIX]{x1D6F7})$ is computable and that 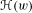$\unicode[STIX]{x210B}(w)$ is computable in the interior of the rotation set. Finally, we construct an explicit example that shows that, in general, 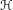$\unicode[STIX]{x210B}$ is not continuous on the boundary of the rotation set when considered as a function of 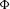$\unicode[STIX]{x1D6F7}$ and 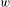$w$. In particular, 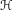$\unicode[STIX]{x210B}$ is, in general, not computable at the boundary of 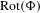$\text{Rot}(\unicode[STIX]{x1D6F7})$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 2 , February 2020 , pp. 367 - 401
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barral, J. and Qu, Y.-H.. On the higher-dimensional multifractal analysis. Discrete Math. Theor. Comput. Sci. 32 (2012), 1977–1995.Google Scholar
Barreira, L. and Godofredo, I.. Multifractal analysis and phase transitions for hyperbolic and parabolic horseshoes. Israel J. Math. 181 (2011), 347–379.Google Scholar
Binder, I., Braverman, M., Rojas, C. and Yampolsky, M.. Computability of Brolin–Lyubich measure. Comm. Math. Phys. 308 (2011), 743–771.Google Scholar
Binder, I., Braverman, M. and Yampolsky, M.. Filled Julia sets with empty interior are computable. Found. Comput. Math. 7 (2007), 405–416.Google Scholar
Bochi, J. and Zhang, Y.. Ergodic optimization of prevalent super-continuous functions. Int. Math. Res. Not. IMRN 19 (2016), 5988–6017.Google Scholar
Bousch, T.. Le poisson n’a pas d’aretes. Ann. Inst. Henri Poincaré Probab. Stat. 36 (2000), 489–508.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Revised edition. Springer, Berlin, 2008, with a preface by David Ruelle, edited by Jean-René Chazottes.Google Scholar
Brattka, V., Hertling, P. and Weihrauch, K.. A tutorial on computable analysis. New Computational Paradigms. Springer, New York, 2008, pp. 425–491.Google Scholar
Braverman, M.. Parabolic Julia sets are polynomial time computable. Nonlinearity 19 (2006), 1383–1401.Google Scholar
Braverman, M. and Yampolsky, M.. Non-computable Julia sets. J. Amer. Math. Soc. 19 (2006), 551–578.Google Scholar
Braverman, M. and Yampolsky, M.. Computability of Julia sets. Mosc. Math. J. 8 (2008), 185–231.Google Scholar
Braverman, M. and Yampolsky, M.. Computability of Julia sets (Algorithms and Computation in Mathematics, 23) . Springer, Berlin, 2009.Google Scholar
Braverman, M. and Yampolsky, M.. Constructing locally connected non-computable Julia sets. Comm. Math. Phys. 291 (2009), 513–532.Google Scholar
Climenhaga, V. and Pesin, Y.. Building thermodynamics for non-uniformly hyperbolic maps. Arnold Math. J. 3(1) (2017), 37–82.Google Scholar
de Berg, M., Cheong, O., van Kreveld, M. and Overmars, M.. Computational Geometry: Algorithms and Applications. Springer, Berlin, 2008.Google Scholar
Dudko, A.. Computability of the Julia set. Nonrecurrent critical orbits. Discrete Contin. Dyn. Syst. 34 (2014), 2751–2778.Google Scholar
Dudko, A. and Yampolsky, M.. Poly-time computability of the Feigenbaum Julia set. Ergod. Th. & Dynam. Sys. 36 (2016), 2441–2462.Google Scholar
Galatolo, S., Hoyrup, M. and Rojas, C.. Dynamics and abstract computability: computing invariant measures. Discrete Contin. Dyn. Syst. 29 (2011), 193–212.Google Scholar
Gale, D., Klee, V. and Rockarfellar, R. T.. Convex functions on convex polytopes. Proc. Amer. Math. Soc. 19 (1968), 867–873.Google Scholar
Gantmacher, F. R.. Matrizenrechnung. II. Spezielle Fragen und Anwendungen (Hochschulbücher für Mathematik, Bd. 37) . VEB Deutscher Verlag der Wissenschaften, Berlin, 1959.Google Scholar
Garibaldi, E. and Lopes, A. O.. Functions for relative maximization. Dyn. Syst. 22 (2007), 511–528.Google Scholar
Gelfert, K. and Kwietniak, D.. On density of ergodic measures and generic points. Ergod. Th. & Dynam. Sys. 38(5) (2018), 1745–1767.Google Scholar
Gelfert, K. and Wolf, C.. On the distribution of periodic orbits. Discrete Contin. Dyn. Syst. 26 (2010), 949–966.Google Scholar
Geller, W. and Misiurewicz, M.. Rotation and entropy. Trans. Amer. Math. Soc. 351 (1999), 2927–2948.Google Scholar
Giulietti, P., Kloeckner, B., Lopes, A. O. and Marcon, D.. The calculus of thermodynamic formalism. J. Eur. Math. Soc. to appear.Google Scholar
Good, C. and Meddaugh, J.. Shifts of finite type as fundamental objects in the theory of shadowing. Preprint, 2017, arXiv:1702.05170 [math.DS].Google Scholar
Hertling, P. and Spandl, C.. Shifts with decidable language and non-computable entropy. Discrete Math. Theor. Comput. Sci. 10 (2008), 75–93.Google Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. 171 (2010), 2011–2038.Google Scholar
Hoyrup, M. and Rojas, C.. Computability of probability measures and Martin–Löf randomness over metric spaces. Inform. and Comput. 207(7) (2009), 830–847.Google Scholar
Hunt, B. and Ott, E.. Controlling chaos using embedded unstable periodic orbits: the problem of optimal periodic orbits. Nonlinear Dynamics, Chaotic and Complex Systems (Zakopane). Cambridge University Press, Cambridge, 1997, pp. 6–23.Google Scholar
Jenkinson, O.. Frequency locking on the boundary of the barycentre set. Exp. Math. 9 (2000), 309–317.Google Scholar
Jenkinson, O.. Geometric barycentres of invariant measures for circle maps. Ergod. Th. & Dynam. Sys. 21(2) (2001), 511–532.Google Scholar
Jenkinson, O.. Rotation, entropy, and equilibrium states. Trans. Amer. Math. Soc. 353 (2001), 3713–3739.Google Scholar
Jenkinson, O.. Ergodic optimization in dynamical systems. Ergod. Th. & Dynam. Sys. (2018), 1–26 published online January 2018.Google Scholar
Jenkinson, O. and Pollicott, M.. Calculating Hausdorff dimensions of Julia sets and Kleinian limit sets. Amer. J. Math. 124 (2002), 495–545.Google Scholar
Jenkinson, O. and Pollicott, M.. Entropy, exponents and invariant densities for hyperbolic systems: dependence and computation. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 365–384.Google Scholar
Kitchens, B.. Symbolic Dynamics: One-sided, Two-sided and Countable State Markov Shifts. Springer, Berlin, 1998.Google Scholar
Kucherenko, T. and Wolf, C.. The geometry and entropy of rotation sets. Israel J. Math. 1999 (2014), 791–829.Google Scholar
Kucherenko, T. and Wolf, C.. Entropy and rotation sets: a toymodel approach. Commun. Contemp. Math. 18 (2016).Google Scholar
Kucherenko, T. and Wolf, C.. Ground states and zero-temperature measures at the boundary of rotation sets. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets and ergodic measures for torus homeomorphisms. Fund. Math. 137 (1991), 45–52.Google Scholar
Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990).Google Scholar
Pavlov, R.. Shifts of finite type with nearly full entropy. Proc. Lond. Math. Soc. 108 (2014), 103–132.Google Scholar
Pavlov, R. and Schraudner, M.. Entropies realizable by block gluing z d shifts of finite type. J. Anal. Math. 126 (2015), 113–174.Google Scholar
Przytycki, F. and Rivera-Letelier, J.. Nice inducing schemes and the thermodynamics of rational maps. Comm. Math. Phys. 301 (2011), 661–707.Google Scholar
Reitsam, T.. Rotation, entropy and equilibrium states. Master’s Thesis, University of Vienna, 2016.Google Scholar
Rettinger, R. and Weihrauch, K.. The computational complexity of some Julia sets. Proc. Thirty-Fifth Annual ACM Sympos. Theory of Computing. ACM, New York, 2003, pp. 177–185.Google Scholar
Rockafellar, R. T.. Convex Analysis. Princeton University Press, New Jersey, 1970.Google Scholar
Rojas, C. and Yampolsky, M.. Computable geometric complex analysis and complex dynamics. Technical Report, 2017, arXiv:1703.06459 [math.CV].Google Scholar
Ruelle, D.. Thermodynamic Formalism: The Mathematical Structures of Equilibrium Statistical Mechanics (Cambridge Mathematical Library) . 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Shamos, M. I.. Computational geometry. PhD Thesis, Yale University, 1978.Google Scholar
Spandl, C.. Computing the topological entropy of shifts. MLQ Math. Log. Q. 53(4–5) (2007), 493–510.Google Scholar
Spandl, C.. Computability of topological pressure for sofic shifts with applications in statistical physics. J. Univ. Comput. Sci. 14 (2008), 876–895.Google Scholar
Turing, A.. On computable numbers, with an application to the entscheidungsproblem. Proc. Lond. Math. Soc. 42 (1936), 230–265.Google Scholar
Urbanski, M. and Wolf, C.. Ergodic theory of parabolic horseshoes. Comm. Math. Phys. 281 (2008), 711–751.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Weihrauch, K.. Computable Analysis: An Introduction (Texts in Theoretical Computer Science. A European Association for Theoretical Computer Science Series) . Springer, Berlin, 2000.Google Scholar
Wielandt, H.. Unzerlegbare, nicht negative Matrizen. Math. Z. 52 (1950), 642–648.Google Scholar
Wolf, C.. A shift map with a discontinuous entropy function. Preprint, 2018, arXiv:1803.02440 [math.DS].Google Scholar
Ziemian, K.. Rotation sets for subshifts of finite type. Fund. Math. 146 (1995), 189–201.Google Scholar