No CrossRef data available.
Article contents
On the entropy of linear factors
Published online by Cambridge University Press: 01 April 2008
Abstract
In general, the entropy 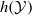 of a stationary process
of a stationary process 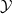 , which is a factor of the process
, which is a factor of the process 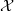 , can take any value in the interval
, can take any value in the interval 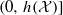 . For linear factors the situation is completely different. In fact it even matters how the class of linear factors is defined. We will investigate both moving averages of bounded sequences by coefficients in l1 and the natural notion in L2.
. For linear factors the situation is completely different. In fact it even matters how the class of linear factors is defined. We will investigate both moving averages of bounded sequences by coefficients in l1 and the natural notion in L2.
Information
- Type
- Research Article
- Information
- Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 697 - 705
- Copyright
- Copyright © Cambridge University Press 2008
References
[1]Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.CrossRefGoogle Scholar
[2]Katznelson, Y.. An Introduction to Harmonic Analysis, 3rd edn. Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
[3]Newman, D. J.. Translates are always dense on the half line. Proc. Amer. Math. Soc. 27 (1969), 511–512.Google Scholar
[4]Parry, W.. Entropy and Generators in Ergodic Theory. W. A. Benjamin, Inc., New York, 1969.Google Scholar
[5]Parry, W.. Topics in Ergodic Theory (Cambridge Tracts in Mathematics, 75). Cambridge University Press, Cambridge, 1981.Google Scholar
[6]Wiener, N.. The Fourier Integral and Certain of its Applications. Cambridge University Press, Cambridge, 1933.Google Scholar

