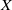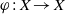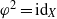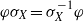Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Béal, Marie-Pierre
Blockelet, Michel
and
Dima, Cǎtǎlin
2016.
Sofic-Dyck shifts.
Theoretical Computer Science,
Vol. 609,
Issue. ,
p.
226.
Nordin, Azmeer
and
Noorani, Mohd Salmi Md
2021.
Counting finite orbits for the flip systems of shifts of finite type.
Discrete & Continuous Dynamical Systems,
Vol. 41,
Issue. 10,
p.
4515.
Nordin, Azmeer
Noorani, Mohd Salmi Md
and
Mohd, Mohd Hafiz
2026.
Orbit counting for sofic shift-flip systems.
Journal of Mathematical Analysis and Applications,
Vol. 555,
Issue. 1,
p.
130021.