No CrossRef data available.
Article contents
On the widths of the Arnol’d tongues
Published online by Cambridge University Press: 03 May 2013
Abstract
Let 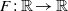 $F: \mathbb{R} \rightarrow \mathbb{R} $ be a real analytic increasing diffeomorphism with
$F: \mathbb{R} \rightarrow \mathbb{R} $ be a real analytic increasing diffeomorphism with 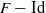 $F- \mathrm{Id} $ being 1-periodic. Consider the translated family of maps
$F- \mathrm{Id} $ being 1-periodic. Consider the translated family of maps 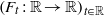 $\mathop{({F}_{t} : \mathbb{R} \rightarrow \mathbb{R} )}\nolimits_{t\in \mathbb{R} } $ defined as
$\mathop{({F}_{t} : \mathbb{R} \rightarrow \mathbb{R} )}\nolimits_{t\in \mathbb{R} } $ defined as 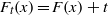 ${F}_{t} (x)= F(x)+ t$. Let
${F}_{t} (x)= F(x)+ t$. Let 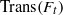 $\mathrm{Trans} ({F}_{t} )$ be the translation number of
$\mathrm{Trans} ({F}_{t} )$ be the translation number of 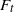 ${F}_{t} $ defined by
${F}_{t} $ defined by 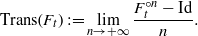 $$\mathrm{Trans} ({F}_{t} ): = \lim _{n\rightarrow + \infty }\frac{{ F}_{t}^{\circ n} - \mathrm{Id} }{n} .$$
$$\mathrm{Trans} ({F}_{t} ): = \lim _{n\rightarrow + \infty }\frac{{ F}_{t}^{\circ n} - \mathrm{Id} }{n} .$$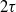 $2\tau $ associated to
$2\tau $ associated to 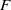 $F$ and let
$F$ and let 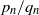 ${p}_{n} / {q}_{n} $ be the
${p}_{n} / {q}_{n} $ be the  $n$th convergent of
$n$th convergent of 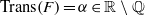 $\mathrm{Trans} (F)= \alpha \in \mathbb{R} \setminus \mathbb{Q} $. Denoting by
$\mathrm{Trans} (F)= \alpha \in \mathbb{R} \setminus \mathbb{Q} $. Denoting by 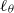 ${\ell }_{\theta } $ the length of the interval
${\ell }_{\theta } $ the length of the interval 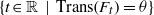 $\{ t\in \mathbb{R} ~\mid ~\mathrm{Trans} ({F}_{t} )= \theta \} $, we prove that the sequence
$\{ t\in \mathbb{R} ~\mid ~\mathrm{Trans} ({F}_{t} )= \theta \} $, we prove that the sequence 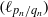 $({\ell }_{{p}_{n} / {q}_{n} } )$ decreases exponentially fast with respect to
$({\ell }_{{p}_{n} / {q}_{n} } )$ decreases exponentially fast with respect to 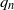 ${q}_{n} $. More precisely,
${q}_{n} $. More precisely, 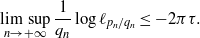 $$\mathop {\mathrm{lim\hphantom{,}sup} }\limits _{n\rightarrow + \infty } \frac{1}{{q}_{n} } \log {\ell }_{{p}_{n} / {q}_{n} } \leq - 2\pi \tau .$$
$$\mathop {\mathrm{lim\hphantom{,}sup} }\limits _{n\rightarrow + \infty } \frac{1}{{q}_{n} } \log {\ell }_{{p}_{n} / {q}_{n} } \leq - 2\pi \tau .$$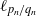 ${\ell }_{{p}_{n} / {q}_{n} } $ and the width of the Arnol’d tongue, which confirms that the widths of the tongues decrease exponentially fast under suitable conditions.
${\ell }_{{p}_{n} / {q}_{n} } $ and the width of the Arnol’d tongue, which confirms that the widths of the tongues decrease exponentially fast under suitable conditions.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Cambridge University Press

