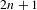Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gaidashev, Denis
and
Yampolsky, Michael
2020.
Renormalization of almost commuting pairs.
Inventiones mathematicae,
Vol. 221,
Issue. 1,
p.
203.
Gaidashev, Denis
and
Gorbovickis, Igors
2021.
Complex a priori bounds for Lorenz maps.
Nonlinearity,
Vol. 34,
Issue. 3,
p.
1263.
Estevez, Gabriela
Smania, Daniel
and
Yampolsky, Michael
2022.
Renormalization of Analytic Multicritical Circle Maps with Bounded Type Rotation Numbers.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 53,
Issue. 3,
p.
1053.
de Faria, Edson
and
Guarino, Pablo
2022.
Dynamics of multicritical circle maps.
São Paulo Journal of Mathematical Sciences,
Vol. 16,
Issue. 1,
p.
340.
Goncharuk, Nataliya
Khanin, Konstantin
and
Kudryashov, Yury
2023.
Circle homeomorphisms with breaks with no $\boldsymbol{C^{2-\nu}}$ conjugacy.
Journal of Modern Dynamics,
Vol. 19,
Issue. 0,
p.
751.
Estevez, Gabriela
and
Guarino, Pablo
2023.
Renormalization of Bicritical Circle Maps.
Arnold Mathematical Journal,
Vol. 9,
Issue. 1,
p.
69.
de Faria, Edson
Guarino, Pablo
and
Nussenzveig, Bruno
2024.
Automorphic measures and invariant distributions for circle dynamics.
Mathematische Zeitschrift,
Vol. 306,
Issue. 2,
Faria, Edson de
and
Guarino, Pablo
2024.
Dynamics of Circle Mappings.
p.
249.
Gorbovickis, Igors
and
Yampolsky, Michael
2025.
Rigidity of analytic and smooth bi-cubic multicritical circle maps with bounded type rotation numbers.
Advances in Mathematics,
Vol. 481,
Issue. ,
p.
110541.
GONCHARUK, NATALIYA
and
YAMPOLSKY, MICHAEL
2025.
Renormalization of circle maps and smoothness of Arnold tongues.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 9,
p.
2845.