No CrossRef data available.
Article contents
Sharp constants in inequalities admitting the Calderón transference principle
Published online by Cambridge University Press: 04 August 2023
Abstract
The aim of this note is twofold. First, we prove an abstract version of the Calderón transference principle for inequalities of admissible type in the general commutative multilinear and multiparameter setting. Such an operation does not increase the constants in the transferred inequalities. Second, we use the last information to study a certain dichotomy arising in problems of finding the best constants in the weak type 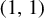 $(1,1)$ and strong type
$(1,1)$ and strong type 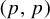 $(p,p)$ inequalities for one-parameter ergodic maximal operators.
$(p,p)$ inequalities for one-parameter ergodic maximal operators.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Bergelson, V. and Leibman, A.. A nilpotent Roth theorem. Invent. Math. 147 (2002), 427–470.10.1007/s002220100179CrossRefGoogle Scholar
Birkhoff, G.. Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA 17 (1931), 656–660.10.1073/pnas.17.2.656CrossRefGoogle ScholarPubMed
Bourgain, J.. On the maximal ergodic theorem for certain subsets of the integers. Israel J. Math. 61 (1988), 39–72.10.1007/BF02776301CrossRefGoogle Scholar
Bourgain, J.. On the pointwise ergodic theorem on
 ${L}^p$
for arithmetic sets. Israel J. Math. 61 (1988), 73–84.10.1007/BF02776302CrossRefGoogle Scholar
${L}^p$
for arithmetic sets. Israel J. Math. 61 (1988), 73–84.10.1007/BF02776302CrossRefGoogle Scholar
Bourgain, J.. Pointwise ergodic theorems for arithmetic sets. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 5–45, with an appendix by the author, H. Furstenberg, Y. Katznelson and D. S. Ornstein.10.1007/BF02698838CrossRefGoogle Scholar
Buczolich, Z. and Mauldin, R.. Divergent square averages. Ann. of Math. (2) 171 (2010), 1479–1530.10.4007/annals.2010.171.1479CrossRefGoogle Scholar
Calderón, A.. Ergodic theory and translation invariant operators. Proc. Natl. Acad. Sci. USA 59 (1968), 349–353.10.1073/pnas.59.2.349CrossRefGoogle ScholarPubMed
Conze, J.-P.. Convergence des moyennes ergodiques pour des sous-suites. Mém. Soc. Math. Fr. (N.S.) 35 (1973), 7–15.Google Scholar
Grafakos, L. and Montgomery-Smith, S.. Best constants for uncentered maximal functions. Bull. Lond. Math. Soc. 29 (1997), 60–64.10.1112/S0024609396002081CrossRefGoogle Scholar
Halmos, P. R.. Lectures on Ergodic Theory. Mathematical Society of Japan, Tokyo, 1956.Google Scholar
Ionescu, A., Magyar, Á., Mirek, M. and Szarek, T. Z.. Polynomial averages and pointwise ergodic theorems on nilpotent groups. Invent. Math. 231 (2023), 1023–1140.10.1007/s00222-022-01159-0CrossRefGoogle Scholar
Jones, R. L., Seeger, A. and Wright, J.. Strong variational and jump inequalities in harmonic analysis. Trans. Amer. Math. Soc. 360 (2008), pp. 6711–6742.10.1090/S0002-9947-08-04538-8CrossRefGoogle Scholar
Kosz, D., Mirek, M., Plewa, P. and Wróbel, B.. Some remarks on dimension-free estimates for the discrete Hardy–Littlewood maximal functions. Israel J. Math. 254 (2023), 1–38.10.1007/s11856-022-2382-7CrossRefGoogle Scholar
Krause, B., Mirek, M. and Tao, T.. Pointwise ergodic theorems for non-conventional bilinear polynomial averages. Ann. of Math. (2) 195 (2022), 997–1109.10.4007/annals.2022.195.3.4CrossRefGoogle Scholar
Lépingle, D.. La variation d’ordre
 $p$
des semi-martingales. Z. Wahrscheinlichkeitstheorie und verw. Gebiete 36 (1976), 295–316.10.1007/BF00532696CrossRefGoogle Scholar
$p$
des semi-martingales. Z. Wahrscheinlichkeitstheorie und verw. Gebiete 36 (1976), 295–316.10.1007/BF00532696CrossRefGoogle Scholar
Melas, A. D.. The best constant for the centered Hardy–Littlewood maximal inequality. Ann. of Math. (2) 157 (2003), 647–688.10.4007/annals.2003.157.647CrossRefGoogle Scholar
Mirek, M., Słomian, W. and Szarek, T. Z.. Some remarks on oscillation inequalities. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2022.77. Published online 29 November 2022.CrossRefGoogle Scholar
Pisier, G. and Xu, Q. H.. The strong
 $p$
-variation of martingales and orthogonal series. Probab. Theory Related Fields 77 (1988), 497–514.10.1007/BF00959613CrossRefGoogle Scholar
$p$
-variation of martingales and orthogonal series. Probab. Theory Related Fields 77 (1988), 497–514.10.1007/BF00959613CrossRefGoogle Scholar
Słomian, W.. Bootstrap methods in bounding discrete Radon operators. J. Funct. Anal. 283 (2022), 109650.10.1016/j.jfa.2022.109650CrossRefGoogle Scholar
Stein, E. M.. On limits of sequences of operators. Ann. of Math. (2) 74 (1961), 140–170.10.2307/1970308CrossRefGoogle Scholar
von Neumann, J.. Proof of the quasi-ergodic hypothesis. Proc. Natl. Acad. Sci. USA 18 (1932), 70–82.10.1073/pnas.18.1.70CrossRefGoogle Scholar


