Some measure rigidity and equidistribution results for β-maps

Abstract

We prove 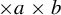$\times a \times b$ measure rigidity for multiplicatively independent pairs when 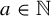$a\in \mathbb {N}$ and 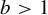$b>1$ is a ‘specified’ real number (the b-expansion of 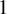$1$ has a tail or bounded runs of 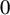$0$s) under a positive entropy condition. This is done by proving a mean decay of the Fourier series of the point masses average along 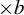$\times b$ orbits. We also prove a quantitative version of this decay under stronger conditions on the 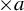$\times a$ invariant measure. The quantitative version together with the 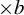$\times b$ invariance of the limit measure is a step toward a general Host-type pointwise equidistribution theorem in which the equidistribution is for Parry measure instead of Lebesgue. We show that finite memory length measures on the a-shift meet the mentioned conditions for mean convergence. Our main proof relies on techniques of Hochman.

1 Introduction

1.1 Definitions and notation

First, we introduce a couple of frequently used definitions. Given a positive real number b, we define the b-fold map $T_{b}:[0,1)\rightarrow [0,1)$ by $T_{b}(x)=b\cdot x\,\mod 1$ . We identify $[0,1)$ with $\mathbb {R}/\mathbb {Z}$ so that $T_{b}$ is referred interchangeably as a toral map that has at most one discontinuity at $0$ . For a real pair $(s,t)\in (1,\infty )\times (1,\infty )$ , we say that they are multiplicatively independent and write $s\nsim t$ if $({\log s}/{\log t})\notin \mathbb {Q}$ . As is customary, we write $[\cdot ],\lceil \cdot \rceil $ for the floor and the ceiling functions, respectively, and $\{ x\} =x-[x]$ for the fractional part of a non-negative real number x.

For a Polish space X, denote by $(X,\Sigma )$ the Borel space that is associated to it. Let $\mu $ be some probability measure on $(X,\Sigma )$ . A sequence of points $\{ x_{n}\} _{n=1}^{\infty }$ in $(X,E)$ is said to be equidistribute for $\mu $ if the mean of their point masses weakly-* converges to $\mu $ : $({1}/{N})\sum _{n=1}^{N}\delta _{x_{n}}\xrightarrow {w-*}\mu $ . Let $T:X\rightarrow X$ be a function. If for some $x\in X$ we have $({1}/{N})\sum _{n=1}^{N}\delta _{T^{n}x}\xrightarrow {w-*}\mu $ , then we say that x equidistributes for $\mu $ under T.

For every $m\in \mathbb {Z}$ and $x\in \mathbb {R}/\mathbb {Z}$ , we write $e_{m}(x)=e(mx)=\exp (2\pi imx)$ . Let $\mu $ be a finite Borel measure on $\mathbb {R}/\mathbb {Z}$ and $M(\mathbb {R}/\mathbb {Z})$ be the set of all such measures. The mth Fourier coefficient of $\mu $ is defined to be $\hat {\mu }(m)=\intop \! e_{m}(x)\,d\mu (x)$ , the Fourier transform of $\mu $ is the sequence $\hat {\mu }=(\hat {\mu }(n))_{n\in \mathbb {Z}}$ and the map $\mathcal {F}:M(\mathbb {R}/\mathbb {Z})\rightarrow \ell ^{\infty }(\mathbb {Z})$ defined by $\mathcal {F}(\mu )=\hat {\mu }$ is the Fourier transform.

We denote the Lebesgue measure on $\mathbb {R}/\mathbb {Z}$ by m and the integration with respect to Lebesgue measure by $dz$ . In our context, all the absolutely continuous measures are with respect to Lebesgue.

1.2 Background

Furstenberg’s Diophantine theorems [3] formed the background to Furstenberg’s pioneering $\times 2 \times 3$ conjecture about the measure rigidity of $T_{2},T_{3}$ . This conjecture suggests that the only non-atomic and ergodic Borel probability measure on the circle which is also $T_{2}$ and $T_{3}$ invariant is Lebesgue measure.

The best result so far on this problem was proved by Rudolph and later strengthened further by Johnson, now known as Rudolph–Johnson theorem [7, 10]. It establishes the conjecture for every multiplicatively independent pair of integers $m,n\geq 2$ under the additional assumption of positive entropy.

Later, the following pointwise ‘equidistributional’ version was proved by Host [6] when $\gcd (a,b)=1$ and improved to the case $a\nsim b$ by Hochman and Shmerkin [5]. Let $\mu $ be a probability measure on $\mathbb {R}/\mathbb {Z}$ which is invariant, ergodic, and has positive entropy with respect to an endomorphism $T_{a}$ . Then $\mu $ -almost every (a.e.) x equidistributes for Lebesgue measure under every endomorphism $T_{b}$ with $a\nsim b$ . We write HET (Host’s equidistribution theorem) for short when referring to this theorem.

In another direction, the next result is due to Parry [9]. Given a real $b>1$ , there exists a unique $T_{b}$ -invariant Borel probability measure that is equivalent to Lebesgue measure. Its Radon–Nikodym derivative can be written explicitly as

$$ \begin{align*} f (x )={ \sum_{x<T_{b}^{n} (1 )}}\frac{1}{b^{n}}\quad\text{and}\quad 1-\frac{1}{b}\leq f\leq\frac{1}{1-{1}/{b}}. \end{align*} $$

Therefore, for an integer $a\geq 2$ and a non-integer $b>1$ , there does not exist a joint $T_{a}$ and $T_{b}$ invariant and absolutely continuous probability measure.

This suggests the following problem.

Problem 1.1. Let $a\geq 2$ be an integer and let $b>1$ be a non-integer such that $a\nsim b$ . Is it true that there are no non-atomic and ergodic Borel probability measures on the circle which are both $T_{a}$ and $T_{b}$ invariant?

The HET and the Parry measure may also be related to each other via the next possible generalization of HET.

Problem 1.2. (Generalized HET)

Let $\mu $ be a probability measure on $\mathbb {R}/\mathbb {Z}$ which is invariant, ergodic, and has positive entropy with respect to an endomorphism $T_{a}$ . Let $1<b\in {\mathbb {R}}$ with $a\nsim b$ . Is it true that $\mu $ -a.e. x equidistributes for Parry measure under $T_{b}$ ?

These two problems are the main concern of this paper.

1.3 Results

We begin by outlining our strategy for tackling Problems 1.1 and 1.2 from a harmonic analysis perspective. We denote the space of bi-infinite sequences both of whose limits are zero by $c_{0}(\mathbb {Z})$ .

In the case of Problem 1.1, a possible strategy is the following.

1. (1) To show that for every probability measure $\mu $ on $\mathbb {R}/\mathbb {Z}$ which is invariant, ergodic, and has positive entropy with respect to an endomorphism $T_{a}$ , it holds that $\mu $ -a.e. x,

   $$ \begin{align*} \bigg\{ \!\intop\!{ \limsup_{N\rightarrow\infty}}\, \bigg|\frac{1}{N}\sum_{i=0}^{N-1}e_{m} (T_{b}^{i} (x ) ) \bigg|\,d\mu \bigg\} _{m=-\infty}^{\infty}\in c_{0} (\mathbb{Z} ). \end{align*} $$

2. (2) Assume by contradiction that $\mu $ is a non-atomic and ergodic Borel probability measure on the circle which is $T_{a}$ - and $T_{b}$ -invariant as in Problem 1.1. Notice that

   $$ \begin{align*} |\hat{\mu} (m ) | & \leq\intop\!{ \limsup_{N\rightarrow\infty}} \,\bigg|\frac{1}{N}\sum_{i=0}^{N-1}e_{m} (T_{b}^{i} (x ) ) \bigg|\,d\mu \end{align*} $$
   and therefore by the first step,
   $$ \begin{align*} \{ |\hat{\mu} (m ) | \} _{m=-\infty}^{\infty}\in c_{0} (\mathbb{Z} ). \end{align*} $$
   However, the $T_{a}$ invariance implies that for every $m\in \mathbb {Z}$ , we have $\hat {\mu }(m)=\hat {\mu }(a\cdot m)$ and the limit above is possible only when
   $$ \begin{align*} \hat{\mu} (m )=\begin{cases} 1 & \text{for }m=0,\\ 0 & \text{for }m\neq0, \end{cases} \end{align*} $$
   that is, when $\mu $ is Lebesgue measure. This contradicts the assumption that $\mu $ is $T_{b}$ -invariant because Lebesgue measure is not $T_{b}$ -invariant.

For the case of Problem 1.2, we will need another definition. Let $a,b$ and $\mu $ be as in Problem 1.2. Given some $x\in [0,1)$ and some subsequence $\{ N_{k}\} $ of $\mathbb {N}$ , we denote $\unicode{x3bb} _{x,\{ N_{k}\} }=\lim _{k\rightarrow \infty }({1}/{N_{k}})\sum _{i=0}^{N_{k}-1}\delta _{T_{b}^{i}(x)}$ , if it exists. It is not hard to show that the only $T_{b}$ -invariant measure with $\ell ^{2}(\mathbb {Z})$ Fourier transform is the Parry measure. Therefore, a possible strategy to solve Problem 1.2 is the following.

1. (1) To show that $\mu $ -a.e. x,

   $$ \begin{align*} \bigg\{ { \limsup_{N\rightarrow\infty}} \,\bigg|\frac{1}{N}\sum_{i=0}^{N-1}e_{m} (T_{b}^{i} (x ) ) \bigg| \bigg\} _{m=-\infty}^{\infty}\in\ell^{2} (\mathbb{Z} ). \end{align*} $$

2. (2) To show that for every $\mu $ -typical x, $\unicode{x3bb} _{x,\{ N_{k}\} }$ is necessarily $T_{b}$ -invariant (for every $\{ N_{k}\} $ such that the limit exists).

3. (3) By the uniqueness of Parry measure, we conclude that it is the limit of every proper convergent subsequence of the sequence

   $$ \begin{align*} \bigg\{ \frac{1}{N}\sum_{i=0}^{N-1}\delta_{T_{b}^{i} (x )} \bigg\} _{N=1}^{\infty} \end{align*} $$
   and we know that such a convergent subsequence does exist. Thus, the whole sequence also converges to Parry measure.

Before stating our first result, we give another definition. Given $1<b\in {\mathbb {R}}$ , there is a non-surjective measurable embedding of $[0,1)$ in $\Lambda _{b}^{\mathbb {N}}=\{ 0,1,\ldots ,[b]-1\} ^{\mathbb {N}}$ which is given by the b-expansion,

$$ \begin{align*} r\mapsto ( [b\cdot r ], [b\cdot T_{b}r ], [b\cdot T_{b}^{2}r ]\ldots ). \end{align*} $$

That is, a subset of $\Lambda _{b}^{\mathbb {N}}$ can represent $[0,1)$ . We say that a real positive b is a specified number or with the specification property if the b-expansion of $1$ has bounded runs of $0$ s or has a tail of $0$ s. The set of specified numbers is uncountable and dense in $(1,\infty )$ (see §2.1). In §3, we prove the following theorem.

Theorem 1.3. Let $\mu $ be a probability measure on $\mathbb {R}/\mathbb {Z}$ which is invariant, ergodic, and has positive entropy with respect to an endomorphism $T_{a}$ for some positive integer $a\geq 2$ and let $b>1$ be a real specified number such that $a\nsim b$ . Then,

$$ \begin{align*} \bigg\{ \!\intop\!{ \limsup_{N\rightarrow\infty}}\, \bigg|\frac{1}{N}\sum_{i=0}^{N-1}e_{m} (T_{b}^{i} (x ) ) \bigg|\,d\mu \bigg\} _{m=-\infty}^{\infty}\in c_{0} (\mathbb{Z} ). \end{align*} $$

According to our strategy, Theorem 1.3 yields a Furstenberg-type measure rigidity for the class of specified b values.

Corollary 1.4. Let $a\geq 2$ be an integer and $b>1$ be a specified non integer such that $a\nsim b$ . Then there are no jointly $T_{a}$ and $T_{b}$ invariant non-atomic and ergodic Borel probability measures with positive entropy under $T_{a}$ .

This is an answer to Problem 1.1 for the class of specified b values under an entropy assumption (the same assumption currently needed when $b\in \mathbb {N}$ ).

To explain our next result, we need a few more definitions. For convenience, we denote $\Lambda _{a}^{-\mathbb {N}}=\Omega ^{-}$ . For an integer $a\geq 2$ , let $\mathcal {A}$ denote the a-adic partition of $[0,1)$ : $\{ [{k}/{a},({k+1})/{a})\} _{k=0}^{a-1}$ and $\mathcal {\mathcal {A}}(x)\in \mathcal {\mathcal {A}}$ denote the element which contains $x\in X$ . Let $\widetilde {\Omega }=\Omega ^{-}\times [0,1)$ be the natural extension of $(\mathbb {R}/\mathbb {Z},\mu ,T_{a})$ together with the map $\widetilde {T}_{a}(\omega ,x)=(\omega \mathcal {A}(x),T_{a}x)$ and write $\widetilde {\mu }$ for the unique extension of $\mu $ to a $\widetilde {T}_{a}$ -invariant measure on $\widetilde {\Omega }$ . Let $\mathcal {C}=\bigvee _{i=-\infty }^{0}{ \widetilde {T}_{a}^{i}\mathcal {A}}$ denote the $\sigma $ -algebra in $\widetilde {\Omega }$ generated by projection to the past: $\widetilde {\omega }=(\omega ,x)\mapsto \omega $ and let $\{ \widetilde {\mu }_{\omega }^{\mathcal {C}}\} _{\omega }$ be the corresponding disintegration. Notice that the members of $\{ \widetilde {\mu }_{\omega }^{\mathcal {C}}\} _{\omega }$ depend only on the $\Omega ^{-}$ -component and that we can identify them as measures on $[0,1)$ such that $\mu =\intop \!\mu _{\omega }\,d\widetilde {\mu }(\omega )$ .

In §4, under stronger assumptions, we prove a quantitative mean version of Theorem 1.3.

Theorem 1.5. Let $a,b,\mu $ be as in Theorem 1.3 and let $\{ I_{j}^{n}\} _{j=1}^{n}$ be the uniform partition of the unit interval into n sub-intervals. Assume that there exists some positive $\alpha $ , such that for every n, the following holds:

$$ \begin{align*} \underset{\eta,j}{\mathop{}\!\mathrm{ess\,sup}}\,\mu_{\eta} (I_{j} )\leq O (n^{-\alpha} ) \end{align*} $$

and such that for some positive $\beta $ , for every positive integer n, we have

$$ \begin{align*} \underset{\eta}{\mathop{}\!\mathrm{ess\,sup}}\iint\chi_{ \{ x: |x-y |<n^{-1} \} }\,d\mu_{\eta} (x )\,d\mu_{\eta} (y )\leq O (n^{-\beta} ). \end{align*} $$

Then for every integer m,

$$ \begin{align*} \textbf{E}_{\mu}\bigg(\limsup_{N} \bigg|\frac{1}{N}\sum_{i=0}^{N-1}e_{m} (T_{b}^{i}x ) \bigg|\bigg)<O ( |m |^{\min_{\gamma,\delta>0}\max \{ -\delta\alpha,({-1-\delta (\alpha-1 )+\gamma\delta})/{2},{\delta (1-\gamma\beta )}/{2} \} } ). \end{align*} $$

We remark that one can always assume $\alpha \le \beta $ (see §4).

In §6.4, we show that the conditions on $\mu $ in Theorem 1.5 are flexible enough to work for every process with memory of finite length such as variable length mixing Markov chains. Nonetheless, it certainly does not always work as we show in §6.3.

Our secondary result from §5 provides the following theorem.

Theorem 1.6. For every real $b>1$ and a $\mu $ -typical x, if $\{ 0\} $ is not an atom of a partial limit $\unicode{x3bb} _{x,\{ N_{k}\} }=\lim _{k\rightarrow \infty }({1}/{N_{k}})\sum _{i=0}^{N_{k}-1}\delta _{T_{b}^{i}}(x)$ , then $\unicode{x3bb} _{x,\{ N_{k}\} }$ must be $T_{b}$ -invariant.

In particular, Theorem 1.3 together with Wiener’s lemma [2] imply that $\{ 0\} $ is not an atom of $\unicode{x3bb} _{x,\{ N_{k}\} }$ , so Theorem 1.6 proves Step 2 in the second strategy under the assumptions of Theorem 1.3.

Notice that since

$$ \begin{align*} -0.5<\min_{\gamma,\delta>0}\max \!\bigg\{ -\!\delta\alpha,\frac{-1-\delta (\alpha-1 )+\gamma\delta}{2},\frac{\delta (1-\gamma\beta )}{2} \bigg\} <0, \end{align*} $$

our strategy fails to solve Problem 1.2. Let us briefly examine some other alternatives. We focused on trying to relax the $\ell ^{2}(\mathbb {Z})$ condition as follows.

Let $L^{1}(m)$ be the set of absolutely continuous measures and let $M_{c}(\mathbb {R}/\mathbb {Z})$ be the set of continuous measures. We say that a measure $\mu $ on $\mathbb {R}/\mathbb {Z}$ is Rajchman if $\lim _{ |n |\rightarrow \infty }{ \hat {\mu }(n)=0}$ and denote the set of Rajchman measures by $\mathcal {R}$ . The Riemman–Lebesgue lemma implies that every absolutely continuous measure is Rajchman. Works by several mathematicians at the beginning of the 20th century (see [8]) established the more extensive result that $L^{1}(m)\subsetneq \mathcal {R}\subsetneq M_{c}(\mathbb {R}/\mathbb {Z})$ . We can naturally ask the following questions. Is it true that Rajchman $T_{b}$ -invariant measure must be absolutely continuous? Equivalently, is it true that $L^{1}(m)\cap \{ T_{b}\text {-invariant}\}=\mathcal {R}\cap \{ T_{b}\text {-invariant}\}$ ? Some evidence for a positive answer comes from the special case of an integer b. In this case, the Parry measure is just the Lebesgue measure and if $\mu $ is $T_{b}$ -invariant and Rajchman, then, as we already observed for every $n\in \mathbb {Z}$ , $\hat {\mu }(T_{b}n)=\hat {\mu }(b\cdot n)$ . Thus, in addition to $\hat {\mu }(0)$ , all the other Fourier coefficients must vanish and $\mu $ is indeed Lebesgue. However, in §7, we show the following proposition.

Proposition 1.7. There exists a $T_{b}$ -invariant Rajchman measure that is not absolutely continuous.

2 Preliminaries

2.1 $\beta $ -shifts

Recall our notation $\Lambda _{b}=\{ 0,1,\ldots ,[b]-1\} $ . With respect to the product $\sigma $ -algebra on $\Lambda _{b}^{\mathbb {N}}$ , the shift transformation $\sigma :\Lambda _{b}^{\mathbb {N}}\rightarrow \Lambda _{b}^{\mathbb {N}}$ which is defined by $\sigma ((\unicode{x3bb} _{i}))=(\unicode{x3bb} _{i+1})$ turns $\Lambda _{b}^{\mathbb {N}}$ into a dynamical system that we call the full $[b]$ shift. The restriction of the full shift to the closure of the subset of sequences which encodes b-expansions is a subshift that we call the b-shift and denote by $X_{b}\subset \Lambda _{b}^{\mathbb {N}}$ .

One says that a real positive b is the following.

• • A simple number if the b-expansion of $1$ has a $0$ s tail.

• • A simple Parry number if the b-expansion of $1$ is a periodic sequence. In some sources, it is also called a (purely) periodic number.

• • A Parry number if the b-expansion of $1$ has a periodic tail. In some sources, it is also called an eventually periodic number.

It is immediate to conclude that

$$ \begin{align*} \{ \text{simple } \#\text{s} \} \subset \{ \text{simple Parry } \#\text{s} \} \subset \{ \text{Parry } \#\text{s} \} \subset \{ \text{specified } \#\text{s} \}. \end{align*} $$

Parry showed [9] that the simple numbers are everywhere dense in $(1,\infty )$ , and so is the set of specified numbers. Schmeling [11] showed that the set of specified numbers also has Hausdorff dimension $1$ , but it is meager and has Lebesgue measure $0$ . In particular, it has the cardinality of the continuum.

An important property of specified numbers is the following proposition.

Proposition 2.1. When b has the specification property, the orbit of $1$ under $T_{b}$ (in $[0,1)$ ) remains bounded away from $0$ unless it hits it.

Proof. Let $1<b\in {\mathbb {R}}$ be a specified number. We write $b_{0}=[b],\ b_{1}=[b\{ b\} ],\ldots $ and similarly we write $r_{0}=T_{b}^{1}(1)=\{ b\} ,\ r_{1}=T_{b}^{2}(1)=\{ b\{ b\} \} ,\ldots. $ We need to prove that $0<\inf _{n}\{ r_{n}:r_{n}>0\} $ . The special case of simple b is trivial. If we assume by contradiction that $0=\inf _{n}\{ r_{n}:r_{n}>0\} $ , then b cannot be simple and there is an upper bound $k\in \mathbb {N}$ on the length of runs of $0$ s. However, for every k, there exists an $n_{0}\in \mathbb {N}$ with $r_{n_{0}}<b^{-(k+1)}$ and therefore $b_{n_{0}+i}=0$ for $1\leq i\leq k+1$ in contradiction.

Finally, we present a result by Parry [9] that gives a criterion to determine whether a given sequence $(b_{n})\in \{ 0,\ldots [b]\} ^{\mathbb {N}}$ is a b-expansion of some $x\in [0,1)$ , $x=b_{0}+{b_{1}}/{\beta }+\cdots $ . We emphasize that there might be many representations of x in this form but only one of them corresponds to the b-expansion that we described earlier. This will be useful for constructing the counterexample in §7.

If $(a_{0},a_{1},\ldots ),(b_{0},b_{1},\ldots )$ are sequences of the same length (finite or infinite) of non-negative integers less than b, we write $(a_{0},a_{1},\ldots )<(b_{0},b_{1},\ldots )$ when $a_{n}<b_{n}$ for the first $a_{n}\neq b_{n}$ .

Theorem 2.2. (Parry’s criterion)

Let $b>1$ be a non-simple number. If the b-expansion of b is $b=a_{0}+{a_{1}}/{b}+\cdots $ and $(b_{0},b_{1},\ldots )$ is a sequence of non-negative integers, a necessary and sufficient condition for the existence of x with b-expansion, $x=b_{0}+{b_{1}}/{b}+\cdots $ , is that $(b_{n},b_{n+1},\ldots )<(a_{0},a_{1},\ldots )$ for all $n\geq 1$ . In particular, $(a_{n},a_{n+1},\ldots )<(a_{0},a_{1},\ldots )$ for all $n\geq 1$ .

2.2 Entropy theory

Let $(X,\mathcal {B})$ be a standard Borel space and $\mathcal {D}\subset \mathcal {B}$ be a measurable partition. We write $\mathcal {\mathcal {D}}(x)\in \mathcal {\mathcal {D}}$ for the element which contains $x\in X$ . This is also well defined when $\mathcal {\mathcal {D}}$ is countably generated $\sigma $ -algebra. In addition, we denote the joining of two finite partitions $\mathcal {A},\mathcal {B}$ by $\mathcal {A\lor \mathcal {B}}=\{ A\cap B:A\in \mathcal {A},B\in \mathcal {B}\} $ . Let $(X,\mathcal {B},\mu )$ be a probability space then the Shannon entropy of $\mu $ with respect to a partition $\mathcal {A}$ of X is the non-negative number $H_{\mu }(A)=-\sum _{A\in \mathcal {A}}\mu (A)\log \mu (A)$ . The entropy $h_{\mu }(T,\mathcal {A})$ of a partition $\mathcal {A}$ of a measure-preserving system $(X,\mathcal {F},\mu ,T)$ is the limit $h_{\mu }(T,\mathcal {A})=\lim _{n\rightarrow \infty }({1}/{n})H_{\mu }(\mathcal {A}_{n})$ , where $\mathcal {A}_{n}={ \bigvee_{i=0}^{n-1}}T^{-i}\mathcal {A}$ . The Kolmagorov–Sinai entropy (or just the entropy) of the m.p.t. $(X,\mathcal {F},\mu ,T)$ is $h_{\mu }(T)=\sup _{\mathcal {A}}h_{\mu }(T,\mathcal {A})$ where the supremum is taken over all the finite partitions $\mathcal {A}$ . Equality is achieved if $\mathcal {A}$ is a generating partition, $\mathcal {F}={ \bigvee _{n=1}^{\infty }}\mathcal {A}_{n}\,\mod \mu $ .

A landmark result in ergodic theory is the Shannon–McMillan–Breiman theorem [14]. Let $(X,\mathcal {F},\mu ,T)$ be an ergodic measure-preserving system and $\mathcal {A}$ a finite partition. Then $\mu $ -a.e. $x \lim _{n\rightarrow \infty }({1}/{n})\log \mu (\mathcal {A}_{n}(x))=h_{\mu }(T,\mathcal {A})$ . It is not hard to deduce from it that an ergodic and $T_{a}$ -invariant Borel probability measure $\mu $ with positive entropy is non-atomic (this also can be proved directly). We will use this corollary in occasional places.

2.3 General results on equidistribution (due to Hochman)

This subsection covers three results that we adopt from Hochman [4]. Two of them are presented with a very superficial description of their proofs to help the reader gain some intuition. A more thorough treatment can be found in the original paper.

We denote the real line translation and scaling maps by

$$ \begin{align*} R_{\theta}x & =x+\theta,\\ S_{t}x & =t\cdot x, \end{align*} $$

respectively. Here $R_{\theta }$ is taken $\mod 1$ when acting on $[0,1)\cong \mathbb {R}/\mathbb {Z}$

Let $\mu $ be a probability measure on $\mathbb {R}/\mathbb {Z}$ and $E\in \mathcal {B}$ such that $\mu (E)>0$ . We write $\mu _{E}=({1}/{\mu (E)})\cdot \mu |_{E}$ for the normalized restriction of $\mu $ to E.

The next technique relates orbits to the local structure of $\mu $ .

Theorem 2.3. [4]

Let $T:X\rightarrow X$ be a continuous map of compact metric space. Let $\mathcal {D}_{1},\mathcal {D}_{2},\ldots $ be a refining sequence of finite Borel partitions. Let $\mu $ be a Borel probability measure on X and assume that $\sup _{n\in \mathbb {N}}\{ \mathop {}\!\mathrm {diam} T_{a}^{n}D:D\in \mathcal {D}_{n+k},\mu (D)>0\} \rightarrow 0$ as $k\rightarrow \infty $ . Then for $\mu $ -a.e. x,

$$ \begin{align*} \bigg(\frac{1}{N}\sum_{n=1}^{N}\delta_{T^{n}x}-\frac{1}{N}\sum_{n=1}^{N}T^{n}\mu_{\mathcal{D}_{n} (x )} \bigg)\xrightarrow[w-*]{N\rightarrow\infty}0. \end{align*} $$

The idea of the proof is to take a countable dense set in $C(X)$ and prove the weak-* convergence with respect to its members. The left average can be replaced with the $\mathcal {D}_{n+k}$ -conditional mean by the assumption. The right average is just the $\mathcal {D}_{n}(x)$ -conditional mean. A variant of the ergodic theorem for martingale differences implies that their limits are equal.

The second theorem is about equidistribution along orbits of the form $(n\theta ,T^{[\beta n]}x)$ , where x is a typical point for $\mu $ .

Theorem 2.4. [4]

Let $(X,\mu ,T)$ be an ergodic m.p.s. on a compact metric space. Let $\beta>0$ and $\theta \neq 0$ . Then for $\mu $ -a.e. x, the sequence $(n\theta ,T^{[\beta n]}x)$ equidistributes for a measure $\nu _{x}$ on $[0,1)\times X$ that satisfies $\intop \!\nu _{x}\,d\mu (x)=\tau \times \mu $ , where $\tau $ is the invariant measure on $([0,1),R_{\theta })$ supported on the orbit closure of $0$ .

The proof uses an intermediate result which says that for $\tau \times \mu $ -a.e. $(u,x)$ , the orbit $(n\theta +u,T^{[\beta n]}x)$ equidistributes for a measure $\nu _{u,x}$ on $[0,1)\times X$ satisfying

$$ \begin{align*} \intop\!\nu_{u,x}\,dz\times d\mu (u,x )=\tau\times\mu. \end{align*} $$

We will not go into its detail besides mentioning that a suspension of height $1$ is used to overcome the integer part issue. Back to the proof of Theorem 2.4, it implies that Lebesgue-a.e. $u\in [0,1)$ and $\mu $ -a.e. x, $\delta _{n\theta +u}\times \delta _{T^{[n\beta ]}x}\xrightarrow {w-*}\nu _{u,x}$ and also that $\intop \!\nu _{u,x}\,dz\times \mu (u,x)=m\times \mu $ . By translation of the first coordinate, we get that $(n\theta ,T^{[\beta n]}x)$ equidistributes for a measure $\nu _{x}$ on $[0,1)\times X$ , where $\nu _{x}=\nu _{x,0}$ , and with Lemma 2.3 from the original paper, we find that $\intop \!\nu _{x}\,d\mu (x)=\tau \times \mu $ .

Lastly, we give a slightly modified version for Hochman’s evaluation of the Fourier transform of scaled measures.

Lemma 2.5. Let $\mu $ be a non-atomic probability measure on ${\mathbb {R}}$ . Then for every $(c,d)\subset {\mathbb {R}}$ and for every $r>0$ and $m\neq 0$ ,

$$ \begin{align*} \intop\nolimits_{0}^{1} |\mathcal{F} ( (S_{b^{z}}\mu )|_{ [c,d ]} ) (m ) |^{2}\,dz\leq\frac{2\mu ( [c,d ] )^{2}}{r\cdot |m |}+\intop\nolimits_{c}^{d}\intop\nolimits_{c}^{d}\chi_{B_{r} (y' )} (y )\,d\mu (y )\,d\mu (y' ), \end{align*} $$

where $B_{r}(x)=\{ y: |x-y |<r\} $ .

Proof. (Based on Hochman’s proof [4]) Using Fubini,

$$ \begin{align*} \intop\nolimits_{0}^{1} |\mathcal{F} ( (S_{b^{z}}\mu )|_{ [c,d ]} ) (m ) |^{2}\,dz & =\intop\nolimits_{0}^{1} \bigg|\intop\nolimits_{c}^{d}e (mb^{z}y )\,d\mu (y ) \bigg|^{2}\,dz\\ & =\intop\nolimits_{0}^{1}\intop\nolimits_{c}^{d}\intop\nolimits_{c}^{d}e (mb^{z}y )\overline{e (mb^{z}y' )}\,d\mu (y )\,d\mu (y' )\,dz\\ & =\intop\nolimits_{0}^{1}\intop\nolimits_{c}^{d}\intop\nolimits_{c}^{d}e (mb^{z} (y-y' ) )\,d\mu (y )\,d\mu (y' )\,dz\\ & =\intop\nolimits_{c}^{d}\intop\nolimits_{c}^{d}\intop\nolimits_{0}^{1}e (mb^{z} (y-y' ) )\,dz\,d\mu (y )\,d\mu (y' ) \end{align*} $$

and then changing of variables $t=b^{z}$ ,

$$ \begin{gather*} \leq\intop\nolimits_{c}^{d} \bigg(\!\intop\nolimits_{ [c,d ]\backslash B_{r} (y' )} \bigg|\intop\nolimits_{1}^{b}\frac{1}{\log (b )t}e (m (y-y' )t )\,dt \bigg|\,d\mu (y )+\intop\nolimits_{B_{r} (y' )\cap [c,d ]}1\,d\mu (y ) \bigg)\,d\mu (y' ). \end{gather*} $$

Finally, using integration by parts for the inner integral in the left summand,

$$ \begin{align*} \leq\frac{2\mu ( [c,d ] )^{2}}{r\cdot |m |}+\intop\nolimits_{c}^{d}\intop\nolimits_{c}^{d}\chi_{B_{r} (y' )} (y )\,d\mu (y )\,d\mu (y' ).\\[-48pt] \end{align*} $$

3 Proof of Theorem 1.3

Let $a,b,\mu $ be as in Theorem 1.3 and denote $\alpha ={\log b}/{\log a}$ . Given a positive integer n, denote $n'=[\alpha n]$ and $z_{n}=\{ \alpha n\} =\alpha n\mod 1$ . That is, $\{ z_{n}\} _{n\in \mathbb {N}}$ is the orbit of $0\in \mathbb {R}/\mathbb {Z}$ under the irrational rotation by $\alpha $ . Recall that $(\widetilde {\Omega },\widetilde {\mu },\widetilde {T}_{a})$ is the natural extension of $(\mathbb {R}/\mathbb {Z},\mu ,T_{a})$ and $\mu =\intop \!\mu _{\omega }\,d\widetilde {\mu }(\omega )$ is the disintegration of $\mu $ given the past.

Recall that $\mathcal {A}$ denotes the a-adic partition of $[0,1)$ : $\{ [{k}/{a},({k+1})/{a})\} _{k=0}^{a-1}$ and correspondingly $\mathcal {A}_{n}=\bigvee _{i=0}^{n-1}T_{a}^{-i}\mathcal {A}$ is the a-adic partition of generation-n: $\{ [{k}/{a^{n}}, ({k+1})/{a^{n}})\} _{k=0}^{a^{n}-1}$ . This simple partition is convenient to work with and it can easily be shown that it is a generator for $T_{a}$ . Naturally, $\mathcal {A}_{n}(x)$ stands for the nth-generation atom which contains x.

Let f be a non-negative piecewise linear function on $[0,1).$ We denote the set of its discontinuities. The minimal jumps oscillation of f is defined by

$$ \begin{align*} \mathop{}\!\mathrm{mjo} (f )=\min_{x\in J} \Big\{\!\lim_{x'\in x^{+}}f (x' )-\lim_{x'\in x^{-}}f (x' ) \Big\}. \end{align*} $$

Recall the notation $r_{0}=T_{b}^{1}(1)=\{ b\} ,\ r_{1}=T_{b}^{2}(1)=\{ b\{ b\} \} ,\ldots .$ Denote $m_{b}={ \inf _{n}}\{ r_{n}:r_{n}>0\} $ . Since b is specified, we have $0<m_{b}\leq 1$ , as shown in Proposition 2.1. Specifically, $\inf _{n}\mathop {}\!\mathrm {mjo}(\{ T_{b}^{n}\} )=m_{b}$ .

Notice that for every $0<\theta <1-a^{-n'}$ , the function $T_{b}^{n}\circ R_{\theta }\circ S_{a^{-n'}}$ is $T_{b}^{n}$ composed on the affine map $R_{\theta }\circ S_{a^{-n'}}(x)=a^{-n'}x+\theta $ of the real line. That is, this composition is $T_{b}^{n}$ stretched horizontally by $a^{n'}$ and translated by $\theta $ . Hence it is a well-defined piecewise linear map with minimal jumps oscillation which is greater or equal to $\mathop {}\!\mathrm {mjo}(T_{b}^{n})$ . In our notation, it means that $\mathop {}\!\mathrm {mjo}\,(T_{b}^{n}\circ R_{\theta }\circ S_{a^{-n'}})\geq m_{b}$ . Notice that $0<a^{-n'}\cdot b^{n}$ ¡a, so $T_{b}^{n}\circ R_{\theta }\circ S_{a^{-n'}}$ also has a uniform slope bounded from above by $0<a$ . These last two properties imply that $T_{b}^{n}\circ R_{\theta }\circ S_{a^{-n'}}$ has at most $ \lceil a/m_{b} \rceil $ discontinuities with a minimal gap of $m_{b}/a$ between them. Thus, for a sufficiently refined uniform partition of the unit interval, each member of the partition contains at most one discontinuity.

Now we turn to prove Theorem 1.3. Fix a $\widetilde {\mu }$ -typical $\omega \in \Omega ^{-}$ and a $\mu _{\omega }$ -typical $x\in [0,1)$ . Thus, we want to show asymptotic decay of the $\widetilde {\mu }$ -expectation of

(3.1) $$ \begin{align} \limsup_{N} \bigg|\frac{1}{N}\sum_{n=1}^{N}e_{m} (T_{b}^{n}x ) \bigg|. \end{align} $$

It holds that $T_{b}^{n}\mathcal {A}_{n'+l}(x)$ has diameter $O(a^{-l})$ under the metric on $[0,1)\cong \mathbb {R}/\mathbb {Z}$ and by Theorem 2.3, we have

$$ \begin{align*} =\limsup_{N} \bigg|\frac{1}{N}\sum_{n=1}^{N}\intop\! e_{m}\,d (T_{b}^{n} (\mu_{\omega} )_{\mathcal{A}_{n'} (x )} ) \bigg|. \end{align*} $$

Recall that $\mathcal {C}=\bigvee _{i=-\infty }^{0}{ \widetilde {T}_{a}^{i}\mathcal {A}}$ denotes the $\sigma $ -algebra in $\widetilde {\Omega }$ generated by projection to the past. Since $\mathcal {C}\vee \mathcal {A}_{n}=\widetilde {T}_{a}^{n}\mathcal {C}$ , we have the equivariance relation $T_{a}^{n}((\mu _{\omega })_{\mathcal {A}_{n}(x)})=\mu _{\widetilde {T}_{a}^{n}(\omega ,x)}$ and also $(\mu _{\omega })_{\mathcal {A}_{n}(x)}=R_{\theta _{\omega ,x,n}}(S_{a^{-n}}\mu _{\widetilde {T}_{a}^{n}(\omega ,x)})$ for some phase $\theta _{\omega ,x,n}$ . This allows us to write

$$ \begin{align*} =\limsup_{N\rightarrow\infty} \bigg|\frac{1}{N}\sum_{n=1}^{N}\intop\! e_{m} (T_{b}^{n}R_{\theta_{\omega,x,n}}S_{a^{-n'}} (y ) )\,d\mu_{\tilde{T}_{a}^{n'} (\omega,x )} \bigg| \end{align*} $$

(3.2) $$ \begin{align} \leq{ \limsup_{N\rightarrow\infty}}\, \frac{1}{N}\sum_{n=1}^{N} \bigg|\intop\! e_{m} (T_{b}^{n}R_{\theta_{\omega,x,n}}S_{a^{-n'}} (y ) )\,d\mu_{\tilde{T}_{a}^{n'} (\omega,x )} \bigg|. \end{align} $$

If we split the integral above into the sum of integrals on the elements of the uniform partition $\{ I_{j}^{k}\} _{j=1}^{k}$ such that $ |I_{j}^{k} |=1/k$ , we get that for every interval $I_{j_{0}}^{k}$ that does not contain a discontinuity, we have

$$ \begin{gather*} \intop\nolimits_{I_{j_{0}}^{k}}e_{m} (T_{b}^{n}R_{\theta_{\omega,x,n}}S_{a^{-n'}} (y ) )\,d\mu_{\tilde{T}_{a}^{n'} (\omega,x )}=\intop\nolimits_{I_{j_{0}}^{k}}e_{m} (a^{z_{n}}y+\theta_{j_{0},\omega,x,n} )\,d\mu_{\tilde{T}_{a}^{n'} (\omega,x )}, \end{gather*} $$

where $\theta _{j_{0},\omega ,x,n}$ is some phase that can be omitted under absolute value. Otherwise, $I_{j_{0}}^{k}$ contains a discontinuity and its measure is less than $\sup _{j}\mu _{\omega }(I_{j}^{k})$ . We take it into account in equation (3.2), denoting $c_{\omega ,k}= \lceil a/m_{b} \rceil \sup _{j}\mu _{\omega }(I_{j}^{k})$ and write

$$ \begin{align*} \leq c_{\omega,k}+{ \limsup_{N\rightarrow\infty}}\, \frac{1}{N}\sum_{n=1}^{N}\sum_{j=1}^{k} \bigg|\intop\nolimits_{I_{j}^{k}}e_{m} (a^{z_{n}}y+\theta_{j,\omega,x,n} )\,d\mu_{\tilde{T}_{a}^{n'} (\omega,x )} \bigg|. \end{align*} $$

Now apply Theorem 2.4, after omitting the phases because of the absolute value, to obtain

(3.3) $$ \begin{align} \leq c_{\omega,k}+\sum_{j=1}^{k}\intop\! \bigg|\intop\nolimits_{I_{j}^{k}}e_{m} (a^{z}y )\,d\mu_{\eta} \bigg|\,d\nu_{\omega,x} (z,\eta ). \end{align} $$

If we integrate both sides of the inequality in equations (3.1) and (3.3) with respect to $\widetilde {\mu }$ , then by Corollary 2.4, it becomes

$$ \begin{align*} &\intop\!\limsup_{N\rightarrow\infty} \bigg|\frac{1}{N}\sum_{n=1}^{m}e_{m} (T_{b}^{n}x ) \bigg|\,d\widetilde{\mu} (\omega,x )\\[5pt]&\quad\leq\intop\!\! \bigg(c_{\omega,k}+\sum_{j=1}^{k}\intop\! \bigg|\intop\nolimits_{I_{j}^{k}}e_{m} (a^{z}y )\,d\mu_{\omega} \bigg| \bigg)\,dz\,d\widetilde{\mu} (\omega,x ). \end{align*} $$

Next, we apply the Cauchy–Schwartz inequality to get

$$ \begin{gather*} \leq\intop\!\! \bigg(c_{\omega,k}+\sqrt{k\sum_{j=1}^{k}\intop\! \bigg|\intop\nolimits_{I_{j}^{k}}e_{m} (a^{z}y )\,d\mu_{\eta} \bigg|^{2}\,dz} \bigg)\,d\widetilde{\mu} (\omega,x ), \end{gather*} $$

where Lemma 2.5 can provide the following evaluation. For any $r>0$ ,

$$ \begin{align*} \leq\intop\!\! \bigg(c_{\omega,k}+\sqrt{\frac{k\sum_{j=1}^{k}\mu_{\eta} (I_{j}^{k} )^{2}}{r |m |}+k\iint\chi_{B_{r} (y )}\,d\mu_{\omega} (y' )\,d\mu_{\omega} (y )} \bigg)\,d\widetilde{\mu} (\omega,x ). \end{align*} $$

Notice that the conditional measures $\mu _{\omega }$ are continuous because $\mu $ was assumed to have positive entropy so by the dominated convergence theorem,

$$ \begin{align*} \intop\! c_{\omega,k}\,d\widetilde{\mu} (\omega,x )= \bigg\lceil \frac{a}{m_{b}} \bigg\rceil \intop\!\sup_{j}\mu_{\omega} (I_{j}^{k} )\,d\widetilde{\mu} (\omega,x )\xrightarrow{k\rightarrow\infty}0 \end{align*} $$

and similarly,

$$ \begin{align*} \textbf{E}_{\mu_{\omega}} (\mu_{\omega} (B_{r} (y ) ) )=\iint\chi_{B_{r} (y )} (y' )\,d\mu_{\omega} (y' )\,d\mu_{\omega} (y )\xrightarrow{r\rightarrow0}0. \end{align*} $$

Finally, we can choose $r= |m |^{-1+\epsilon }$ and $k=\min \{ |m |^{0.5\epsilon },\textbf {E}_{\mu _{\omega }}(\mu _{\omega }(B_{r}(y)))^{-1+\epsilon }\} $ for a small $\epsilon>0$ in a way that

$$ \begin{align*} \intop\! c_{\omega,k}+\sqrt{\frac{k\sum_{j=1}^{k}\mu_{\eta} (I_{j}^{k} )^{2}}{r |m |}+k\textbf{E}_{\mu_{\omega}} (\mu_{\omega} (B_{r} (y ) ) )}\,d\widetilde{\mu} (\omega,x )\xrightarrow{m\rightarrow\infty}0.\\[-41pt] \end{align*} $$

$\square $

4 Proof of Theorem 1.5

The main difference between the previous proof and the quantitative one here is that we assume explicit bounds on $\intop \! c_{\omega ,k}\,d\widetilde {\mu }(\omega ,x)$ and $\textbf {E}_{\mu _{\omega }}(\mu _{\omega }(B_{r}(y)))$ . In addition, we aim for a pointwise decay instead of mean decay. This may be achieved by relating the decay of a stochastic process to the decay of its mean (as in §4.1).

We begin by repeating our assumptions. Let $a,b,\mu $ be as in Theorem 1.3. Denote the uniform partition of the interval $\mathbb {R}/\mathbb {Z}$ into k pieces by $\{ I_{j}^{k}\} _{j=1}^{k}$ such that $ |I_{j}^{k} |=1/k$ and assume that for some $0<\alpha $ and for every $k\in \mathbb {N}$ ,

(4.1) $$ \begin{align} \underset{j,\omega}{\mathop{}\!\mathrm{ess\,sup}}\,\mu_{\omega} (I_{j}^{k} )\leq O (k^{-\alpha} ). \end{align} $$

When this holds, it also imposes a secondary property which is important for us,

$$ \begin{align*} \underset{\eta\in\Omega^{-}}{\mathop{}\!\mathrm{ess\,sup}}\iint\chi_{B_{k^{-1}} (y )} (x )\,d\mu_{\eta} (x )\,d\mu_{\eta} (y ) & \leq O (k^{-\alpha} ), \end{align*} $$

but it is useful to have here a distinct parameter $\beta \geq \alpha $ such that

(4.2) $$ \begin{align} \underset{\eta\in\Omega^{-}}{\mathop{}\!\mathrm{ess\,sup}}\iint\chi_{B_{k^{-1}} (y )} (x )\,d\mu_{\eta} (x )\,d\mu_{\eta} (y )\leq O (k^{-\beta} ). \end{align} $$

The first part of the proof is identical to the previous one but now we think of the limit

$$ \begin{align*} \limsup_{N} \bigg|\frac{1}{N}\sum_{n=1}^{N}e_{m} (T_{b}^{n}x ) \bigg| \end{align*} $$

as a random variable from $\mathbb {R}/\mathbb {Z}$ to ${\mathbb {R}}$ . Again, we fix a $\widetilde {\mu }$ -typical $\omega \in \Omega ^{-}$ and a $\mu _{\omega }$ -typical $x\in [0,1)$ , and consider

$$ \begin{align*} \limsup_{N} \bigg|\frac{1}{N}\sum_{n=1}^{N}e_{m} (T_{b}^{n}x ) \bigg|. \end{align*} $$

We repeat the steps in equations (3.1) to (3.3) from the previous proof up to replace $c_{\omega ,k}$ with $O(k^{-\alpha })$ according to the condition in equation (4.1). That is,

$$ \begin{align*} &\intop\!\limsup_{N} \bigg|\frac{1}{N}\sum_{n=1}^{N}e_{m} (T_{b}^{n}x ) \bigg|\,d\widetilde{\mu} (\omega,x )\\ &\quad\leq\intop\! O (k^{-\alpha} )+\sqrt{k\sum_{j=1}^{k}\intop\! \bigg|\intop\nolimits_{I_{j}^{k}}e_{m} (a^{z}y )\,d\mu_{\eta} \bigg|^{2}\,dz}\,d\widetilde{\mu} (\omega,x ). \end{align*} $$

In this case, Lemma 2.5 can provide the following evaluation. For any $r>0$ , using $ |I_{j}^{k} |=1/k$ and $\mu _{\eta }(I_{j}^{k})\leq O(k^{-\alpha })$ ,

$$ \begin{align*} \leq\intop\! O (k^{-\alpha} )+\sqrt{\frac{O (k^{1-\alpha} )}{r |m |}+k\int\chi_{B_{r}} (y )\,d\mu_{\omega} (y' )\,d\mu_{\omega} (y )}\,d\widetilde{\mu} (\omega,x ). \end{align*} $$

Finally, denote $r=k^{-\gamma }$ and choose $k=[ |m |^{\delta }]$ for some $0<\delta $ . Then with the condition in equation (4.2),

$$ \begin{align*} &\leq\intop\! O ( |m |^{-\delta\alpha} )+\sqrt{O ( |m |^{-1-\delta (\alpha-1 )+\gamma\delta} )+O ( |m |^{\delta (1-\gamma\beta )} )}\,d\widetilde{\mu} (\omega,x )\\ &\leq O ( |m |^{\min_{\gamma,\delta>0}\max \{ -\delta\alpha,({-1-\delta (\alpha-1 )+\gamma\delta})/{2},{\delta (1-\gamma\beta )}/{2} \} } ). \end{align*} $$

Notice that $({-1-\delta (\alpha -1)+\gamma \delta })/{2}\geq -0.5$ , which means that the referred expression in the exponent is bounded from below by $-0.5$ . An upper bound is achieved under the equality $2\delta \alpha =1+\delta (\alpha -1)-\gamma \delta =\gamma \delta \beta -\delta $ that leads to $\gamma =({2\alpha +1})/{\beta }$ and $\delta ={\beta }/({\beta (1+\alpha )+2\alpha +1})$ . Therefore,

$$ \begin{align*} \leq O ( |m |^{- ({\alpha\beta}/({\beta (1+\alpha )+2\alpha+1}) )} ) \end{align*} $$

and the conclusion is that the exponent is strictly bounded between $-0.5$ and $0$ . As already mentioned, this decay rate is too slow for applying our second strategy from the introduction.

We remark that both the conditions in equations (4.1) and (4.2) can be relaxed in several ways and mention here one of them as an example. If the conditions in equations (4.1) and (4.2) hold outside a sequence of measurable sets whose measure decays at some known rate, we still promise the mean decay of the Fourier transform at a rate that we are able to bound.

Lastly, although we did not achieve the desired result, we want to make a suggestion of how to progress further in that direction. This will be relevant if someone manages to improve the evaluation of the decay rate from above.

4.1 Relating the decay rate of a stochastic process to the decay rate of its mean

Let $(X,\mathcal {B},\mu )$ be a probability space and $\{ A_{m}\}_{m=1}^{\infty }$ be a stochastic process. A conventional application of Markov’s inequality and the first Borel–Cantelli lemma implies that the decay rate in m of $\{|A_{m}|\}_{m=1}^{\infty }$ relates to the decay rate in m of its means $\{\textbf {E}_{\mu }(|A_{m}|)\}_{m=1}^{\infty }$ in the following way.

Proposition 4.1. If there exists a real $0<\alpha $ such that $\textbf {E}_{\mu }|A_{m}|<O(m^{-1-\alpha })$ , then for every $0<\epsilon <\alpha $ , almost surely $|A_{m}|\leq o(m^{-\alpha +\epsilon })$ .

Proof. Fix $c>1$ . By Markov’s inequality $\textbf {P}_{\mu }\{ |A_{m} |>({1}/{c})m^{-\alpha +\epsilon }\} <{c\textbf {E}_{\mu }|A_{m}|}/{m^{-\alpha +\epsilon }}$ and from the hypothesis above, there exists some $s>0$ such that $\textbf {P}_{\mu }\{ |A_{m} |>({1}/{c})m^{-\alpha +\epsilon }\} <{(c\cdot s\cdot m^{-1-\alpha })}/{m^{-\alpha +\epsilon }}$ . Thus,

$$ \begin{align*} &\textbf{P}_{\mu} \bigg\{ |A_{m} |>\frac{1}{c}m^{-\alpha+\epsilon} \bigg\} <\frac{c\cdot s\cdot m^{-1-\alpha}}{m^{-\alpha+\epsilon}}=c\cdot s\cdot m^{-1-\epsilon}\\ &\quad\implies\sum_{m}\textbf{P}_{\mu} \bigg\{ |A_{m} |>\frac{1}{c}m^{-\alpha+\epsilon} \bigg\} <\infty. \end{align*} $$

Finally, by the first Borel–Cantelli lemma, $\textbf {P}_{\mu }(\limsup _{m}\{|A_{m}|>({1}/{c})m^{-\alpha +\epsilon }\})=0$ , which implies that $\{|A_{m}|>({1}/{c})m^{-\alpha +\epsilon }\}$ occur finitely often with probability $1$ .

5 Proof of Theorem 1.6

We begin with providing an equivalent definition of weak-* convergence that will be needed in that section, via the next continuous mapping theorem (see [1, Theorem 2.57]).

Theorem 5.1. $\mu _{n}\xrightarrow {w-*}\mu $ if and only if $\intop \! f\,d\mu _{n}\xrightarrow {n\rightarrow \infty }\intop \! f\,d\mu $ for every bounded function $f:X\rightarrow \mathbb {{\mathbb {R}}}$ with $\mu (\{ x:f\text { has a discontinuity at }x\} )=0$ .

Let x be a $\mu $ -typical point. In this part, we assume that x equidistributes along a subsequence $\{ N_{k}\} $ under $T_{b}$ for some measure where all the hypotheses are as in Problem 1.2 and also that $\{ 0\} $ is not an atom of this measure. Recall that in our notation, it means that the limit $\unicode{x3bb} _{x,\{ N_{k}\} }=\lim _{k\rightarrow \infty }({1}/{N_{k}})\sum _{i=0}^{N_{k}-1}\delta _{T_{b}^{i}(x)}$ is well defined. Then we show that $\unicode{x3bb} _{x,\{ N_{k}\} }$ must be $T_{b}$ -invariant. For convenience, our proof is given as if the equidistribution is along the whole sequence since for equidistribution along a subsequence, the argument is identical. Here we denote the limit measure by $\unicode{x3bb} _{\infty }$ for short.

Fix $1<b\in {\mathbb {R}}$ and let $x\in \mathbb {R}/\mathbb {Z}$ be a $\mu $ -typical point and denote

$$ \begin{gather*} \unicode{x3bb}_{N}=\frac{1}{N}\sum_{i=0}^{N-1}\delta_{T_{b}^{i}x}\xrightarrow{w-*}\lim_{N\rightarrow\infty}\frac{1}{N}\sum_{i=0}^{N-1}\delta_{T_{b}^{i}x}=\unicode{x3bb}_{\infty}. \end{gather*} $$

We need to show that

$$ \begin{align*} \intop\! f\,d\unicode{x3bb}_{\infty}=\intop\! f\,dT_{b*}\unicode{x3bb}_{\infty} \end{align*} $$

for all $f\in C(\mathbb {R}/\mathbb {Z})$ .

We have

$$ \begin{align*} \unicode{x3bb}_{N}-T_{b*}\unicode{x3bb}_{N}=\frac{1}{N}\sum_{i=0}^{N-1}\delta_{T_{b}^{i} (x )}-\frac{1}{N}\sum_{i=0}^{N-1}\delta_{T_{b}^{i+1} (x )}=\frac{\delta_{x}-\delta_{T_{b}^{N} (x )}}{N}\xrightarrow{N\rightarrow\infty}0, \end{align*} $$

so $\lim _{N\rightarrow \infty }(\unicode{x3bb} _{N}-T_{b*}\unicode{x3bb} _{N})=0$ .

Additionally, for every $f\in C(\mathbb {R}/\mathbb {Z})$ , $f\circ T_{b}$ has at most one discontinuity which is located at $0$ and by assumption, $\unicode{x3bb} _{\infty }(\{ 0\} )=0$ . Since $\unicode{x3bb} _{N}\xrightarrow {w-*}\unicode{x3bb} _{\infty }$ for any $f\in C(\mathbb {R}/\mathbb {Z})$ , then by Theorem 5.1,

$$ \begin{gather*} \textbf{E}_{T_{b*}\unicode{x3bb}_{N}} (f )=\textbf{E}_{\unicode{x3bb}_{N}} (f\circ T_{b} )\xrightarrow{N\rightarrow\infty}\textbf{E}_{\unicode{x3bb}_{\infty}} (f\circ T_{b} )=\textbf{E}_{T_{b*}\unicode{x3bb}_{\infty}} (f ). \end{gather*} $$

Now we can stitch it all together and get for every $f\in C(\mathbb {R}/\mathbb {Z})$ that

$$ \begin{align*} |\textbf{E}_{\unicode{x3bb}_{\infty}} (f )-\textbf{E}_{T_{b*}\unicode{x3bb}_{\infty}} (f ) |\leq & |\textbf{E}_{\unicode{x3bb}_{\infty}} (f )-\textbf{E}_{\unicode{x3bb}_{N}} (f ) |\\ &+ |\textbf{E}_{\unicode{x3bb}_{N}} (f )-\textbf{E}_{T_{b*}\unicode{x3bb}_{N}} (f ) |\\ &+ |\textbf{E}_{T_{b*}\unicode{x3bb}_{N}} (f )-\textbf{E}_{T_{b*}\unicode{x3bb}_{\infty}} (f ) |\rightarrow0 \end{align*} $$

as N tends to infinity which implies the desired result.

6 Exploring conditions in equations (4.1) and (4.2)

In this section, we inquire the validity range of conditions in equations (4.1) and (4.2). We added some brief theoretical background that will be used for that subjective.

6.1 Stationary coding

The content of this subsection is taken from the book of P. Shields on ergodic theory [12].

Let A and B be finite sets. A Borel measurable map $F:A^{\mathbb {Z}}\rightarrow B^{\mathbb {Z}}$ is a stationary coder if $F(T_{A}x)=T_{B}F(x)$ for every $x\in A^{\mathbb {Z}}$ , where $T_{A}$ and $T_{B}$ denote the shifts on the respective two-sided sequence spaces $A^{\mathbb {Z}}$ and $B^{\mathbb {Z}}$ . Stationary coding carries a Borel measure $\mu $ on $A^{\mathbb {Z}}$ into the measure $\nu =\mu \circ F^{-1}$ defined for Borel subsets C of $B^{\mathbb {Z}}$ by $\nu (C)=\mu (F^{-1}(C))$ . The encoded process $\nu $ is said to be a stationary coding of $\mu $ , with coder F. It is immediate to conclude that a stationary coding of a stationary process is itself a stationary process.

The map $f:A^{\mathbb {Z}}\rightarrow B$ defined by the formula $f(x)=F(x)_{0}$ is the time-zero coder associated with F. Notice that stationary coding preserves ergodicity.

Let T be an invertible, ergodic transformation of the probability space $(X,\Sigma ,\mu )$ . Let S be a set of positive measure. Denote by $\{ R_{n}\} $ the $(T,\mathcal {A}_{S})$ -process defined by the partition $\mathcal {A}_{S}=\{ S,X\setminus S\} $ with $X\setminus S$ labeled by $0$ and S labeled by $1$ . That is, $R_{n}(x)=\chi _{S}(T^{n}x)$ for every integer $n\in \mathbb {Z}$ . Notice that $\{ R_{n}\} $ is a stationary coding of the $(T,\mathcal {A}_{S})$ -process with time zero coder $\chi _{S}$ and therefore it is ergodic.

Notice that such a non-trivial $\{ R_{n}\} $ process (i.e $0<\mu (S)<1$ ) has positive entropy where $(X,\Sigma ,\mu )$ is a product measure on $\mathcal {A}_{S}^{\mathbb {Z}}$ . This is because a non-trivial $(T,\{ S,X\setminus S\} )$ -process is a factor of Bernoulli measure which has completely positive entropy.

6.2 Reverse Markov’s inequality

The next reverse version of Markov’s inequality is famous and easy to prove. We present it here with a proof for completeness.

Theorem 6.1. (Reverse Markov’s inequality)

Let X be a random variable on a probability space $(\Omega ,\textbf {P})$ that satisfies $\textbf {P}(X\leq a)=1$ for some constant a. Then, for $d<\textbf {E}(X)$ ,

$$ \begin{align*} \textbf{P} (X>d )\geq\frac{\textbf{E}(X)-d}{a-d}. \end{align*} $$

Proof. Define the random variable $V=a-X$ which is almost surely non-negative by assumption. The event $\{ X\leq d\} $ is equivalent to the event $\{ V\geq a-d\} $ . Now with Markov’s inequality,

$$ \begin{align*} \textbf{P} ( \{ X\leq d \} )=\textbf{P} ( \{ V\geq a-d \} )\leq\frac{\textbf{E}(V)}{a-d}=\frac{a-\textbf{E}(X)}{a-d}, \end{align*} $$

where the right-hand side numerator and denominator are strictly positive since $d<\textbf {E}(X)\leq a$ . Finally,

$$ \begin{align*} \textbf{P} ( \{ X>d \} )=1-\textbf{P} ( \{ X\leq d \} )>\frac{\textbf{E}(X)-d}{a-d}.\\[-41pt] \end{align*} $$

6.3 Not all the $\mu $ values meet the condition in equation (4.2)

Here we construct a counterexample which violates the weaker condition in equation (4.2). We anticipate that the condition in equation (4.1) can be violated by simpler examples.

We use the formalism from §§2.2 and 6.1. Let $(X_{l},\Sigma ,\nu ,\sigma )$ be a uniformly distributed full Bernoulli shift in $2<l$ symbols. We define a measurable set $\mathcal {Y}\in \Sigma $ recursively.

Fix $0<\epsilon <0.5$ . For $k=1$ , fix $2\leq n_{1}\in \mathbb {N}$ such that $\log (n_{1})^{-1}<1-\epsilon $ and let $Y_{1}$ be a set such that $0.5\log (n_{1})^{-2}<\nu (Y_{1})<\log (n_{1})^{-2}$ . Define $\mathcal {Y}_{1}=\bigcup _{m=0}^{[\log n_{1}]}\sigma ^{-m}Y_{1}$ so that $0<\nu (\mathcal {Y}_{1})\leq \log (n_{1})^{-1}$ and also $\nu (\mathcal {Y}_{1})<1-\epsilon $ .

For $1<k\in \mathbb {N}$ , choose $n_{k-1}<n_{k}\in \mathbb {N}$ such that $\log (n_{k})^{-1}<1-\epsilon -\sum _{i=1}^{k-1}\nu (\mathcal {Y}_{i})$ and let $Y_{k}$ be a set such that $0.5\cdot \log (n_{k})^{-2}<\nu (Y_{k})<\log (n_{k})^{-2}$ . Define $\mathcal {Y}_{k}=\bigcup _{m=0}^{[\log n_{k}]}\sigma ^{-m}Y_{k}$ so that $0<\nu (\mathcal {Y}_{k})\leq {1}/{\log n_{k}}\leq 1-\epsilon -\sum _{i=1}^{k-1}\nu (\mathcal {Y}_{i})$ and therefore $0<\sum _{i=1}^{k}\nu (\mathcal {Y}_{i})<1-\epsilon $ .

Finally, define $\mathcal {Y}=\bigcup _{i=1}^{\infty }\mathcal {Y}_{i}$ and define a process on $\{ 0,1\} ^{\mathbb {Z}}$ by $R_{n}(x)=\chi _{\mathcal {Y}}(\sigma ^{n-1}x)$ with the induced measure $\widetilde {\mu }=\nu \circ R^{-1}$ as in §6.1. By our construction, $0<\nu (\mathcal {Y})<1-\epsilon $ and $\{ n_{k}\} $ is strictly increasing. Since $(X_{l},\Sigma ,\nu )$ is ergodic, so is $\{ R_{n}\} $ as a stationary coding with time zero coder (which trivially also preserves the measure). That is, we can interpret $\widetilde {\mu }$ as a probability measure which is ergodic and shift invariant on the binary full shift. It also has positive entropy by §6.1.

In another direction, notice that $[0,1)$ is the image of the infinite binary sequences $\{ 0,1\} ^{\mathbb {N}}$ under the natural map $(x_{i})_{i=1}^{\infty }\mapsto \sum _{i=1}^{\infty }({x_{i}}/{2^{i}})$ which is also a bijection on the complement of a countable set, that is, a bijection on the complement of a null set for every continuous measure. Thus, if we denote $X_{2}=\{ 0,1\} ^{\mathbb {Z}}$ (the 2-shift), then we can define up to a null set the bijection $\iota :X_{2}\rightarrow \{ 0,1\} ^{-\mathbb {N}_{0}}\times [0,1)$ . We can also define the pushforward $\widetilde {\rho }=\widetilde {\mu }\circ \iota ^{-1}$ (that is, a measure on $\{ 0,1\} ^{-\mathbb {N}_{0}}\times [0,1)$ ) which preserves all the relevant properties of $\widetilde {\mu }$ (ergodicity is trivial and positive entropy by being a non-trivial factor of the system with completely positive entropy). Now, $\widetilde {\rho }=\intop \!\rho _{\eta }\,d\widetilde {\rho }(\eta )$ , where it is disintegrated with respect to the $\sigma $ -algebra that is generated by projection to the past (like in §1.3) and the conditional measures $\rho _{\eta }$ identified as measures on $[0,1)$ . Similarly, $\widetilde {\mu }=\intop \! d\mu {}_{\eta }\,d\widetilde {\mu }(\eta )$ , where $\eta \in \{ 0,1\} ^{-\mathbb {N}_{0}}$ .

For every $k\in \mathbb {N}$ , denote the event $\bigcap _{i=0}^{[\log n_{k}]}\{ R_{i}=1\}$ by $E_{k}$ . We begin with

$$ \begin{align*} {\intop\!\iint\chi_{B_{n_{k}^{-1}}(y)}(x)\,d\rho_{\eta}(x)\,d\rho_{\eta}(y)\,d\widetilde{\rho}(\eta)}, \end{align*} $$

where $B_{n_{k}^{-1}}(y)=\{ x\in [0,1): |x-y |<n_{k}^{-1}\} $ . We need to show that this integral decays in $n_{k}$ with sub polynomial rate. We can pullback this integration to the space $X_{2}$ and restrict it to the event $E_{k}\times E_{k}$ since every pair $(x',y')\in E_{k}\times E_{k}$ corresponds to a pair $(x,y)\in [0,1)^{2}$ with $ |x-y |<{1}/{n_{k}}$ . Thus,

$$ \begin{align*}& \geq\intop\!\intop\!\!\!\intop\chi_{E_{k}\times E_{k}} (x,y )\,d\mu_{\eta}\times\mu_{\eta} (x,y )\,d\widetilde{\mu} (\eta )\\& =\intop\!\intop\!\chi_{E_{k}} (x )\,d\mu{}_{\eta} (x )\intop\!\chi_{E_{k}} (y )\,d\mu_{\eta} (y )\,d\widetilde{\mu} (\eta )\\& =\intop\!\! \bigg(\!\intop\!\chi_{E_{k}} (x )\,d\mu{}_{\eta} (x ) \bigg)^{2}\,d\widetilde{\mu} (\eta )\\& \geq \bigg(\!\intop\!\intop\!\chi_{E_{k}} (x )\,d\mu{}_{\eta} (x )\,d\widetilde{\mu} (\eta ) \bigg)^{2}\\& = \bigg(\!\intop\!\chi_{E_{k}} (x )\,d\widetilde{\mu} (x ) \bigg)^{2},\end{align*} $$

where in the first equality, we used Fubini and then split the integral into two separate integrals, and the second inequality is Jensen. We can pullback the integration once again to the full shift $X_{l}$ and restrict it to the event $Y_{k}$ which included in the preimage of $E_{k}$ ,

$$ \begin{align*} & \geq \bigg(\!\intop\!\chi_{Y_{k}} (x)\,d\nu (x ) \bigg)^{2}\\ & =0.25\cdot\log(n_{k})^{-4}. \end{align*} $$

Now, for every $k\in \mathbb {N}$ , we can use the reverse Markov inequality (Theorem 6.1) with $a=2$ and $d={1}/{8\log (n_{k})^{4}}$ to get

$$ \begin{align*} \textbf{P}_{\widetilde{\mu}} \bigg(\bigg\{\intop\!\mu{}_{\eta} (B_{n_{k}^{-1}} (y ) )\,d\mu{}_{\eta} (y )\geq\frac{1}{8\log (n_{k} )^{4}}\bigg\} \bigg)\geq\frac{1}{16\log (n_{k} )^{4}}. \end{align*} $$

This violates the condition in equation (4.2).

6.4 Processes with memory of finite length meet the condition in equation (4.1)

In this special case, it will be enough to use the total probability formula to reach the condition in equation (4.1) which also implies that the condition in equation (4.2) holds.

Let A be a finite alphabet $ |A |=l$ for some integer $l\geq 2$ and let $(A^{\mathbb {Z}},\mu ,T)$ be a finite memory length symbolic process which is ergodic, invariant, and with positive entropy with respect to T. That is, the prediction of $A_{0}$ depends only on a finite portion of the past $A_{-n},\ldots ,A_{-1}$ for some $n<\infty $ or explicitly for every $m\in \mathbb {Z}$ and $x\in A^{\mathbb {Z}}$ , $\mu ([x_{m+n}^{\infty }]|[x_{-\infty }^{m}])=\mu ([x_{m+n}^{\infty }])$ . Denote $s=\max _{a\in A}\mu ([a])<1$ . Assume that $n<m$ , then with direct computation,

$$ \begin{align*} \mu_{ [x_{-\infty}^{0} ]} ( [x_{0}^{m} ] ) & \leq\mu ( [x_{n}^{m} ] )\\ & =\mu ( [x_{n} ] )\mu ( [x_{n+1}^{m} ]| [x_{n} ] )\\& \leq\mu ( [x_{n} ] )\mu ( [x_{2n}^{m} ] )\\ & \vdots\\ & =\prod_{i=1}^{[m/n]}\mu ( [x_{n\cdot i} ] )\\ & \leq s^{m/n+1}. \end{align*} $$

If we consider a uniform partition of the unit interval $\{ I_{j}^{k}\} _{j=1}^{k}$ such that $ |I_{j}^{k} |={1}/{k}$ and where $k=l^{m}$ , then the display above implies that $\mathop {}\!\mathrm {ess\,sup}_{j,\omega }\mu _{\omega }(I_{j}^{k})\leq O(k^{\log (s)/(n\log (l))})$ .

7 Rajchman and invariance does not force uniqueness

7.1 Self-similarity and classes of algebraic numbers

Here we set out some of the basic definitions regarding self similarity. A set $\mathcal {F}=\{ f_{1},\ldots f_{k}\} $ for $k\geq 2$ of contractions on ${\mathbb {R}}$ , $f_{i}(x)=r_{i}x+a_{i}$ , with $0<r_{i}<1$ for each $i\in \{ 1,\ldots ,k\} $ , is an iterated function system or IFS for short. We also call the $f_{i}$ terms similarities.

A key fact in this topic is that there exists a unique non-empty compact set $K\subset {\mathbb {R}}$ such that $K=\bigcup _{i=1}^{k}f_{i}(K)$ . We call it the attractor or the self-similar set of the IFS $\mathcal {F}$ .

Given a list of positive numbers $\boldsymbol {p}=(p_{1},\ldots ,p_{k})$ with $\sum _{i=1}^{k}p_{i}=1$ , we call it a positive probability vector and there is a unique probability measure $\mu _{\boldsymbol {p}}$ with $\mu _{\boldsymbol {p}}=\sum _{i=1}^{k}p_{i}\cdot f_{i}\mu _{\boldsymbol {p}}$ . This measure is supported on the attractor of $\mathcal {F}$ and called a self-similar measure.

A Pisot number is a real algebraic integer greater than $1$ all of whose Galois conjugates are less than $1$ in absolute value. A Salem number is a real algebraic integer greater than $1$ whose all conjugate roots have absolute value no greater than $1$ , and at least one of them has an absolute value which equals $1$ . There are countably many Pisot and Salem numbers.

We conclude this part with a recent theorem of Varjú and Yu [13] which plays a major role in our proof that $T_{b}$ -invariant Rajchman measure need not be Parry.

Theorem 7.1. Let $k\geq 2$ be an integer. Let $r_{1}=r^{l_{1}},\ldots ,r_{k}=r^{l_{k}}$ for some $r\in (0,1)$ and $l_{1},\ldots ,l_{k}\in \mathbb {Z}_{>0}$ with $\mathop{\mathrm{gcd}} (l_{1},\ldots ,l_{k})=1$ . Assume that $r^{-1}$ is not a Pisot or Salem number. Let $\mu $ be a non-singleton self-similar measure associated to the IFS $\mathcal {F}=\{ f_{1},\ldots ,f_{k}\} $ ( $f_{i}(x)=r_{i}x+a_{i}$ ) and a positive probability measure. Then,

$$ \begin{align*} |\hat{\mu} (z ) |=O ( |\log (z )^{-c} | ) \end{align*} $$

for some $c>0.$

We use Theorem 7.1 to prove that a Rajchman $T_{b}$ -invariant measure must not be unique. Let $b\geq 2$ be a specified non-simple number which is not Salem or Pisot. We can guarantee the existence of such a number by cardinality considerations (recall that Pisot numbers as well as Salem numbers and simple numbers are countable while specified numbers have the cardinality of continuum).

Denote $\mathbb {N}_{0}=\mathbb {N}\cup \{ 0\} $ for short and denote the b-expansion of b by $(a_{i})$ . That is, $b=a_{0}+{a_{1}}/{b}+\cdots $ and in particular $a_{0}=[b]$ . Every sequence $(x_{i})\in \{ 0,1\} ^{\mathbb {N}_{0}}$ and $n\in \mathbb {N}$ satisfies $(x_{i+n})<(a_{i})$ since $x_{n}\in \{ 0,1\} $ which is either way less than $[b]=a_{0}$ . Recall that $X_{b}\subset \Lambda _{b}^{\mathbb {N}_{0}}$ is the subset of sequences that encodes b-expansions, so by Parry’s criterion (Theorem 2.2), we get that $\{ 0,1\} ^{\mathbb {N}_{0}}\subset X_{b}$ .

Define the set $K=\{ \sum _{i=0}^{\infty }({b_{i}}/{b^{i}}):(b_{i})\in \{ 0,1\} ^{\mathbb {N}_{0}}\} $ which is the image of $\{ 0,1\} ^{\mathbb {N}}$ under the b-expansion and define the IFS $\mathcal {F}=\{ f_{0}(x)={x}/{b},f_{1}(x)={x}/{b}+{1}/{b}\} $ . If we denote concatenation of symbols by $\centerdot $ , then clearly $\{ 0,1\} ^{\mathbb {N}_{0}}=0\centerdot \{ 0,1\} ^{\mathbb {N}_{0}}\cup 1\centerdot \{ 0,1\} ^{\mathbb {N}_{0}}$ , which means under the b-expansion, $K=\bigcup _{i=0}^{1}f_{i}(K)$ . Thus, K is the attractor of $\mathcal {F}$ and for every positive probability vector $\boldsymbol {p}=(p_{0},p_{1})$ , the self-similar measure that satisfies $\mu _{\boldsymbol {p}}=\sum _{i=0}^{1}p_{i}\cdot f_{i}\mu _{\boldsymbol {p}}$ is well defined. Pulling it back again under the b-expansion, it translated into a Bernoulli shift $\boldsymbol {p}^{\mathbb {N}_{0}}$ on $X_{b}|_{\{ 0,1\} ^{\mathbb {N}_{0}}}=\{ 0,1\} ^{\mathbb {N}_{0}}$ , where the former is $T_{b}$ -invariant and correspondingly the latter is shift invariant.

If we consider Theorem 7.1 where both of the $l_{i}$ terms are equal to $1$ such that $\mathrm{gcd}(l_{0},l_{1})=1$ , then all the hypotheses hold with respect to b and $\mathcal {F}$ and any self-similar measure $\mu _{\boldsymbol {p}}$ provides the Rajchman property,

$$ \begin{align*} |\hat{\mu}_{\boldsymbol{p}} (z ) |=O ( |\log (z )^{-c} | ). \end{align*} $$

Since there are infinitely many of them, the uniqueness is violated.