No CrossRef data available.
Article contents
Spatial determinism for a free Z2-action
Published online by Cambridge University Press: 16 December 2011
Abstract
We extend the idea of bilateral determinism of a free Z-action by D. Ornstein and B. Weiss to a free Z2-action. We show that we have a ‘stronger’ spatial determinism for Z2-actions: to determine the complete Z2-name of a point, it is enough to know the name of a fraction of the orbit whose density can be made arbitrarily small. Moreover, for zero-entropy Z2-actions, we prove that there exists a partition 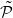 such that the
such that the 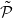 -names of an arbitrarily small one-sided cone determine the points.
-names of an arbitrarily small one-sided cone determine the points.
Information
- Type
- Research Article
- Information
- Ergodic Theory and Dynamical Systems , Volume 32 , Issue 2: Daniel J. Rudolph – in Memoriam , April 2012 , pp. 479 - 489
- Copyright
- Copyright © Cambridge University Press 2011
References
[1]Burton, R.. An asymptotic definition of K-groups of automorphisms and a non-Bernoullian counter-example. Z. Wahr. verw. Geb. 47 (1979), 205–212.CrossRefGoogle Scholar
[2]Burton, R. and Steif, J.. Coupling surfaces and weak Bernoulli in one and higher dimensions. Adv. Math. 132(1) (1997), 1–23.Google Scholar
[3]Conze, J. P.. Entropie d’un groupe abelien de transformations. Z. Wahr. verw. Geb. 25 (1972), 11–30.Google Scholar
[4]Dou, D., Hwang, W. and Park, K. K.. Entropy dimension of topological dynamical systems. Trans. Amer. Math. Soc. 363 (2011), 659–680.CrossRefGoogle Scholar
[5]Dou, D., Hwang, W. and Park, K. K.. Entropy dimension of measure preserving systems. Preprint.Google Scholar
[6]Ferenczi, S. and Park, K.. Entropy dimensions and a class of constructive examples. J. Contin. Discrete Dyn. Syst. 17 (2007), 133–141.Google Scholar
[7]Krieger, W.. On the entropy and generators of measure preserving transformations. Trans. Amer. Math. Soc. 149 (1970), 453–464.CrossRefGoogle Scholar
[8]Ornstein, D. and Weiss, B.. Every transformation is bilaterally deterministic. Israel J. Math. 21 (1975), 154–158.Google Scholar
[9]Ornstein, D. and Weiss, B.. Entropy and isomorphism theorem for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.Google Scholar
[10]Ornstein, D. and Weiss, B.. The Shannon–McMillan–Breiman theorem for a class of amenable groups. Israel J. Math. 44 (1983), 53–60.CrossRefGoogle Scholar

