Article contents
Toeplitz flows and their ordered K-theory
Published online by Cambridge University Press: 11 February 2015
Abstract
To a Toeplitz flow 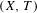 $(X,T)$ we associate an ordered
$(X,T)$ we associate an ordered 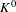 $K^{0}$ -group, denoted
$K^{0}$ -group, denoted 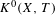 $K^{0}(X,T)$ , which is order isomorphic to the
$K^{0}(X,T)$ , which is order isomorphic to the 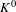 $K^{0}$ -group of the associated (non-commutative)
$K^{0}$ -group of the associated (non-commutative) 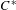 $C^{\ast }$ -crossed product
$C^{\ast }$ -crossed product 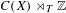 $C(X)\rtimes _{T}\mathbb{Z}$ . However,
$C(X)\rtimes _{T}\mathbb{Z}$ . However, 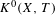 $K^{0}(X,T)$ can be defined in purely dynamical terms, and it turns out to be a complete invariant for (strong) orbit equivalence. We characterize the
$K^{0}(X,T)$ can be defined in purely dynamical terms, and it turns out to be a complete invariant for (strong) orbit equivalence. We characterize the 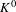 $K^{0}$ -groups that arise from Toeplitz flows
$K^{0}$ -groups that arise from Toeplitz flows 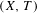 $(X,T)$ as exactly those simple dimension groups
$(X,T)$ as exactly those simple dimension groups 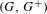 $(G,G^{+})$ that contain a non-cyclic subgroup
$(G,G^{+})$ that contain a non-cyclic subgroup 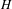 $H$ of rank one that intersects
$H$ of rank one that intersects  $G^{+}$ non-trivially. Furthermore, the Bratteli diagram realization of
$G^{+}$ non-trivially. Furthermore, the Bratteli diagram realization of 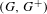 $(G,G^{+})$ can be chosen to have the ERS property, i.e. the incidence matrices of the Bratteli diagram have equal row sums. We also prove that for any Choquet simplex
$(G,G^{+})$ can be chosen to have the ERS property, i.e. the incidence matrices of the Bratteli diagram have equal row sums. We also prove that for any Choquet simplex 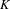 $K$ there exists an uncountable family of pairwise non-orbit equivalent Toeplitz flows
$K$ there exists an uncountable family of pairwise non-orbit equivalent Toeplitz flows 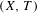 $(X,T)$ such that the set of
$(X,T)$ such that the set of  $T$ -invariant probability measures
$T$ -invariant probability measures 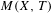 $M(X,T)$ is affinely homeomorphic to
$M(X,T)$ is affinely homeomorphic to 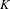 $K$ , where the entropy
$K$ , where the entropy 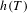 $h(T)$ may be prescribed beforehand. Furthermore, the analogous result is true if we substitute strong orbit equivalence for orbit equivalence, but in that case we can actually prescribe both the entropy and the maximal equicontinuous factor of
$h(T)$ may be prescribed beforehand. Furthermore, the analogous result is true if we substitute strong orbit equivalence for orbit equivalence, but in that case we can actually prescribe both the entropy and the maximal equicontinuous factor of 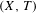 $(X,T)$ . Finally, we present some interesting concrete examples of dimension groups associated to Toeplitz flows.
$(X,T)$ . Finally, we present some interesting concrete examples of dimension groups associated to Toeplitz flows.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 3
- Cited by

