No CrossRef data available.
Article contents
Topologically mixing tiling of 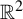 $\mathbb {R}^2$ generated by a generalized substitution
$\mathbb {R}^2$ generated by a generalized substitution
Published online by Cambridge University Press: 30 September 2021
Abstract
This paper presents sufficient conditions for a substitution tiling dynamical system of 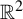 $\mathbb {R}^2$, generated by a generalized substitution on three letters, to be topologically mixing. These conditions are shown to hold on a large class of tiling substitutions originally presented by Kenyon in 1996. This problem was suggested by Boris Solomyak, and many of the techniques that are used in this paper are based on the work by Kenyon, Sadun, and Solomyak [Topological mixing for substitutions on two letters. Ergod. Th. & Dynam. Sys. 25(6) (2005), 1919–1934]. They studied one-dimensional tiling dynamical systems generated by substitutions on two letters and provided similar conditions sufficient to ensure that one-dimensional substitution tiling dynamical systems are topologically mixing. If a tiling dynamical system of
$\mathbb {R}^2$, generated by a generalized substitution on three letters, to be topologically mixing. These conditions are shown to hold on a large class of tiling substitutions originally presented by Kenyon in 1996. This problem was suggested by Boris Solomyak, and many of the techniques that are used in this paper are based on the work by Kenyon, Sadun, and Solomyak [Topological mixing for substitutions on two letters. Ergod. Th. & Dynam. Sys. 25(6) (2005), 1919–1934]. They studied one-dimensional tiling dynamical systems generated by substitutions on two letters and provided similar conditions sufficient to ensure that one-dimensional substitution tiling dynamical systems are topologically mixing. If a tiling dynamical system of 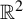 $\mathbb {R}^2$ satisfies our conditions (and thus is topologically mixing), we can construct additional topologically mixing tiling dynamical systems of
$\mathbb {R}^2$ satisfies our conditions (and thus is topologically mixing), we can construct additional topologically mixing tiling dynamical systems of  $\mathbb {R}^2$. By considering the stepped surface constructed from a tiling
$\mathbb {R}^2$. By considering the stepped surface constructed from a tiling 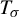 $T_\sigma $, we can get a new tiling of
$T_\sigma $, we can get a new tiling of 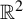 $\mathbb {R}^2$ by projecting the surface orthogonally onto an irrational plane through the origin.
$\mathbb {R}^2$ by projecting the surface orthogonally onto an irrational plane through the origin.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press


