Hostname: page-component-66644f4456-xp6jp Total loading time: 0 Render date: 2025-02-12T21:23:20.177Z Has data issue: true hasContentIssue false
  • English
  • Français

Traces on topological-graph algebras

Published online by Cambridge University Press:  02 May 2017

CHRISTOPHER SCHAFHAUSER
CHRISTOPHER SCHAFHAUSER*
Affiliation:
Pure Mathematics, University of Waterloo, 200 University Avenue West, Waterloo, ON, Canada, N2L 3G1 email cschafhauser@uwaterloo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a topological graph 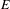$E$, we give a complete description of tracial states on the 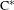$\text{C}^{\ast }$-algebra 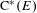$\text{C}^{\ast }(E)$ which are invariant under the gauge action; there is an affine homeomorphism between the space of gauge invariant tracial states on 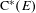$\text{C}^{\ast }(E)$ and Radon probability measures on the vertex space 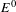$E^{0}$ which are, in a suitable sense, invariant under the action of the edge space 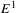$E^{1}$. It is shown that if $E$ has no cycles, then every tracial state on 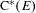$\text{C}^{\ast }(E)$ is gauge invariant. When 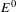$E^{0}$ is totally disconnected, the gauge invariant tracial states on 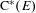$\text{C}^{\ast }(E)$ are in bijection with the states on 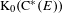$\text{K}_{0}(\text{C}^{\ast }(E))$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1923 - 1953
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afsar, Z., an Huef, A. and Raeburn, I.. KMS states on C∗ -algebras associated to local homeomorphisms. Internet. J. Math. 25 (2014), 1450066, 28pp.Google Scholar
Blackadar, B.. K-theory for Operator Algebras (Mathematical Sciences Research Institute Publications, 5) , 2nd edn. Cambridge University Press, Cambridge, 1998.Google Scholar
Blackadar, B. and Rørdam, M.. Extending states on preordered semigroups and the existence of quasitraces on C∗ -algebras. J. Algebra 152 (1992), 240–247.Google Scholar
Boyle, M. and Handelman, D.. Orbit equivalence, flow equivalence and ordered cohomology. Israel J. Math. 95 (1996), 169–210.CrossRefGoogle Scholar
Dixmier, J.. C∗ -algebras. North-Holland Publishing Company, Amersterdam, 1977.Google Scholar
Folland, G.. Real Analysis: Modern Techniques and Their Applications, 2nd edn. Wiley, New York, 1999.Google Scholar
Haagerup, U.. Quasitraces on exact C∗ -algebras are traces. C. R. Math. Acad. Sci. Soc. R. Can. 36 (2014), 67–92.Google Scholar
Hjelmborg, J. B.. Purely infinite and stable C∗ -alegbras of graphs and dynamical systems. Ergod. Th. & Dynam. Sys. 21 (2001), 1789–1808.Google Scholar
Johnson, M.. The graph traces of finite graphs and applications to tracial states of C∗ -algebras. New York J. Math. 11 (2005), 649–658.Google Scholar
Katsura, T.. A class of C∗ -algebras generalizing both graph algebra and homeomorphism C∗ -algebras I, fundamental results. Trans. Amer. Math. Soc. 356 (2004), 4287–4322.CrossRefGoogle Scholar
Katsura, T.. A class of C∗ -algebras generalizing both graph algebra and homeomorphism C∗ -algebras II, examples. Int. J. Math. 17 (2006), 791–833.Google Scholar
Katsura, T.. A class of C∗ -algebras generalizing both graph algebra and homeomorphism C∗ -algebras III, ideal structures. Ergod. Th. & Dynam. Sys. 26 (2006), 1805–1854.Google Scholar
Katsura, T.. A class of C∗ -algebras generalizing both graph algebra and homeomorphism C∗ -algebras IV, pure infinitenss. J. Funct. Anal. 254 (2008), 1161–1187.Google Scholar
Kirchberg, E.. On the existence of traces on exact stably projectionless simple C∗ -algebras. Operator Algebras and their Applications (Fields Institute Communications, 13) . Eds. Fillmore, P. A. and Mingo, J. A.. American Mathematical Society, Providence, RI, 1995, pp. 171–172.Google Scholar
Kumjian, A. and Li, H.. Twisted topological-graph algebras II, twisted groupoid $\text{C}^{\ast }$ -algebras. Preprint, 2015, arXiv:1507.04449 [math.OA].Google Scholar
Raeburn, I.. Graph Algebras (CBMS Regional Conference Series in Mathematics, 103) . American Mathematical Society, Providence, RI, 2005, published for the Conference Board of the Mathematical Sciences, Washington, DC.Google Scholar
Renault, J.. Cuntz-like algebras. Operator Theoretic Models (Timişoara, 1998). Theta Found, Bucharest, 2000, pp. 371–386.Google Scholar
Rørdam, M.. A simple C∗ -algebra with a finite and an infinite projection. Acta Math. 191 (2003), 109–142.Google Scholar
Tomforde, M.. The ordered K0 -group of a graph C∗ -algebras. C. R. Math. Acad. Sci. Soc. R. Can. 25 (2003), 19–25.Google Scholar
Webster, S. B. G.. The path space of a directed graph. Proc. Amer. Math. Soc. 142 (2014), 213–225.Google Scholar
Yeend, T.. Groupoid models for the C∗ -algebras of topological higher rank graphs. J. Operator Theory 57 (2007), 95–120.Google Scholar
Yeend, T.. Topoological higher-rank graphs and the C∗ -algebras of toplogical 1-graphs. Operator Theory, Operatator Algebras, and Applications (Contemporary Mathematics, 414) . American Mathematical Society, Providence, RI, 2006, pp. 231–244.Google Scholar