Article contents
Almost everywhere convergence of ergodic series
Published online by Cambridge University Press: 06 October 2015
Abstract
We consider ergodic series of the form 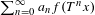 $\sum _{n=0}^{\infty }a_{n}f(T^{n}x)$ , where
$\sum _{n=0}^{\infty }a_{n}f(T^{n}x)$ , where 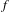 $f$ is an integrable function with zero mean value with respect to a
$f$ is an integrable function with zero mean value with respect to a  $T$ -invariant measure
$T$ -invariant measure  $\unicode[STIX]{x1D707}$ . Under certain conditions on the dynamical system
$\unicode[STIX]{x1D707}$ . Under certain conditions on the dynamical system  $T$ , the invariant measure
$T$ , the invariant measure  $\unicode[STIX]{x1D707}$ and the function
$\unicode[STIX]{x1D707}$ and the function  $f$ , we prove that the series converges
$f$ , we prove that the series converges  $\unicode[STIX]{x1D707}$ -almost everywhere if and only if
$\unicode[STIX]{x1D707}$ -almost everywhere if and only if 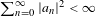 $\sum _{n=0}^{\infty }|a_{n}|^{2}<\infty$ , and that in this case the sum of the convergent series is exponentially integrable and satisfies a Khintchine-type inequality. We also prove that the system
$\sum _{n=0}^{\infty }|a_{n}|^{2}<\infty$ , and that in this case the sum of the convergent series is exponentially integrable and satisfies a Khintchine-type inequality. We also prove that the system 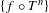 $\{f\circ T^{n}\}$ is a Riesz system if and only if the spectral measure of
$\{f\circ T^{n}\}$ is a Riesz system if and only if the spectral measure of 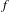 $f$ is absolutely continuous with respect to the Lebesgue measure and the Radon–Nikodym derivative is bounded from above as well as from below by a constant. We check the conditions for Gibbs measures
$f$ is absolutely continuous with respect to the Lebesgue measure and the Radon–Nikodym derivative is bounded from above as well as from below by a constant. We check the conditions for Gibbs measures  $\unicode[STIX]{x1D707}$ relative to hyperbolic dynamics
$\unicode[STIX]{x1D707}$ relative to hyperbolic dynamics  $T$ and for Hölder functions
$T$ and for Hölder functions 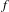 $f$ . An application is given to the study of differentiability of the Weierstrass-type functions
$f$ . An application is given to the study of differentiability of the Weierstrass-type functions 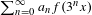 $\sum _{n=0}^{\infty }a_{n}f(3^{n}x)$ .
$\sum _{n=0}^{\infty }a_{n}f(3^{n}x)$ .
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 5
- Cited by

