Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MacKay, R. S.
1994.
Mode-locking and rotational chaos in networks of oscillators: A mathematical framework.
Journal of Nonlinear Science,
Vol. 4,
Issue. 1,
p.
301.
Kwapisz, Jaroslaw
1998.
Monotonicity of rotation set for toroidal chaos of a resonantly kicked linear oscillator.
Nonlinearity,
Vol. 11,
Issue. 3,
p.
547.
Guihéneuf, Pierre-Antoine
2015.
How roundoff errors help to compute the rotation set of torus homeomorphisms.
Topology and its Applications,
Vol. 193,
Issue. ,
p.
116.

 the rotation set ρ(
the rotation set ρ(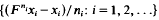 where
where 