Article contents
An inclination lemma for normally hyperbolic manifolds with an application to diffusion
Published online by Cambridge University Press: 10 July 2014
Abstract
Let (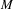 $M$,
$M$, 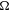 ${\rm\Omega}$) be a smooth symplectic manifold and
${\rm\Omega}$) be a smooth symplectic manifold and 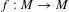 $f:M\rightarrow M$ be a symplectic diffeomorphism of class
$f:M\rightarrow M$ be a symplectic diffeomorphism of class 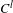 $C^{l}$ (
$C^{l}$ ( $l\geq 3$). Let
$l\geq 3$). Let 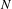 $N$ be a compact submanifold of
$N$ be a compact submanifold of 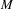 $M$ which is boundaryless and normally hyperbolic for
$M$ which is boundaryless and normally hyperbolic for  $f$. We suppose that
$f$. We suppose that 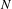 $N$ is controllable and that its stable and unstable bundles are trivial. We consider a
$N$ is controllable and that its stable and unstable bundles are trivial. We consider a 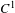 $C^{1}$-submanifold
$C^{1}$-submanifold 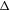 ${\rm\Delta}$ of
${\rm\Delta}$ of 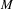 $M$ whose dimension is equal to the dimension of a fiber of the unstable bundle of
$M$ whose dimension is equal to the dimension of a fiber of the unstable bundle of 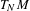 $T_{N}M$. We suppose that
$T_{N}M$. We suppose that 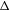 ${\rm\Delta}$ transversely intersects the stable manifold of
${\rm\Delta}$ transversely intersects the stable manifold of 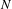 $N$. Then, we prove that for all
$N$. Then, we prove that for all  ${\it\varepsilon}>0$, and for
${\it\varepsilon}>0$, and for 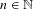 $n\in \mathbb{N}$ large enough, there exists
$n\in \mathbb{N}$ large enough, there exists 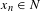 $x_{n}\in N$ such that
$x_{n}\in N$ such that 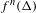 $f^{n}({\rm\Delta})$ is
$f^{n}({\rm\Delta})$ is  ${\it\varepsilon}$-close, in the
${\it\varepsilon}$-close, in the 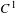 $C^{1}$ topology, to the strongly unstable manifold of
$C^{1}$ topology, to the strongly unstable manifold of 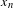 $x_{n}$. As an application of this
$x_{n}$. As an application of this  ${\it\lambda}$-lemma, we prove the existence of shadowing orbits for a finite family of invariant minimal sets (for which we do not assume any regularity) contained in a normally hyperbolic manifold and having heteroclinic connections. As a particular case, we recover classical results on the existence of diffusion orbits (Arnold’s example).
${\it\lambda}$-lemma, we prove the existence of shadowing orbits for a finite family of invariant minimal sets (for which we do not assume any regularity) contained in a normally hyperbolic manifold and having heteroclinic connections. As a particular case, we recover classical results on the existence of diffusion orbits (Arnold’s example).
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 7
- Cited by

