Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fried, David
1982.
Subshifts on surfaces.
Ergodic Theory and Dynamical Systems,
Vol. 2,
Issue. 1,
p.
15.
Batterson, Steve
and
Smillie, John
1985.
Smale diffeomorphisms and surface topology.
Ergodic Theory and Dynamical Systems,
Vol. 5,
Issue. 4,
p.
519.
Béguin, F.
Bonatti, C.
and
Vieitez, J. L.
1999.
Construction de flots de Smale en dimension 3.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 8,
Issue. 3,
p.
369.
A. De Rezende, Ketty
and
G. Villapouca, Mariana
2017.
Discrete conley index theory for zero dimensional basic sets.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 3,
p.
1359.

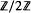 ). Since there are infinitely many subshifts of finite type whose reduced zeta functions do not satisfy these restrictions, there are infinitely many subshifts which cannot be basic sets for any diffeomorphism of any surface.
). Since there are infinitely many subshifts of finite type whose reduced zeta functions do not satisfy these restrictions, there are infinitely many subshifts which cannot be basic sets for any diffeomorphism of any surface.