Anosov flows on $3$-manifolds: the surgeries and the foliations

Abstract

Every Anosov flow on a 3-manifold is associated to a bifoliated plane (a plane endowed with two transverse foliations 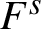$F^s$ and 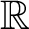$F^u$ ) which reflects the normal structure of the flow endowed with the center-stable and center-unstable foliations. A flow is 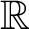$\mathbb{R}$ -covered if 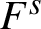$F^s$ (or equivalently 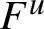$F^u$ ) is trivial. On the other hand, from any Anosov flow one can build infinitely many others by Dehn–Goodman–Fried surgeries. This paper investigates how these surgeries modify the bifoliated plane. We first observe that surgeries along orbits corresponding to disjoint simple closed geodesics do not affect the bifoliated plane of the geodesic flow of a hyperbolic surface (Theorem 1). Analogously, for any non- 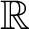$\mathbb{R}$ -covered Anosov flow, surgeries along pivot periodic orbits do not affect the branching structure of its bifoliated plane (Theorem 2). 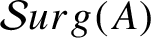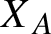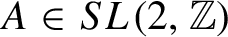Next, we consider the set $\mathcal{S}urg(A)$ of Anosov flows obtained by Dehn–Goodman–Fried surgeries from the suspension flow $X_A$ of any hyperbolic matrix $A \in SL(2,\mathbb{Z})$ . Fenley proved that performing only positive (or negative) surgeries on 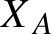$X_A$ leads to 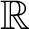$\mathbb{R}$ -covered Anosov flows. We study here Anosov flows obtained by a combination of positive and negative surgeries on 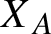$X_A$ . Among other results, we build non- 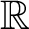$\mathbb{R}$ -covered Anosov flows on hyperbolic manifolds. 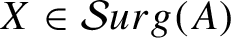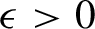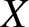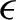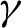Furthermore, we show that given any flow $X\in \mathcal{S}urg(A)$ there exists $\epsilon>0$ such that every flow obtained from $X$ by a non-trivial surgery along any $\epsilon$ -dense periodic orbit $\gamma$ is 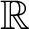$\mathbb{R}$ -covered (Theorem 4). 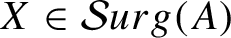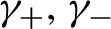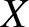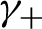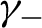Analogously, for any flow $X \in \mathcal{S}urg(A)$ there exist periodic orbits $\gamma_+,\gamma_-$ such that every flow obtained from $X$ by surgeries with distinct signs on $\gamma_+$ and $\gamma_-$ is non- 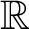$\mathbb{R}$ -covered (Theorem 5).

1 Introduction

1.1 General setting

In this paper we consider Anosov flows on closed $3$ -manifolds, up to topological (orbital) equivalence.

Following the pioneering work of Handel and Thurston [HT] on geodesic flows, Goodman [Go] proved that for any Anosov flow X on a manifold M and any periodic orbit $\gamma $ , one can build a new Anosov flow on a manifold obtained from M by a Dehn surgery along $\gamma $ . In Goodman’s construction, the dynamics of the new Anosov flow was not easy to understand. In [Fri], Fried proposed an alternative to the Dehn–Goodman surgery, for which the dynamics of the flow obtained from X is topologically equivalent to X except on $\gamma $ . It was implicit in Fried’s paper that his (topological) Anosov flow was indeed orbitally equivalent to that obtained by Dehn–Goodman surgery and the mathematics community generally admitted this during the 1980s and 1990s (see, for instance, [Fe1]), before noticing that there was no explicit proof of such a statement. The orbital equivalence between Goodman’s and Fried’s surgery was indeed an open question. It was only recently that this was proven by Shannon, who proves in his thesis that Fried’s surgery is indeed orbitally equivalent to Dehn–Goodman surgery and that any topological Anosov flow is orbitally equivalent to an Anosov flow (see also [Sh]). A first attempt to prove that a topological Anosov flow obtained by Fried’s surgery is orbitally equivalent to a smooth Anosov flow was made by Brunella in his thesis [Bru]. However, Brunella’s proof relied on the erroneous fact that isotopic pseudo-Anosov diffeomorphisms on surfaces with boundary are all conjugated.

Assume that M is orientable and that $\gamma $ is a periodic orbit with positive eigenvalues. Then the boundary of a tubular neighbourhood of $\gamma $ is a torus endowed with a canonical meridian, parallel basis of its fundamental group. In this basis, the Dehn–Goodman–Fried surgery involves keeping the same parallel and adding n parallels to the meridian, we therefore speak of a surgery of characteristic number n. We also define a positive or negative surgery along $\gamma $ according to the sign of the characteristic number n.

One of the main open questions of this field (stated by Fried in [Fri]) is as follows.

Question 1.1. Is any transitive Anosov flow obtained through a finite sequence of Dehn–Goodman–Fried surgeries from the suspension flow of a hyperbolic linear automorphism of the torus ${\mathbb T}^{2}$ ?

The aim of this paper is to study the Anosov flows obtained by a finite sequence of surgeries from a suspension Anosov flow, that is, conjecturally, all the Anosov flows on $3$ -manifolds.

1.2 ${\mathbb R}$ -covered and non- ${\mathbb R}$ -covered Anosov flows

Our point of view here is to consider the effect of surgeries on the bifoliated plane associated to an Anosov flow X, in order to decide whether the flow is ${\mathbb R}$ -covered or not. Let us recall these notions.

In [Ba1, Fe1], Barbot and Fenley show simultaneously that for any Anosov flow X on a $3$ -manifold M, its lift $\tilde {X}$ on the universal cover $\tilde M$ is conjugated to the constant vector field $\partial /{\partial x}$ on ${\mathbb R}^{3}$ . The space of orbits of $\tilde X$ is therefore a $2$ -plane ${\mathcal P}_{X}\simeq {\mathbb R}^{2}$ , endowed with the natural quotient of the lift of the weak stable and unstable manifolds of X on $\tilde M$ . In other words, any Anosov flow X is naturally associated to a pair of transverse foliations $F^{s}_{X}, F^{u}_{X}$ on the plane ${\mathcal P}_{X}$ : we call $({\mathcal P}_{X},F^{s}_{X},F^{u}_{X})$ the bifoliated plane associated to X.

In both [Ba1, Fe1] it has been proven that if the space of leaves of $F^{s}_{X}$ is Hausdorff, then the same happens to the space of leaves of $F^{u}_{X}$ . In this case, we say that X is ${\mathbb R}$ -covered (Figure 1). When the previous hypotheses are not satisfied, we say that X is non- ${\mathbb R}$ -covered (see Figure 2).

Figure 1 $\mathbb {R}$ -covered flows. Colour available online.

Figure 2 Non- $\mathbb {R}$ -covered flow. Colour available online.

If X is ${\mathbb R}$ -covered, [Fe1] shows that the bifoliated plane $({\mathcal P}_{X},F^{s}_{X},F^{u}_{X}$ ) is conjugated to one of the following two models:

• • ${\mathbb R}^{2}$ endowed with the two foliations by parallel horizontal and vertical straight lines. We say in this case that ${\mathbb R}^{2}$ is trivially bifoliated (see Figure 1(a)). According to a Theorem of Solodov, this case corresponds to suspension flows (see [Ba]).

• • the restrictions of the trivial horizontal/vertical foliations of ${\mathbb R}^{2}$ to the strip $\{(x,y)\in {\mathbb R}^{2}, |x-y|<1 \}$ . We say in this case that X is twisted ${\mathbb R}$ -covered (see Figure 1(b),(c)).

[Fe1] shows that if X is an Anosov flow on a non-orientable manifold M, then it cannot be twisted ${\mathbb R}$ -covered: it is either trivially bifoliated or non- ${\mathbb R}$ -covered. For this reason, from now on, the manifold M will be assumed to be oriented. In this case, the bifoliated plane is naturally oriented. If X is twisted ${\mathbb R}$ -covered, the bifoliated plane $({\mathcal P}_{X},F^{s}_{X},F^{u}_{X}$ ) is conjugated to one of the two models by an orientation-preserving homeomorphism:

• • the restrictions of the trivial horizontal/vertical foliations of ${\mathbb R}^{2}$ to the strip $\{(x,y)\in {\mathbb R}^{2}, |x-y|<1 \}$ . In this case, we say that X is ${\mathbb R}$ -covered positively twisted (see Figure 1(b)).

• • the restrictions of the trivial horizontal/vertical foliations of ${\mathbb R}^{2}$ to the strip $\{(x,y)\in {\mathbb R}^{2}, |x+y|<1 \}$ . In this case, we say that X is ${\mathbb R}$ -covered negatively twisted (see Figure 1(c)).

For instance, the geodesic flow of a hyperbolic closed surface (or orbifold) is twisted ${\mathbb R}$ -covered. Here is an example which is typical of the results we obtain.

Theorem 1. Let S be a hyperbolic closed surface and X the geodesic flow on $M= T^{1}(S)$ . By choosing the orientation of M, we can assume X to be ${\mathbb R}$ -covered positively twisted.

Let $a_{1},\ldots ,a_{k}$ be a set of simple closed disjoint geodesics and $\Gamma =\{\pm \gamma _{i}\}$ be the set of corresponding orbits of X.

Then any flow Y obtained from X by surgeries along $\Gamma $ is ${\mathbb R}$ -covered positively twisted.

In other words, surgeries along non-intersecting closed geodesics have no effect on the bifoliated plane up to homeomorphism.

Non- ${\mathbb R}$ -covered flows also admit a specific set of orbits for which the corresponding surgeries have a very limited effect on the bifoliated plane. More precisely, [Fe2] defined the notion of pivot points in the bifoliated plane ${\mathcal P}_{X}$ of a non- ${\mathbb R}$ -covered Anosov flow (see Figure 3 and §6 for a precise definition) and he proved that they correspond to a finite set ${{\mathcal P}}iv(X)$ of periodic orbits.

Figure 3 A pivot point.

We prove the following result (see Theorem 14 for a more precise and stronger statement).

Theorem 2. Let X be a non- ${\mathbb R}$ -covered Anosov flow and let Y be obtained from X by a finite number of Dehn surgeries along orbits of ${{\mathcal P}}iv(X)$ . Then (up to the natural identification of the orbits of Y with the orbits of X) one has ${{\mathcal P}}iv(Y)={{\mathcal P}}iv(X)$ .

It is still unknown whether surgeries along pivot points lead to bifoliated planes that are the same up to homeomorphism. We only have a limited set of examples where this is the case.

In [Fe2], Fenley proved that a non- ${\mathbb R}$ -covered Anosov flow has non-separated leaves in both $F^{s}_{X}$ and $F^{u}_{X}$ and that they correspond to finitely many periodic orbits, which we denote by ${\mathcal S}(X):= {\mathcal S}^{s}(X) \cup {\mathcal S}^{u}(X)$ . Surgeries along orbits in ${\mathcal S}(X)$ have also a limited effect on the bifoliated plane.

Theorem 3. Let X be a non- ${\mathbb R}$ -covered Anosov flow with oriented stable/unstable bundles and let Y be obtained from X by any Dehn surgery along a periodic orbit in ${\mathcal S}(X)$ . Then Y is not ${\mathbb R}$ -covered.

In Theorem 15 we explain in a more detailed way which aspects of the bifoliated plane are preserved by surgeries along orbits in ${\mathcal S}(X)$ .

Our main results concern Anosov flows (up to orbital equivalence) obtained by surgeries from a suspension.

In this paper, $A\in SL(2,{\mathbb Z})$ denotes a hyperbolic matrix (not necessarily of positive trace) and $f_{A}\colon {\mathbb T}^{2}\to {\mathbb T}^{2}$ the induced linear automorphism. We denote by $M_{A},X_{A}$ the mapping torus manifold $M_{A}$ endowed with the suspension flow $X_{A}$ . We will consider the set ${{\mathcal S}}urg(A)$ of Anosov flows (up to orbital equivalence) obtained from $(M_{A}, X_{A})$ through a finite sequence of Dehn–Goodman–Fried surgeries. A recent result, announced by Minakawa [Mi] and recently written up by Dehornoy and Shannon [DeSh], shows that if $A,B\in SL(2,{\mathbb Z})$ are two hyperbolic matrices with positive eigenvalues then

$$ \begin{align*} {{\mathcal S}}urg(A)={{\mathcal S}}urg(B). \end{align*} $$

We will denote this set by ${{\mathcal S}}urg_{+}$ (the $+$ index refers to the positive eigenvalues of the matrices that we consider). It is known that ${{\mathcal S}}urg_{+}$ contains the geodesic flows of hyperbolic surfaces and orbifolds (see [DeSh, Fri]).

The aim of this paper is to describe the bifoliated plane $({\mathcal P}_{X}, F^{s}_{X},F^{u}_{X})$ for $X\in {{\mathcal S}}urg(A)$ , as a function of the surgeries (periodic orbits and characteristic numbers) performed on $X_{A}$ in order to obtain X.

1.3 The case of two periodic orbits

In [Fe1], Fenley shows that if Y is an Anosov flow obtained from $X_{A}$ by performing finitely many Dehn surgeries, all positive, then Y is positively twisted ${\mathbb R}$ -covered. This obviously covers the case of a surgery along a unique periodic orbit of $X_{A}$ .

Let us now consider the set of flows ${{\mathcal S}}urg(A,\gamma _{+},\gamma _{-})$ obtained from $X_{A}$ after performing surgeries along two periodic orbits $\gamma _{+}$ and $\gamma _{-}$ . There is a natural parametrization of ${{\mathcal S}}urg(A,\gamma _{+},\gamma _{-})$ by the characteristic numbers of the surgeries along $\gamma _{+}$ and $\gamma _{-}$ , therefore a parametrization by ${\mathbb Z}^{2}$ . Section 9 is devoted to the study of vector fields in ${{\mathcal S}}urg(A,\gamma _{+},\gamma _{-})$ which will be denoted by $Z_{m,n}$ , $m,n\in {\mathbb Z}$ , where m and n are the characteristic numbers of the surgeries performed along $\gamma _{+}$ and $\gamma _{-}$ , respectively.

In this simple case, our goal is to describe, in terms of $\gamma _{+}$ and $\gamma _{-}$ , the regions of ${\mathbb Z}^{2}$ where we can decide whether $Z_{m,n}$ is ${\mathbb R}$ -covered or not, and twisted (positively or negatively) or not.

Related to this problem is a question by Mario Shannon (which we do not answer here).

Question 1.2. (Shannon)

Do there exist $A,\gamma _{+},\gamma _{-}$ , $\gamma _{+}\neq \gamma _{-}$ and $(m,n)\in {\mathbb Z}^{2}\setminus \{(0,0)\}$ such that $Z_{m,n}$ is a suspension flow?

Proposition 9.1 shows that, given $A,\gamma _{+},\gamma _{-}$ , there are at most finitely many $(m,n)$ for which the answer to the question can be positive. More generally, we think it is possible to prove that, given a matrix A, there are at most finitely many $4$ -tuples $(\gamma _{+},m,\gamma _{-},n)$ for which the answer is positive.

According to [Fe1], we know that if $m\geq 0$ and $n\geq 0$ (respectively, $m\leq 0$ and $n\leq 0$ ) and $(m,n)\neq (0,0)$ then the flow $Z_{m,n}$ is ${\mathbb R}$ -covered and positively (respectively, negatively) twisted. When m and n have opposite signs, one could expect a competition between the effects of the surgeries along $\gamma _{+}$ and $\gamma _{-}$ on the bifoliated plane, as they twist this plane in opposite directions: either one is dominating the other, leading to an ${\mathbb R}$ -covered twisted flow, or the bifoliated plane is positively twisted in some places and negatively in other places (whatever that means), leading to a non- ${\mathbb R}$ -covered flow. We will see that the result of this competition depends on the mutual positions of the orbits $\gamma _{+},\gamma _{-}$ . This remark will be made more precise in §2 and a complete overview of the case of two periodic orbits will be given in §9. Let us now move on to the general setting.

1.4 Two typical effects of surgeries on the bifoliated plane

According to [Fe1], performing finitely many positive Dehn surgeries on $X_{A}$ twists the bifoliated plane positively.

Here we consider the effect of positive and negative surgeries on the bifoliated plane.

Theorem 4. Let $A\in SL(2,{\mathbb Z})$ be a hyperbolic matrix and $X\in {{\mathcal S}}urg(A)$ . Then there is $\varepsilon>0$ such that for any periodic orbit $\gamma $ which is $\varepsilon $ -dense all the flows Y obtained from X by surgeries along $\gamma $ are ${\mathbb R}$ -covered twisted positively or negatively according to the sign of the surgery on $\gamma $ .

Conjecturally every transitive Anosov flow with transversally oriented foliations on an oriented $3$ -manifold belongs to ${{\mathcal S}}urg_{+}$ . It is therefore natural to ask if it is possible to prove the following conjecture.

Conjecture 1. Let X be a transitive Anosov flow on an oriented $3$ -manifold. Then there is $\varepsilon>0$ such that for any periodic orbit $\gamma $ which is $\varepsilon $ -dense all the flows Y obtained from X by surgeries along $\gamma $ are ${\mathbb R}$ -covered twisted positively or negatively according to the sign of the surgery on $\gamma $ .

Recently, there has been a lot of progress towards a proof of this conjecture (see [As, Mar]). A complete and positive answer has been announced by the first author of this paper in [Bo].

If the answer to Question 1.1 is affirmative, then the Conjecture 1 is a straightforward consequence of Theorem 4. One can also think of Conjecture 1 as an intermediary step for answering Question 1.1.

Contrary to Theorem 4, which describes a process of construction of ${\mathbb R}$ -covered flows, our next result goes in the opposite direction, leading to the construction of non- ${\mathbb R}$ -covered Anosov flows.

Theorem 5. Let $A\in SL(2,{\mathbb Z})$ be a hyperbolic matrix and $X\in {{\mathcal S}}urg(A)$ . Then there exist periodic orbits $\gamma _{+}$ and $\gamma _{-}$ such that all the flows Y obtained from X by surgeries of distinct signs along $\gamma _{+}$ and $\gamma _{-}$ are not ${\mathbb R}$ -covered.

In Theorems 4 and 5 we start with any flow obtained from a suspension flow by finitely many surgeries and we exhibit orbits along which surgeries lead to ${\mathbb R}$ -covered or non- ${\mathbb R}$ -covered flows. In other words, the effect of the initial surgeries can be neglected when compared with the effect of the new surgeries. We will see in Theorems 6 and 7 more general versions of the previous results: given a finite set ${\mathcal E}$ of periodic orbits, we prove the existence of one orbit $\gamma $ or two orbits $\gamma _{+}$ and $\gamma _{-}$ such that no matter what surgeries one may perform along the orbits in ${\mathcal E}$ , the result ( ${\mathbb R}$ -covered or non- ${\mathbb R}$ -covered) only depends on the (non-trivial) surgeries performed along $\gamma $ or $\gamma _{+}\cup \gamma _{-}$ , respectively.

Theorems 4 and 5 (and indeed Theorems 6 and 7) are existence results: they ensure the existence of a periodic orbit $\gamma $ or two orbits $\gamma _{+}$ and $\gamma _{-}$ with prescribed effects on the bifoliated plane. However, they do not provide any criterion for deciding whether an orbit $\gamma $ or two orbits $\gamma _{+}$ and $\gamma _{-}$ satisfy their conclusions. Theorems 8 and 9 provide a sufficient and explicit geometric condition for surgeries along a set of periodic orbits to lead to ${\mathbb R}$ -covered or non- ${\mathbb R}$ -covered Anosov flows. The previous criterion is satisfied in a great variety of cases. Explicit examples of bifoliated planes and orbits satisfying this condition are examined in §§9 and 10.

The precise statement of these stronger results is postponed until §2.

1.5 Structure of the paper

In §2 we begin by presenting some more technical, but much stronger, versions of Theorems 4 and 5, namely Theorems 6–9.

In §3 we recall basic definitions and properties of Anosov flows on $3$ -manifolds. In particular, we recall the works of Fenley and Barbot on the bifoliated plane, a characterization of ${\mathbb R}$ -covered and non- ${\mathbb R}$ -covered Anosov flows and finally some properties of the Dehn–Goodman–Fried surgery.

In §4 we recall very basic facts allowing us to compare the bifoliated planes associated to two Anosov flows X and Y obtained one from the other by surgeries. This leads to a general procedure defined in Theorem 13 for comparing the holonomies of the foliations of both bifoliated planes. When X is a suspension flow, the procedure in Theorem 13 can be made more explicit and will be called the dynamical game for computing the holonomies.

In §5 we give a general criterion (see Corollary 5.1) ensuring that surgeries along a finite set of periodic orbits cannot break the ${\mathbb R}$ -covered property. Then we apply Corollary 5.1 to the geodesic flow of hyperbolic surfaces and prove Theorem 1.

In §6 we prove Theorems 14 and 15, which are more precise and stronger versions of Theorems 2 and 3 concerning surgeries which do not change the branching structure of non- ${\mathbb R}$ -covered Anosov flows. This essentially involves recalling the description of this branching structure given in [Fe2] and in applying the general tools of §4.

More particularly, §7 ends with the proof of Theorems 4 and 7 in which we prove that for $X\in {\mathcal S} urg_{+}$ any surgery on an $\varepsilon $ -dense periodic orbit, for $\varepsilon>0$ small enough, provides an ${\mathbb R}$ -covered flow. In order to prove the previous statement, we begin by proving Theorem 8, and we proceed by carefully replacing the strong enough surgeries hypothesis in Theorem 8 by the $\varepsilon $ -density hypothesis.

Section 8, being the non-separated counterpart of §7, follows the same structure. We begin by proving Theorem 9 and we proceed by replacing the strong enough surgeries condition by an $\varepsilon $ -density condition, thus proving Theorems 5 and 6.

In §9 we consider the flows $X\in {\mathcal S} urg_{+}$ obtained from a suspension by surgeries along two periodic orbits. In this case, by applying Theorems 8 or 9 we get a complete overview of the flows X obtained from $X_{A}$ by strong enough surgeries.

Having mostly considered surgeries along orbits of very large periods (the period of an $\varepsilon $ -dense orbit tends to infinity as $\varepsilon $ goes to $0$ ) in §§7 and 8, in order to present explicit examples of orbits of small periods ( $1$ or $3$ ), we focus in §10 on the matrices

$$ \begin{align*}A_{n}=\left(\begin{array}{@{}cc@{}} n&n-1\\ 1&1 \end{array}\right)\end{align*} $$

and their cubes $B_{n}=A_{n}^{3}$ . We will apply the criteria of §§7 and 8 to the orbits of the points $(0,0)$ and $(\tfrac 12,\tfrac 12)$ .

2 Some stronger versions of Theorems 4 and 5

2.1 Existence of dominating surgeries

In Theorems 4 and 5 we start with any flow obtained from a suspension flow by finitely many surgeries and we exhibit orbits on which surgeries lead to ${\mathbb R}$ -covered or non- ${\mathbb R}$ -covered flows.

As promised at the end of the introduction, in this section we will state Theorems 6 and 7 which are more general versions of Theorems 4 and 5: given a finite set ${\mathcal E}$ of periodic orbits, there is one orbit $\gamma $ or two orbits $\gamma _{+}$ and $\gamma _{-}$ on which the surgeries dominate any surgery along the orbits in ${\mathcal E}$ . We furthermore notice in the addenda to Theorems 6 and 7 that most of these surgeries lead to hyperbolic $3$ -manifolds.

Theorem 6. Let $A\in SL(2,{\mathbb Z})$ a hyperbolic matrix and ${\mathcal E}$ be a finite A-invariant set. Then there exist periodic orbits $\gamma _{+}$ and $\gamma _{-}$ such that every flow Y obtained from $X_{A}$ by any surgery on ${\mathcal E}$ and any two surgeries of distinct signs along $\gamma _{+}$ and $\gamma _{-}$ is not ${\mathbb R}$ -covered.

Addendum to Theorem 6. Let ${\mathcal E}$ be the union of the periodic orbits $p_{1},\ldots ,p_{n}$ . There exists $N \in \mathbb {N}$ such that if the absolute values of all the indices of the surgeries along $\gamma _{+},\gamma _{-},p_{1},\ldots ,p_{n}$ are greater than N and the surgeries along $\gamma _{+}$ and $\gamma _{-}$ are of distinct signs, then the resulting flow Y is non- ${\mathbb R}$ -covered and is supported by a hyperbolic manifold.

Interestingly enough, Theorem 6 implies that the surgeries along ${\mathcal E}$ seem negligible in comparison with the ones on $\gamma _{+}$ and $\gamma _{-}$ . This is also the case for Theorem 4, which also admits the following stronger version.

Theorem 7. Let ${\mathcal E}\subset {\mathbb T}^{2}$ be a finite $f_{A}$ -invariant set. There is $\varepsilon>0$ such that for any finite, $\varepsilon $ -dense and $f_{A}$ -invariant set ${\mathcal Y}\subset {\mathbb T}^{2}$ one has the following property. Let Y be any flow obtained from $X_{A}$ by surgeries along ${\mathcal E}\cup {\mathcal Y}$ and such that the characteristic numbers of the surgeries on ${\mathcal Y}$ are non-zero and have the same signs $\omega _{{\mathcal Y}}\in \{+,-\}$ . Then Y is ${\mathbb R}$ -covered and twisted, positively or negatively according to $\omega _{{\mathcal Y}}$ .

Addendum to Theorem 7. Furthermore, let ${\mathcal Y}$ (respectively, ${\mathcal E}$ ) be the union of the periodic orbits $d_{1},\ldots ,d_{n}$ (respectively, $p_{1},\ldots ,p_{m}$ ). There exists $N \in \mathbb {N}$ such that if the absolute values of all the indices of the surgeries along $d_{1},\ldots ,d_{n},p_{1},\ldots ,p_{m}$ are greater than N and the surgeries on ${\mathcal Y}$ are either all positive or all negative, then the resulting flow Y is ${\mathbb R}$ -covered and is supported by a hyperbolic manifold.

Thus Theorems 6 and 7 consider well-chosen sets of periodic orbits ${\mathcal Y}$ , on which surgeries dominate all surgeries on a given set ${\mathcal E}$ . We are still very far from understanding the general case.

Problem 1. Consider a vector field Y obtained from $X_{A}$ by performing positive surgeries on a finite A-invariant set $\Gamma _{+}$ with strength $n_{+}\colon \Gamma _{+}\to {\mathbb N}^{*}$ , and negative surgeries on a finite A-invariant set $\Gamma _{-}$ with strength $n_{-}\colon \Gamma _{-}\to -{\mathbb N}^{*}$ . Knowing $(\Gamma _{+},n_{+}),(\Gamma _{-},n_{-})$ , can we decide whether Y is ${\mathbb R}$ -covered or not?

In the next section we describe several settings where we can answer the previous question.

2.2 A geometric criterion on periodic orbits for surgery domination

As stated above, given an invariant finite set ${\mathcal E}$ , Theorems 6 and 7 assert the existence of periodic orbits ( $\gamma $ or $\gamma _{+}$ and $\gamma _{-}$ ) for which the surgeries dominate any surgery along ${\mathcal E}$ . We will see in this section that this phenomenon is due to the geometric properties of the relative position with respect to ${\mathcal E}$ of the announced periodic orbits ( $\gamma $ or $\gamma _{+}$ and $\gamma _{-}$ ). The aim of this section is to state Theorems 8 and 9 which provide criteria for surgery domination by using rectangles in the bifoliated plane.

Let us fix a hyperbolic matrix $A\in SL(2,{\mathbb Z})$ (not necessarily of positive trace), $X_{A}$ its associated suspension Anosov flow and two disjoint finite $f_{A}$ -invariant sets ${\mathcal X},{\mathcal Y}$ . Consider ${\mathcal X}$ (respectively, ${\mathcal Y}$ ) to be the union of the periodic orbits $ \lbrace x_{i}\rbrace _{i\in I}$ (respectively, $\lbrace y_{j}\rbrace _{j\in J}$ ). We denote by ${{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y})$ the set of Anosov flows obtained by performing surgeries along ${\mathcal X} \cup {\mathcal Y}$ , and by ${{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},(m_{i})_{i\in I},\ast )$ the set of Anosov flows obtained by performing any kind of surgery along ${\mathcal Y}$ and surgeries with characteristic numbers $m_{i}$ along $x_{i}$ . We give an analogous meaning to the notation ${{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ . Similarly, ${{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},(m_{i})_{i\in I}, (n_{j})_{j\in J})$ denotes the flow obtained by the surgeries with characteristic numbers $(m_{i})$ and $(n_{j})$ .

We consider the plane ${\mathbb R}^{2}$ (seen as the bifoliated plane associated to $X_{A}$ ) endowed with the lattice ${\mathbb Z}^{2}$ and the eigendirections $E^{s}_{A}, E^{u}_{A}$ . We fix an orientation for $E^{s}_{A}$ and $E^{u}_{A}$ . We denote by $F^{s}_{A}$ and $F^{u}_{A}$ the (trivial) foliations of ${\mathbb R}^{2}$ by affine lines parallel to the eigendirections. For any finite $f_{A}$ -invariant set ${\mathcal E}$ , we denote by $\tilde {{\mathcal E}}$ its lift on ${\mathbb R}^{2}$ . A rectangle is a topological disc $R\subset {\mathbb R}^{2}$ whose boundary consists of the union of two segments of leaves of $F^{s}_{A}$ and two segments of leaves of $F^{u}_{A}$ .

A rectangle R has two diagonals. The orientations of $E^{s}_{A}$ and $E^{u}_{A}$ allow us to speak of the increasing and the decreasing diagonal. We endow the diagonals with the transverse orientation of $E^{s}_{A}$ , so that each diagonal has a first point (or else origin) and a last point.

If ${\mathcal E}\subset {\mathbb T}^{2}$ is a finite $f_{A}$ -invariant subset of the torus ${\mathbb T}^{2}= {\mathbb R}^{2}/{\mathbb Z}^{2}$ , we say that a rectangle R is a positive (respectively, negative) ${\mathcal E}$ -rectangle if the endpoints of its increasing (respectively, decreasing) diagonal belong to the lift $\tilde {\mathcal E}$ on ${\mathbb R}^{2}$ of ${\mathcal E}$ .

A positive or negative ${\mathcal E}$ -rectangle R is primitive if $R\cap \tilde {\mathcal E}$ consists of the endpoints of its increasing or decreasing diagonal.

We are ready to state our first geometric criterion, which is a geometric version of Theorem 4.

Theorem 8. Let $A\in SL(2,{\mathbb Z})$ be a hyperbolic matrix and ${\mathcal X},{\mathcal Y}$ two disjoint finite $f_{A}$ -invariant sets. Assume that every positive ${\mathcal X}$ -rectangle contains a point of $\tilde {{\mathcal Y}}$ . Then there is $N>0$ such that every Anosov flow in ${{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ with $n_{j}\geq N$ is ${\mathbb R}$ -covered and positively twisted.

Obviously, the same statement holds:

• • by exchanging ${\mathcal X}$ with ${\mathcal Y}$ ;

• • by replacing ‘positive rectangle’ and ‘positively twisted’ by ‘negative rectangle’ and ‘negatively twisted’.

As we will see in the next observations, the geometric hypotheses in Theorem 8 for any ${\mathcal X}$ -rectangle are indeed conditions on a finite number of rectangles.

Indeed, for any finite $f_{A}$ -invariant set ${\mathcal E}$ , since A is orientation-preserving and the foliations $F^{s}_{A},F^{u}_{A}$ are invariant, one can make the following observation.

Remark 2.1. If R is a rectangle, then $A(R)$ is a rectangle. If R is a positive ${\mathcal E}$ -rectangle, then $A(R)$ is a positive ${\mathcal E}$ -rectangle. If R is primitive, then $A(R)$ is primitive.

In the same way, the notion of primitive (respectively, positive, negative) ${\mathcal E}$ -rectangle is invariant under translations by elements of ${\mathbb Z}^{2}$ .

Lemma 2.1. For any finite $f_{A}$ -invariant set ${\mathcal E} \subset {\mathbb T}^{2}$ , there are finitely many orbits of primitive ${\mathcal E}$ -rectangles, for the action of the group generated by A and the integer translations.

Therefore, the hypothesis in Theorem 8, namely the fact that every positive ${\mathcal X}$ -rectangle contains a point of $\tilde {{\mathcal Y}}$ , can be checked on a finite number of positive primitive ${\mathcal X}$ -rectangles.

Using Lemma 2.1, we get that many pairs $({\mathcal X},{\mathcal Y})$ satisfying the hypotheses of Theorem 8.

Lemma 2.2. Given any $f_{A}$ -invariant finite set ${\mathcal X}$ , there is $\varepsilon>0$ such that every $\varepsilon $ -dense finite invariant set ${\mathcal Y}$ intersects every ${\mathcal X}$ -rectangle. Such a pair $({\mathcal X},{\mathcal Y})$ satisfies the hypotheses of Theorem 8.

Theorem 8 states that if every positive ${\mathcal X}$ -rectangle contains a point of $\tilde {{\mathcal Y}}$ , then the surgeries on ${\mathcal Y}$ dominate the surgeries on ${\mathcal X}$ . It turns out that under the previous condition, it is not possible for the surgeries on ${\mathcal X}$ to also dominate the surgeries on ${\mathcal Y}$ . We thus get the following corollary to Theorem 8.

Lemma 2.3. If $\tilde {{\mathcal Y}}$ intersects every positive ${\mathcal X}$ -rectangle, then there is a negative ${\mathcal Y}$ -rectangle disjoint from $\tilde {{\mathcal X}}$ .

The following result can be seen as a geometric version of Theorem 5. It states our second geometric criterion which is based on the existence of ${\mathcal X}$ -rectangles disjoint from ${\mathcal Y}$ and vice versa, a hypothesis that complements the hypothesis of Theorem 8.

Theorem 9. Let $A\in SL(2,{\mathbb R})$ be a hyperbolic matrix and ${\mathcal X},{\mathcal Y}$ two disjoint finite $f_{A}$ -invariant sets. Assume that for every $x\in {\mathcal X}$ there exists a positive ${\mathcal X}$ -rectangle with origin x disjoint from $ \tilde {{\mathcal Y}}$ and for every $y\in {\mathcal Y}$ a negative ${\mathcal Y}$ -rectangle with origin y disjoint from $ \tilde {{\mathcal X}}$ . Then there exists $N>0$ such that every Anosov flow of the form ${{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y}, (m_{i})_{i\in I}, (n_{j})_{j\in J})$ with $m_{i}\leq -N$ and $n_{j}\geq N$ is not ${\mathbb R}$ -covered.

Once again the same statement holds by straightforward symmetries.

The hypothesis of Theorem 9 can be satisfied in a great variety of settings. Indeed, in Lemma 8.7 (see also Corollary 8.1) we will give a method for constructing for any $A \in SL(2,{\mathbb R})$ infinitely many pairs $({\mathcal X},{\mathcal Y})$ satisfying this condition.

3 ${\mathbb R}$ -covered and non- ${\mathbb R}$ -covered Anosov flows on $3$ -manifolds

3.1 Anosov flows: definitions, stability, orbital equivalence

Definition 3.1. A $C^{1}$ -vector field X on a closed manifold M is called an Anosov flow if the tangent bundle $TM$ admits a splitting

$$ \begin{align*} TM= E^{s}\oplus {\mathbb R} X\oplus E^{u}\end{align*} $$

satisfying the following properties.

• • The splitting is invariant under the natural action of the derivative $DX^{t}$ of the flow on $TM$ :

  $$ \begin{align*} DX^{t}(E^{s}(x))=E^{s}(X^{t}(x)) \quad\mbox{and}\quad DX^{t}(E^{u}(x))=E^{u}(X^{t}(x)).\end{align*} $$

• • If $\|\cdot \|$ is a Riemannian metric on M, there exist $C>0$ and $0<\lambda <1$ such that, for any $x\in M$ , $t>0$ and any two vectors $u\in E^{s}(x)$ and $v\in E^{u}(x)$ ,

  $$ \begin{align*}\|DX^{t}(u)\|\leq C \lambda^{t}\|u\| \quad\mbox{and}\quad \|DX^{-t}(v)\|\leq C \lambda^{t}\|v\|.\end{align*} $$

An important property of Anosov flows is stated in the following theorem.

Theorem 10. [A] If X is an Anosov flow, then there is $C^{1}$ -neighbourhood ${\mathcal U}$ of X such that every $Y \in {\mathcal U}$ is topologically (orbitally) equivalent to X: there is a homeomorphism $h\colon M\to M$ such that for every $x\in M$ the image of the oriented orbit of X through x is the oriented orbit of Y through $h(x)$ . One says that X is $C^{1}$ -structurally stable .

The homeomorphism h in the theorem can be chosen isotopic to the identity map.

We denote by ${\mathcal A}(M)$ the set of orbital equivalence classes of Anosov flows and by ${\mathcal A}_{0}(M)$ the set of equivalence classes of Anosov flows through orbital equivalence by homeomorphisms isotopic to the identity. Theorem 10 implies that the set ${\mathcal A}_{0}(M)$ is at most countable on any closed manifold M. The set ${\mathcal A}(M)$ , being a quotient of ${\mathcal A}_{0}(M)$ , is at most countable too.

There are simple examples of manifolds M for which ${\mathcal A}_{0}(M)$ is infinite (consider, for instance, the image of the geodesic flow of a hyperbolic surface by a vertical diffeomorphism of the unit tangent bundle). It remains unknown whether there are manifolds for which ${\mathcal A}(M)$ is infinite. There are $3$ -manifolds for which ${\mathcal A}(M)$ has a cardinal greater than any given number, see [BeBoYu]. An example of manifold M for which ${\mathcal A}(M)$ is infinite has recently been proposed in [ClPi].

3.2 Foliations

Another important property of Anosov flows is that the stable, centre stable, unstable and centre unstable fibre bundles $E^{s},E^{cs}=E^{s}\oplus {\mathbb R} X, E^{u}, E^{cu}=E^{u}\oplus {\mathbb R} X$ are uniquely integrable.

Theorem 11. There are unique foliations ${\mathcal F}^{s},{\mathcal F}^{cs}, {\mathcal F}^{u}, {\mathcal F}^{cu}$ tangent to $E^{s},E^{cs}, E^{u}, E^{cu}$ . More precisely any $C^{1}$ curve tangent to one of these bundles is contained in a leaf of the corresponding foliation. These foliations are invariant under the flow of X.

The foliations ${\mathcal F}^{s},{\mathcal F}^{cs}, {\mathcal F}^{u}$ and ${\mathcal F}^{cu}$ are respectively called stable, centre stable, unstable and centre unstable.

In dimension $3$ the centre stable and centre unstable foliations provide the main known obstructions for a $3$ -manifold M to carry an Anosov flow.

Theorem 12. A leaf L of the centre stable (or centre unstable foliation) is:

• • diffeomorphic to a plane ${\mathbb R}^{2}$ if and only if L does not contain a periodic orbit;

• • diffeomorphic to a cylinder ${\mathbb R}\times S^{1}$ if it contains a periodic orbit of X with positive stable eigenvalue—the periodic orbit in L is unique;

• • diffeomorphic to a Möbius band if it contains a periodic orbit with negative stable eigenvalue—again the periodic orbit in L is unique.

As a direct corollary of the above, the manifold M carries foliations ( ${\mathcal F}^{cs}$ and ${\mathcal F}^{cu}$ ) with no compact leaves and thus with no Reeb component. Under these hypotheses, a consequence of Novikov’s theorem implies that M admits ${\mathbb R}^{3}$ as a universal cover.

A simple argument also allows us to check that the leaves have exponential growth. As a consequence of this, the fundamental group of M has exponential growth (see [PlaTh]).

3.3 The bifoliated plane associated to an Anosov flow on a $3$ -manifold, ${\mathbb R}$ -covered and non- ${\mathbb R}$ -covered Anosov flows

Before beginning this section, the reader can refer to §1.2 for the definitions of:

• • the bifoliated plane $({\mathcal P}_{X}, F^{s}_{X},F^{u}_{X})$ associated to an Anosov flow X on a $3$ -manifold;

• • a non- ${\mathbb R}$ -covered Anosov flow;

• • an ${\mathbb R}$ -covered Anosov flow;

• • a twisted ${\mathbb R}$ -covered Anosov flow;

• • a positively and negatively twisted ${\mathbb R}$ -covered Anosov flow (these notions are only defined on oriented manifolds and depend on a choice of the orientation of the manifold).

Any (non-singular) foliation on the plane is orientable and transversally orientable. We will sometimes use a choice of orientation of the foliations $F^{s}_{X}$ , $F^{u}_{X}$ . By convention, in that case the orientation chosen on ${\mathcal P}_{X}$ is the orientation on $F^{s}_{X}$ followed by the orientation on $F^{u}_{X}$ .

As we consider flows X on oriented manifolds M, the normal bundle of X is naturally oriented as follows: the orientation of X followed by the orientation of its normal bundle is the orientation of M. The orientation on ${\mathcal P}_{X}$ can be seen as the orientation of the normal bundle of X.

As M is oriented, the strong stable foliation ${\mathcal F}^{s}_{X}$ is oriented if and only if ${\mathcal F}^{u}_{X}$ is oriented. In that case, by convention, the orientation on ${\mathcal F}^{s}_{X}$ followed by the orientation of ${\mathcal F}^{u}_{X}$ is the normal orientation of the normal bundle of X.

If ${\mathcal F}^{s}_{X}$ and ${\mathcal F}^{u}_{X}$ are not oriented, then their local orientations define a $2$ -fold cover on M and the lift of X on this cover is an Anosov flow with oriented strong stable and strong unstable foliations.

The fundamental group $\pi _{1}(M)$ acts by the deck transformation group on the universal cover $\tilde M\simeq {\mathbb R}^{3}$ of M. This action preserves the lift $\tilde X$ of X on $\tilde M$ and also preserves the lifts $\tilde {\mathcal F}^{cs}_{X},\tilde {\mathcal F}^{cu}_{X}$ of the centre stable and centre unstable foliations. Therefore, the action passes to the quotient by the equivalence relation ‘belonging in the same orbit’. The space obtained by this quotient is ${\mathcal P}_{X}$ and we will denote the projection map by $\pi : \tilde {M}\rightarrow {\mathcal P}_{X}$ . We thus obtain an action of $\pi _{1}(M)$ on ${\mathcal P}_{X}$ , which preserves the foliations $F^{s}_{X}$ and $F^{u}_{X}$ . This action is called the natural action of $\pi _{1}(M)$ on the bifoliated plane $({\mathcal P}_{X}, F^{s}_{X}, F^{u}_{X})$ and we denote it by

$$ \begin{align*}\theta_{X}\colon \pi_{1}(M)\to \mathrm{Homeo}({\mathcal P}_{X}, F^{s}_{X}, F^{u}_{X}),\end{align*} $$

where $\mathrm {Homeo}({\mathcal P}_{X}, F^{s}_{X}, F^{u}_{X})$ is the group of homeomorphisms of the plane ${\mathcal P}_{X}$ preserving the foliations $F^{s}_{X}$ and $F^{u}_{X}$ .

As we consider only Anosov flows on oriented manifolds, the action $\theta _{X}$ takes values in $\mathrm {Homeo}_{+}({\mathcal P}_{X}, F^{s}_{X}, F^{u}_{X})$ and thus preserves the orientation on ${\mathcal P}_{X}$ .

However, $\theta _{X}$ may not preserve the orientations of the foliations $F^{s}_{X}$ and $F^{u}_{X}$ .

If X is a transitive Anosov flow then the action on ${\mathcal P}_{X}$ admits dense orbits. Furthermore, the orbit of any half leaf of $F^{s}_{X}$ and of $F^{u}_{X}$ is dense in ${\mathcal P}_{X}$ .

Let $x_{0}$ be the base point of $\pi _{1}(M)$ in M and $\tilde {x_{0}}$ a lift of $x_{0}$ on $\tilde {M}$ . Consider an element $\tilde \gamma \in {\mathcal P}_{X}$ corresponding to a periodic orbit $\gamma \subset M$ , and $\tilde {\Gamma }$ the lift of $\gamma $ on $\tilde {M}$ corresponding to $\tilde {\gamma }$ . Then one has a well-defined element $[\tilde \gamma ]\in \pi _{1}(M)$ which is the homotopy class of a closed path obtained by the concatenation $\sigma \gamma \sigma ^{-1}$ , where $\sigma $ is the projection on M of a path in $\tilde {M}$ joining $\tilde {x_{0}}$ to a point of the orbit $\tilde \Gamma $ .

The following lemma is a classical result in the theory (see, for instance, [Ba]).

Lemma 3.1. Let $\tilde \gamma \in {\mathcal P}_{X}$ be a point corresponding to a periodic orbit $\gamma $ of X. Consider $G_{\tilde \gamma }\subset \pi _{1}(M)$ its stabilizer for the natural action of $\theta $ . Then $G_{\tilde \gamma }$ is the cyclic group generated by the homotopy class $[\tilde \gamma ]$ .

Using the previous notation, we say that a curve $L^{s}\subset W^{s}(\gamma )$ is a complete (stable) transversal if it is transverse to X, cuts all the orbits in $W^{s}(\gamma )$ and also is such that the first return map of X induces a homeomorphism $P_{\gamma }\colon L^{s}\to L^{s}$ (which is a contraction). One defines in the same way a complete (unstable) transversal $L^{u} \subset W^{u}(\gamma )$ and the first return map $P_{\gamma }\colon L^{u}\to L^{u}$ (which is a dilation).

Take complete stable and unstable transversals $L^{s}$ and $L^{u}$ that contain a point $x\in \gamma $ . Now using the previous notation, take any lift $\tilde {x}$ of x in $\tilde {\Gamma }$ . $L^{s}$ and $L^{u}$ admit canonical lifts $L^{s}_{\tilde x}$ and $L^{u}_{\tilde x}$ on $\tilde M$ through $\tilde {x}$ . Let us denote the lift maps by $\pi ^{s}_{\tilde {x}}: L^{s} \rightarrow L^{s}_{\tilde x}$ and $\pi ^{u}_{\tilde {x}}: L^{u} \rightarrow L^{u}_{\tilde x}$ . $L^{s}_{\tilde x}$ and $L^{u}_{\tilde x}$ project on ${\mathcal P}_{X}$ injectively. We can therefore define two bijections $h^{s}:=\pi \circ \pi ^{s}_{\tilde {x}}$ and $h^{u}:=\pi \circ \pi ^{u}_{\tilde {x}}$ from $L^{s}$ and $L^{u}$ to $F_{X}^{s}(\gamma )$ and $F_{X}^{u}(\gamma )$ . We denote by $P_{\tilde \gamma }\colon F^{s}_{X}(\tilde \gamma )\to F^{s}_{X}(\tilde \gamma )$ and $P_{\tilde \gamma }\colon F^{u}_{X}(\tilde \gamma )\to F^{u}_{X}(\tilde \gamma )$ the homeomorphisms $h^{s} P_{\gamma } (h^{s})^{-1}$ and $h^{u} P_{\gamma } (h^{u})^{-1}$ . We can easily convince ourselves that the following lemma holds.

Lemma 3.2. The homeomorphism $P_{\tilde \gamma }\colon F^{s}_{X}(\tilde \gamma )\cup F^{u}_{X}(\tilde \gamma )\to F^{s}_{X}(\tilde \gamma )\cup F^{u}_{X}(\tilde \gamma )$ is independent of the choices of $\tilde x$ , of $L^{s}$ and $L^{u}$ , and is called the first return map of X.

Lemma 3.2 is a consequence of the following lemma.

Lemma 3.3. The natural action $\theta _{X,[\tilde \gamma ]}$ of $[\tilde \gamma ]$ on ${\mathcal P}_{X}$ preserves $F^{s}(\tilde \gamma )$ and $F^{u}(\tilde \gamma )$ and its restriction to $F^{s}(\tilde \gamma )\cup F^{u}(\tilde \gamma )$ is $P_{\tilde \gamma }^{-1}$ .

A proof of Lemma 3.3 can be found in [Ba].

3.4 A characterization of ${\mathbb R}$ -covered Anosov flows by complete and incomplete quadrants

In this section, each time we consider an Anosov flow X, we will assume that the bifoliated plane ${\mathcal P}_{X}$ is endowed with a choice of orientation of the foliations $F^{s}_{X},F^{u}_{X}$ .

Let $({\mathcal F},{\mathcal G})$ be two oriented transverse foliations on the plane ${\mathcal P}={\mathbb R}^{2}$ . This defines four quadrants at each point x: for any $\omega =(\omega _{1},\omega _{2})\in \{-,+\}^{2}$ , the (closed) quadrant $C_{\omega }(x)$ is the closure of the connected component of ${\mathcal P}\setminus ({\mathcal F}(x)\cup {\mathcal G}(x))$ bounded by the half leaves ${\mathcal F}_{\omega _{1}}(x),{\mathcal G}_{\omega _{2}}(x)$ .

Definition 3.2.

• • We say that the pair $({\mathcal F}, {\mathcal G})$ is undertwisted or incomplete in the quadrant $C_{(+,+)}(x)$ if there are $y\in {\mathcal F}^{+}(x)$ and $z\in {\mathcal G}^{+}(x)$ such that

  $$ \begin{align*}{\mathcal G}^{+}(y)\cap{\mathcal F}^{+}(z)=\emptyset.\end{align*} $$

• • We say that the pair $({\mathcal F}, {\mathcal G})$ is complete (or has the complete intersection property) in the quadrant $C_{(+,+)}(x)$ if for all $y\in {\mathcal F}^{+}(x)$ and $z\in {\mathcal G}^{+}(x)$ ,

  $$ \begin{align*}{\mathcal G}^{+}(y)\cap{\mathcal F}^{+}(z)\neq \emptyset.\end{align*} $$

The complete case is divided into two subcases.

• • $({\mathcal F},{\mathcal G})$ is trivial in the quadrant $C_{+,+}(x)$ if

  $$ \begin{align*} \bigcup_{y\in {\mathcal F}_{+}(x)}{\mathcal G}_{+}(y)=\bigcup_{z\in {\mathcal G}_{+}(x)}{\mathcal F}_{+}(z). \end{align*} $$

• • The pair $({\mathcal F},{\mathcal G})$ is overtwisted in the quadrant $C_{+,+}(x)$ if it is complete but not trivial. In other words, for all $y\in {\mathcal F}^{+}(x)$ and $z\in {\mathcal G}^{+}(x)$ , we have ${\mathcal G}^{+}(y)\cap {\mathcal F}^{+}(z)\neq \emptyset $ , but there is $p\in C_{+,+}(x)$ such that ${\mathcal F}(x)\cap {\mathcal G}(p)=\emptyset $ or ${\mathcal G}(x)\cap {\mathcal F}(p)=\emptyset $ .

One defines these notions in all the other quadrants in the same way, changing some $+$ into $-$ according to the quadrant.

Remark 3.1.

• • If X is a suspension, every quadrant is trivial.

• • If X is ${\mathbb R}$ -covered and positively twisted, then the quadrants $C_{+,+}(x)$ , $C_{-,-}(x)$ are complete and overtwisted, and the quadrants $C_{+,-}(x) C_{-,+}(x)$ are undertwisted.

• • If X is ${\mathbb R}$ covered and negatively twisted, then the quadrants $C_{+,-}(x)$ , $C_{-,+}(x)$ are complete and overtwisted and the quadrants $C_{+,+}(x) C_{-,-}(x)$ are undertwisted.

Lemma 3.4. Let $({\mathcal F},{\mathcal G})$ be a pair of oriented transverse foliations and assume that two leaves $L_{1}$ and $L_{2}$ in ${\mathcal F}$ are not separated from above, that is. there are two positively oriented ${\mathcal G}$ -leaf segments $\sigma _{i}\colon [0,1]\to {\mathcal P}$ such that $\sigma _{i}(0)\in L_{i}$ and $\sigma _{1}(t)$ and $\sigma _{2}(t)$ belong to the same ${\mathcal F}$ -leaf for all $t>0$ . Then there exist $x,y\in {\mathcal P}$ such that $C_{-,-}(x)$ and $C_{+,-}(y)$ are incomplete (undertwisted).

Proof. It suffices to take $x=\sigma _{i}(t)$ and $y=\sigma _{j}(t)$ for some $t>0$ (see Figure 4).

Lemma 3.5. A transitive Anosov flow X is a suspension if and only if there exist $x\in {\mathcal P}_{X}$ and $\omega \in \{+,-\}^{2}$ such that the quadrants $C_{\omega }(x)$ and $C_{-\omega }(x)$ are trivially foliated.

Figure 4 In this figure the white circle should be considered as a point at infinity.

Proof. An Anosov suspension flow has clearly trivially foliated quadrants; we only need to prove the converse. Since being or not being a suspension is invariant by finite covers, up to considering the lift of X on the $2$ -fold cover of the orientation of the stable/unstable bundles, we will assume that the stable/unstable bundles of X are orientable.

Assume that X is a transitive Anosov flow, whose bifoliated plane has a trivial quadrant, say $C_{+,+}(x)$ . Note that $C_{+,+}(y)$ is trivial too for any $y\in C_{+,+}(x)$ . As X is transitive, there exists $y\in C_{+,+}(x)$ with a dense orbit. One deduces that for any $z\in {\mathcal P}_{X}$ , there is $\gamma \in \pi _{1}(M)$ such that $z\in C_{+,+}(\theta _{\gamma }(y))$ . Thus $C_{+,+}(z)$ is trivial for any $z\in {\mathcal P}(x)$ . Of course, by exactly the same method, we obtain that $C_{-,-}(z)$ is also trivial for any $z\in {\mathcal P}(x)$ .

Therefore, thanks to Lemma 3.4, $F^{s}_{X}$ and $F^{u}_{X}$ do not contain non-separated leaves, hence X is ${\mathbb R}$ -covered. Finally, by Remark 3.1 it cannot be twisted, so the bifoliated plane is trivial and X is a suspension.

By Remark 3.1 and Lemma 3.4, we get the following criteria for deciding whether an Anosov flow is ${\mathbb R}$ -covered or not.

Corollary 3.1. An Anosov flow X is not ${\mathbb R}$ -covered if and only if there are $x,y\in {\mathcal P}_{X}$ and $\omega _{x},\omega _{y}\in \{-,+\}^{2}$ which are adjacent (that is, distinct and not opposite) such that the quadrants $C_{\omega _{x}}(x)$ and $C_{\omega _{y}}(y)$ are incomplete.

Corollary 3.2. Let X be an Anosov flow and assume that for every $x\in {\mathcal P}_{X}$ the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ are complete. Then either the bifoliation is trivial or the flow is ${\mathbb R}$ -covered and positively twisted.

Remark 3.2. Given a transitive Anosov flow X, the set of $x\in {\mathcal P}_{X}$ such that the pair $(F^{s}_{X},F^{u}_{X})$ is incomplete in $C_{(+,+)}(x)$ is either empty or a dense open subset.

3.5 Stable and unstable holonomies and the completeness of the quadrants

Fix $x\in {\mathcal P}_{X}$ and consider $y\in F^{u}_{X}(x)$ . We call the map $h^{u}_{X,x,y}$ from $F^{s}_{X}(x)$ to $F^{s}_{X}(y)$ defined by

$$ \begin{align*}\{h^{u}_{X,x,y}(z)\}= F^{u}_{X}(z)\cap F^{s}_{X}(y),\quad\mbox{for } z\in F^{s}_{X}(x), \quad\mbox{if } F^{u}_{X}(z)\cap F^{s}_{X}(y)\neq \emptyset\end{align*} $$

an unstable holonomy from x to y. This definition is consistent as the intersection of a stable and an unstable leaves is at most one point.

The domain ${\mathcal D}(h^{u}_{X,x,y})$ is an interval of $F^{s}_{X}(x)$ and the image is an interval of $F^{s}_{X}(y)$ .

One defines in a analogous way the stable holonomy $h^{s}_{X,x,z}$ for $z\in F_{X}^{s}(x)$ .

Remark 3.3. For $x\in {\mathcal P}_{X}$ the quadrant $C_{+,+}(x)$ is complete if for any $y\in F^{u}_{+}(x)$ one has

$$ \begin{align*}F^{s}_{+}(x)\subset {\mathcal D}(h^{u}_{X,x,y}).\end{align*} $$

The quadrant $C_{+,+}(x)$ is undertwisted if there is $y\in F^{u}_{+}(x)$ such that ${\mathcal D}(h^{u}_{X,x,y})$ is a relatively compact interval in $F^{s}_{+}(x)$ .

Analogous statements hold in every quadrant and by exchanging the unstable holonomy for the stable holonomy.

3.6 Dehn–Goodman–Fried surgery

As explained in the introduction, it has recently been proven that the topological flow built by Fried’s surgery is orbitally equivalent to the Anosov flow obtained by Goodman’s surgery. Thanks to its explicitness, throughout the next pages we will make use of the action of Fried’s surgery on the bifoliated plane rather than its general definition which we quickly recall now.

Let X be an Anosov flow on a oriented $3$ -manifold M and let $\gamma $ be a periodic orbit with positive eigenvalues.

Consider the blow-up $\pi _{\gamma }\colon M_{\gamma }\to M$ of M along $\gamma $ , that is:

• • $M_{\gamma }$ is a manifold with boundary and $\partial M_{\gamma }$ is a torus $T_{\gamma } \simeq {\mathbb T}^{2}$ ;

• • $\pi _{\gamma }$ induces a diffeomorphism from the interior of $M_{\gamma }$ to $M\setminus \gamma $ ;

• • for every $x\in \gamma $ the fibre $\pi _{\gamma }^{-1}$ is a circle which is canonically identified with the unit normal bundle $N^{1}(x)$ of $\gamma $ in M at the point x.

In other words, consider two segments $\sigma _{1},\sigma _{2}$ in $M_{\gamma }$ transverse to the boundary $\partial M_{\gamma }$ at $\sigma _{i}(0)$ . Then $\sigma _{1}(0)=\sigma _{2}(0)$ if and only if $\pi _{\gamma }(\sigma _{1}(0))=\pi _{\gamma }(\sigma _{2}(0))=c$ and the segments $c_{1}=\pi _{\gamma }\circ \sigma _{1}$ and $c_{2}=\pi _{\gamma }\circ \sigma _{2}$ have the following property: the vector $({\partial c_{2}}/{\partial t})(0)$ belongs to the half plane of $T_{c(0)}M$ containing $\pm X(c(0))$ and $({\partial c_{1}}/{\partial t})(0)$ .

The vector field $\pi _{\gamma }^{-1}(X)$ is well defined on the interior of $M_{\gamma }$ , and extends by continuity on the boundary $T_{\gamma }$ by the natural action of the derivative $DX^{t}$ on the normal bundle over $\gamma $ . We denote by $X_{\gamma }$ this (smooth) vector field on $M_{\gamma }$ .

The flow on $T_{\gamma }$ is a Morse–Smale flow with four periodic orbits, which correspond to the normal vectors to $\gamma $ tangent to the stable and unstable manifolds of $\gamma $ . These four periodic orbits are freely homotopic to one another and are non-trivial in $\pi _{1}(T_{\gamma })$ . The homotopy (or homology) class $b\in {\mathbb Z}^{2}=\pi _{1}(T_{\gamma })$ of these periodic orbits is called the parallel.

On the other hand, the fibres of $\pi _{\gamma }\colon T_{\gamma }\to \gamma $ inherit an orientation from the orientation of M, and the corresponding homotopy class $a\in {\mathbb Z}^{2}=\pi _{1}(T_{\gamma })$ is called the meridian.

Given any integer $n\in {\mathbb Z}$ , one easily checks the existence of foliations ${\mathcal G}_{n}$ on $T_{\gamma }$ , transverse to the flow $X_{\gamma }$ , whose leaves are simple closed curves of homotopy class $a+nb$ . By reparametrizing the flow $X_{\gamma }$ , one gets a new smooth vector field $Y_{\gamma }$ on $M_{\gamma }$ that leaves the foliation ${\mathcal G}_{n}$ invariant.

Let $M_{\gamma ,n}$ be the manifold obtained from $M_{\gamma }$ by collapsing the leaves of ${\mathcal G}_{n}$ . The flow $Y_{\gamma }$ passes to the quotient and becomes a topological Anosov flow $X_{\gamma ,n}$ on $M_{\gamma ,n}$ .

It is easy to do this construction in a way such that $X_{\gamma ,n}$ is a Lipschitz vector field, but it is not clear at all that it can be smooth and Anosov. It is not even clear that the orbital equivalence class of the construction does not depend on the choice of the foliation ${\mathcal G}_{n}$ . Shannon proved that it is orbitally equivalent (by a homeomorphism isotopic to the identity) to an Anosov flow (the one built by Goodman), proving at the same time that the orbital equivalence class of this construction (in fact, the element of ${\mathcal A}_{0}(M_{\gamma ,n})$ ) is well defined. This element of ${\mathcal A}_{0}(M_{\gamma ,n})$ is called the Anosov flow $X_{\gamma ,n}$ obtained from Xby a surgery along $\gamma $ with characteristic number n.

Remark 3.4.

• • If $\gamma _{1},\gamma _{2}$ are periodic orbits of X and $n_{1},n_{2}$ are integers, then

  $$ \begin{align*}[X_{\gamma_{1},n_{1}}]_{\gamma_{2},n_{2}}=[X_{\gamma_{2},n_{2}}]_{\gamma_{1},n_{1}}.\end{align*} $$
  In other words, the surgeries are commutative operations. This allows us to speak without any ambiguity of the Anosov vector field Y obtained from X by performing surgeries along periodic orbits $\gamma _{1},\ldots ,\gamma _{k}$ with characteristic numbers $n_{1},\ldots ,n_{k}$ .

• • If $\gamma $ is a periodic orbit and $m,n\in {\mathbb Z}$ then

  $$ \begin{align*}[X_{\gamma,m}]_{n}=X_{\gamma,m+n}.\end{align*} $$

3.6.1 Dehn–Goodman–Fried surgeries along orbits with negative eigenvalues

On an orientated $3$ -manifold, Dehn–Goodman–Fried surgeries can be performed on periodic orbits $\gamma $ with two negative eigenvalues $-\lambda $ and $-( 1/\lambda )$ , for $\lambda>1$ . However, the parallel and meridian intersect twice and thus are not a basis of $\pi _{1}(T_{\gamma })$ . This leads to some restrictions that we explain below.

More precisely, the boundary of a tubular neighbourhood of $\gamma $ is still a torus $T_{\gamma }$ endowed with a meridian $a\in \pi _{1}(T_{\gamma })$ and carrying a Morse–Smale flow with two periodic orbits (one attractor and one repeller) which are in the same homotopy class b called a parallel.

The intersection number of the meridian with the parallel is $a\cdot b=2$ .

The loop $a+kb$ is a multiple of $2$ in $\pi _{1}(T_{\gamma })$ for any odd k and therefore cannot be used as a new parallel. However, one can perform a Fried surgery corresponding to keeping the parallel b and replacing the meridian by $a+2kb$ , $k\in {\mathbb Z}$ . The number k will be called the characteristic number of the surgery.

We can visualize this surgery on the $2$ -fold cover $\hat M\to M$ of the orientations of the stable/unstable bundles, endowed with the lift $\hat X$ of X. The orbit $\gamma $ lifts to a periodic orbit $\hat \gamma $ whose period is twice the period of $\gamma $ and whose eigenvalues are $\lambda ^{-2}<1<\lambda ^{2}$ . The natural projection $T_{\hat \gamma }\to T_{\gamma }$ maps the meridian and the parallel of $T_{\hat \gamma }$ on those of $T_{\gamma }$ .

The surgery on M along $\gamma $ with characteristic number k is the quotient of a surgery on $\hat M$ , with characteristic number $2k$ : one can realize it by performing two Goodman surgeries with characteristic number k along two annuli in opposite quadrants of the tubular neighbourhood of $\hat \gamma $ which are images of each other by an element of the deck transformation group.

Remark 3.5.

• • Dehn–Goodman surgery is a local construction and thus can be done on non-orientable manifolds for orientation-preserving periodic orbits. However, the characteristic number depends on the local orientation and thus is not well defined for non-orientable manifolds.

• • The boundary of the tubular neighbourhood of a non-orientable periodic orbit is a Klein bottle, on which the (non-oriented) meridian is canonically defined. Thus, there are no possible Dehn–Goodman surgeries along such orbits.

3.6.2 Fried surgeries leading to hyperbolic manifolds

In this article we are interested in constructing Anosov flows on hyperbolic manifolds. There are two reasons for this. First. Anosov flows on hyperbolic manifolds satisfy additional structural properties; for instance any periodic orbit of any ${\mathbb R}$ -covered Anosov flow on a hyperbolic manifold is freely homotopic to infinitely many periodic orbits (see [Fe1]). Second, we wish to enrich the list of examples of non- ${\mathbb R}$ -covered Anosov flows on hyperbolic manifolds. To our knowledge, the only examples of such flows have been constructed in [Fe2] and more recently in a draft by Béguin and Yu.

In this paper, we provide a construction of infinitely many ${\mathbb R}$ -covered and non- ${\mathbb R}$ -covered Anosov flows on hyperbolic manifolds. The most important step of the hyperbolic part of the construction, which also proves the addenda of Theorems 6 and 7, is the following lemma.

Lemma 3.6. Let X be the suspension flow of an Anosov diffeomorphism of the torus ${\mathbb T}^{2}$ and M its underlying manifold. Fix periodic orbits $\gamma _{1},\ldots ,\gamma _{n}$ of X. There exist finite subsets $D_{1}, \ldots , D_{n}$ of $\mathbb {Z}$ such that for any $(k_{1},\ldots ,k_{n}) \in {\mathbb Z}^{n}- [(D_{1}\times {\mathbb Z}^{n-1}) \cup ({\mathbb Z} \times D_{2} \times {\mathbb Z}^{n-2}) \cdots \cup ({\mathbb Z}^{n-1} \times D_{n})]$ , $[[[X_{\gamma _{1},k_{1}}]_{\gamma _{2},k_{2}}]\cdots ]_{\gamma _{n},k_{n}}$ is an Anosov flow on a hyperbolic manifold.

Proof. In [Th] Thurston showed that $M -\bigcup _{i=1}^{n}\gamma _{i}$ admits a complete hyperbolic structure of finite volume, and thanks to the hyperbolic Dehn surgery theorem (see [Th1]) we obtain the desired result.

4 The surgeries and the bifoliated plane

Let X and Y be two Anosov flows on closed $3$ -manifolds M and N such that (the orbital equivalence class of) Y is obtained from X by performing finitely many surgeries along periodic orbits: there exist $k\in {\mathbb N}$ , a finite set $\Gamma =\{\gamma _{1},\ldots ,\gamma _{k}\}$ of periodic orbits of X and a finite set ${\mathcal N}=\{n_{1},\ldots ,n_{k}\}\subset {\mathbb Z}$ such that $Y= X_{\Gamma ,{\mathcal N}}$ , that is, Y is the topological Anosov flow obtained from X by performing a Fried surgery with characteristic number $n_{i}$ on each $\gamma _{i}$ .

The aim of this section is to give a very partial answer to the following question.

Question 4.1. Knowing the bifoliated plane $({\mathcal P}_{X},F^{s}_{X},F^{u}_{X})$ , what can we say about $({\mathcal P}_{Y}, F^{s}_{Y},F^{u}_{Y})$ ?

A key remark for answering this question is that $\Gamma $ can be considered as a subset of N and

$$ \begin{align*}M\setminus \Gamma = N\setminus \Gamma \quad\mbox{and}\quad X|_{M\setminus \Gamma}= Y|_{N\setminus \Gamma}.\end{align*} $$

Remark 4.1. If $\Gamma $ contains orbits with negative eigenvalues, we can replace X and Y by their lifts $\hat X$ , $\hat Y$ on the $2$ -fold covers $\hat M$ , $\hat N$ corresponding to the orientations of their foliations. Let $\hat \Gamma $ be the lift of $\Gamma $ on $\hat M$ . Then, according to §3.6.1, $\hat Y$ is obtained from $\hat X$ by performing surgeries along the orbits $\hat \gamma \in \hat \Gamma $ with characteristic number $\hat n(\hat \gamma )$ defined as follows:

• • if $\hat \gamma $ projects on M to an orbit $\gamma _{i}$ with positive eigenvalues, then $\hat n(\hat \gamma )= n_{i}$ ;

• • if $\hat \gamma $ projects on M to an orbit $\gamma _{i}$ with negative eigenvalues, then $\hat n(\hat \gamma )= 2n_{i}$ .

Recall that the bifoliated planes of X and Y are the same as those of $\hat X$ and $\hat Y$ , respectively. Therefore, in order to understand the effect of surgeries on the bifoliated plane, it suffices to consider vector fields with transversally oriented foliations.

In view of Remark 4.1 above, from now until Theorem 13, we will assume that the eigenvalues of the $\gamma _{i}$ are positive. We explain how to adapt the statement of Theorem 13 to the case of negative eigenvalues in Remark 4.6.

In what follows the bifoliated plane ${\mathcal P}_{X}$ will be always endowed with an orientation of the foliations $F^{s}_{X}$ and $F^{u}_{X}$ .

4.1 The key tool: a common cover

We will denote by $\tilde \Gamma _{X}\subset \tilde M$ and $\tilde \Gamma _{Y}\subset \tilde N$ the lifts of $\Gamma $ to the universal covers $\tilde M$ and $\tilde N$ .

By a convenient abuse of language, we will also denote by $\tilde \Gamma _{X}$ and $\tilde \Gamma _{Y}$ the corresponding (discrete) sets in ${\mathcal P}_{X}$ and ${\mathcal P}_{Y}$ .

Let $V=M\setminus \Gamma =N\setminus \Gamma $ and Z be the restriction of X to V (or equivalently of Y to V).

Claim 1. The universal cover $(\tilde V,\tilde Z)$ is conjugated to $({\mathbb R}^{3},\partial /\partial x)$ ,

Proof. $\tilde V$ is the universal cover of $\tilde M\setminus \tilde \Gamma _{X}$ which is conjugated to ${\mathbb R}^{3}$ minus a discrete family of orbits of $\partial /\partial x$ which are parallel straight lines.

The space of orbits in $\tilde V$ is a bifoliated plane, denoted by $({\mathcal P}_{\Gamma }, F^{s}_{\Gamma }, F^{u}_{\Gamma })$ . This bifoliated plane is the universal cover of $({\mathcal P}_{X},F^{s}_{X},F^{u}_{X})\setminus \tilde \Gamma _{X}$ and of $({\mathcal P}_{Y},F^{s}_{Y},F^{u}_{Y})\setminus \tilde \Gamma _{Y}$ . We denote by $\Pi _{X}$ and $\Pi _{Y}$ the natural projections of $\tilde V$ onto ${\mathcal P}_{X}$ and ${\mathcal P}_{Y}$ :

$$ \begin{align*} \begin{array}{rcccl} & &{\mathcal P}_{\Gamma} & & \\ &\overset{\Pi_{X}\;\;\;}\swarrow& &\overset{\;\;\;\Pi_{Y}}\searrow& \\ {\mathcal P}_{X}\setminus \tilde \Gamma_{X}& & & &{\mathcal P}_{Y}\setminus\tilde{\Gamma}_{Y} \end{array} \end{align*} $$

This simple fact has an important (straightforward) consequence.

Lemma 4.1. Let $R_{X}\subset {\mathcal P}_{X}$ be a rectangle for $(F^{s}_{X},F^{u}_{X})$ disjoint from $\tilde \Gamma _{X}$ , and let $R_{\Gamma }$ be a connected component of $\Pi _{X}^{-1}(R_{X})$ . Then $R_{Y}= \Pi _{Y}(R_{\Gamma })$ is a rectangle for $F^{s}_{Y},F^{u}_{Y}$ and $\Pi _{Y}\circ \Pi _{X}^{-1}$ induces a homeomorphism from $R_{X}$ to $R_{Y}$ conjugating $(F^{s}_{X},F^{u}_{X})$ and $(F^{s}_{Y},F^{u}_{Y})$ .

Proof. $R_{\Gamma }$ is a rectangle and $\Pi _{X}$ takes the bifoliated $R_{\Gamma }$ to the bifoliated $R_{X}$ . The only thing to check now is that $\Pi _{Y}$ restricted to $R_{\Gamma }$ is a homeomorphism. It suffices to prove that $\Pi _{Y}$ is injective on the rectangle $R_{\Gamma }$ . If $\Pi _{Y}(x)=\Pi _{Y}(y)$ for $x\neq y\in R_{\Gamma }$ , then the stable and unstable leaves at $\Pi _{Y}(x)$ intersect twice, which is impossible in a (non-singular) bifoliated plane.

One can use the following generalization of this argument.

Proposition 4.1. Consider a closed domain $\Delta _{X}\subset {\mathcal P}_{X}$ such that its interior is disjoint from $\tilde \Gamma _{X}$ and $(\Delta _{X}, F^{s}_{X}|_{\Delta _{X}},F^{u}_{X}|_{\Delta _{X}})$ is conjugated to the trivially bifoliated plane ${\mathbb R}^{2}$ . Let $\Delta _{\Gamma }$ be a connected component of $\Pi _{X}^{-1}(\Delta _{X})$ and let $\Delta _{Y}$ be the closure of $\Pi _{Y}(\Delta _{\Gamma })$ . Then $\Pi _{Y}\circ \Pi _{X}^{-1}$ (defined on $\Delta _{X}\setminus \tilde \Gamma _{X}$ ) extends on $\Delta _{X}$ to a homeomorphism conjugating $(F^{s}_{X},F^{u}_{X})$ to $(F^{s}_{Y},F^{u}_{Y})$ .

4.2 Two ways to associate a path in ${\mathcal P}_{X}$ to a path in ${\mathcal P}_{Y}$

Let $\sigma _{X}\colon {\mathbb R} \to {\mathcal P}_{X}$ be a locally injective continuous path, obtained by the concatenation of locally finitely many stable/unstable leaf segments. One can define a transverse orientation as follows: the transverse orientation followed by the orientation of $\sigma _{X}$ is the orientation of ${\mathcal P}_{X}$ .

Remark 4.2. For this choice of the orientation,

• • the transverse orientation of a positively oriented unstable segment coincides with the orientation of the stable leaves intersecting it, and

• • the transverse orientation of a positively oriented stable segment coincides with the negative orientation of the unstable leaves intersecting it.

Assume that $p_{X}= \sigma _{X}(0) \notin \tilde \Gamma _{X}$ and $p_{Y}\in \Pi _{Y}(\Pi _{X}^{-1}(p_{X}))$ .

Let $\sigma _{X,t}\colon {\mathbb R} \to {\mathcal P}_{X}$ , $t\in [-1,1)$ be a continuous family of paths such that:

• • $\sigma _{X,0}=\sigma _{X}$ ;

• • $\sigma _{X,t}(0)=p_{X}$ ;

• • $\sigma _{X,t}$ is disjoint from $\tilde {\Gamma }_{X}$ ;

• • $\sigma _{X,t}$ tends to $\sigma _{X,0}$ from the positive side as $t\to 0$ and $t>0$ and from the negative side as $t\to 0$ and $t<0$ .

Corollary 4.1. Using the above notation, there are uniquely defined paths $\sigma _{Y,t}$ for $t>0$ (respectively, $t<0$ ) such that

• • $\sigma _{Y,t}(0)=p_{Y}$ , and

• • $\sigma _{Y,t}(s)\in \Pi _{Y}(\Pi _{X}^{-1}(\sigma _{X,t}(s)))$ , $s\in {\mathbb R}$ ,

and the limits

$$ \begin{align*}\lim_{t\to 0_{+}}\sigma_{Y,t}(s)=\sigma_{Y,+}(s) \quad\mbox{and}\quad\lim_{t\to 0_{-}}\sigma_{Y,t}(s)=\sigma_{Y,-}(s)\end{align*} $$

are well-defined continuous paths which are a concatenation of locally finitely many stable/unstable segments. Furthermore, $\sigma _{Y,+}$ and $\sigma _{Y,-}$ only depend on the choice of $p_{Y}$ and not on the choice of the homotopies $\sigma _{X,t}$ .

Proof. We construct $\sigma _{Y,t}$ by lifting $\sigma _{X,t}$ on ${\mathcal P}_{\Gamma }$ , which is the universal cover of ${\mathcal P}_{X}\setminus \tilde {\Gamma }_{X}$ , and then projecting the lifts by $\Pi _{Y}$ on ${\mathcal P}_{Y}\setminus \tilde {\Gamma }_{Y}$ .

The second part of the statement is a consequence of Proposition 4.1.

Definition 4.1. Using the above notation, $\sigma _{Y,+}$ and $\sigma _{Y,-}$ are respectively called the positive and negative paths through $p_{Y}$ corresponding to $\sigma _{X}$ . We can similarly define this notion in the case where $p_{X}\in \tilde {\Gamma }_{X}$ .

It is fairly easy to see that, in general, $\sigma _{Y,+}$ and $\sigma _{Y,-}$ do not coincide. An example of such a case is given in Figure 5. In this example, we consider a black path and a family of green and blue paths all with the same endpoints in ${\mathcal P}_{X}$ . Because of the surgery performed on p, by applying $\Pi _{Y} \circ \Pi _{X}^{-1}$ to a blue and a green path, we obtain two paths in ${\mathcal P}_{Y}$ that do not share the same endpoints. This is made more precise in Proposition 4.2.

Figure 5 In this picture the black points represent points in $\tilde {\Gamma }_{X,Y}$ on which we have performed non-trivial surgeries. Colour available online.

4.3 Comparison of holonomies: the main tool

Recall that, given an Anosov flow X, the orientations of the manifold M, of the bifoliated plane ${\mathcal P}_{X}$ and the foliations $F^{s}_{X}$ and $F^{u}_{X}$ are related by the convention introduced in §3.3.

Our main tool for comparing the holonomies of the foliations associated to X and Y is the next proposition.

Proposition 4.2. Let $\tilde \gamma \in {\mathcal P}_{X}$ be a point corresponding to a periodic orbit $\gamma \in \Gamma $ . Let n be the characteristic number of the surgery performed on $\gamma $ . Consider two rectangles $R^{+},R^{-}$ such that the following statements hold.

• • $R^{\pm }\cap \tilde \Gamma _{X}=\{\tilde \gamma \}$ .

• • $\tilde \gamma $ belongs to the interior of the lower stable boundary component $J^{s}$ of $R^{+}$ (see Figure 6) and to the interior of the upper stable boundary component $I^{s}$ of $R^{-}$ .

  

  Figure 6 The action of a surgery on two adjacent rectangles: the union of $R^+$ and $R^-$ in ${\mathcal P}_X$ , which is not a rectangle, corresponds to a rectangle of ${\mathcal P}_Y$ . Colour available online.

• • The positively oriented stable segments $I^{s},J^{s}$ satisfy $I^{s}=[a,b]^{s}$ and $J^{s}=[a,c]^{s}$ , with $c= P_{\tilde \gamma }^{n}(b)$ , where $P_{\tilde \gamma }$ is the first return map on $F^{s}(\tilde \gamma )$ and $F^{u}(\tilde \gamma )$ .

If we denote $R^{\pm }=R^{+} \cup R^{-}$ , then for any connected component $R^{\pm }_{\Gamma }$ of $\Pi _{X}^{-1}(R^{\pm })$ the projection $\Pi _{Y}(R^{\pm }_{\Gamma })$ is a rectangle punctured at $\tilde \gamma $ .

Proof. Consider the closed curve $\delta $ on ${\mathcal P}_{X}$ starting at the point c, following $\partial R^{+}\setminus Int (J^{s})$ until a and then following $\partial R^{-}\setminus Int (I^{s})$ until b. Project $\delta $ on a local section of $\gamma $ and complete it by the orbit segment joining b to c. Then the closed curve obtained is freely homotopic in $M\setminus \gamma $ to a meridian plus n parallels of $\gamma $ , that is, to the new meridian after surgery.

Thus $\delta $ is $0$ -homotopic on the manifold N carrying Y. Its lifts on ${\mathcal P}_{Y}$ are closed curves consisting of two stable and two unstable segments, hence bounding a rectangle, which finishes the proof.

In Proposition 4.2 one considers an orbit segment joining the points $b,c \in F^{s}_{+}(\tilde \gamma ) $ by turning around $\tilde \gamma $ in the positive sense. Analogous statements hold after changing the sign of the exponent of the first return map. Let us be more explicit, as this is crucial for our arguments.

Proposition 4.3. Let $\tilde \gamma \in {\mathcal P}_{X}$ be a point corresponding to a periodic orbit $\gamma \in \Gamma $ . Let n be the characteristic number of the surgery performed on $\gamma $ . Consider two rectangles $R^{+},R^{-}$ such that the following statements hold.

• • $R^{\pm }\cap \tilde \Gamma _{X}=\{\tilde \gamma \}$ .

• • $\tilde \gamma $ belongs to the interior of the lower stable boundary component $J^{s}$ of $R^{+}$ and to the interior of the upper stable boundary component $I^{s}$ of $R^{-}$ .

• • The positively oriented stable segments $I^{s},J^{s}$ satisfy $I^{s}=[b,a]^{s}$ and $J^{s}=[c,a]^{s}$ , with $c= P_{\tilde \gamma }^{-n}(b)$ , where $P_{\tilde \gamma }$ is the first return map on $F^{s}(\tilde \gamma )$ and $F^{u}(\tilde \gamma )$ .

If we denote $R^{\pm }=R^{+}\cup R^{-}$ , then for any connected component $R^{\pm }_{\Gamma }$ of $\Pi _{\Gamma }^{-1}(R^{\pm })$ the projection $\Pi _{Y}(R^{\pm }_{\Gamma })$ is a rectangle punctured at $\tilde \gamma $ .

Proof. The proof is identical to that of Proposition 4.2, except that in this case the path from c to b is negatively oriented: one obtains $-1$ meridian minus n parallels for X, which is $-1$ meridian for Y.

Finally, let us note that the previous results hold independently of the sign of the eigenvalues of $\gamma $ .

4.4 Comparison of the holonomies in the quadrants: choosing the holonomies to be compared

Our next goal in this paper is to obtain the holonomies of $F^{s}_{Y}$ and $F^{u}_{Y}$ from the holonomies of $F^{s}_{X}$ and $F^{u}_{X}$ by using Proposition 4.2. In §4.5 we will first describe the change of holonomies for the unstable holonomies in the $C_{+,+}$ quadrants and then we will explain how to adapt the previous statement in all the other quadrants.

Before doing that, we need to explain which holonomies of $F^{u}_{Y}$ and $F^{u}_{X}$ will be compared. More precisely, consider a point $p_{X}\in {\mathcal P}_{X}$ , a point $q_{X}\in F^{u}_{+}(p_{X})$ and the unstable holonomy $h^{u}_{X,p_{X},q_{X}}$ from $F^{s}_{X,+}(p_{X})$ to $F^{s}_{X,+}(q_{X})$ . We want to describe the effect of the surgery on this holonomy and to compare the new holonomy with $h^{u}_{X,p_{X},q_{X}}$ .

Consider the path $\sigma _{X}$ obtained by the concatenation of:

• • the half stable leaf $F^{s}_{X,+}(p_{X})$ (with the negative orientation);

• • the unstable segment $[p_{X},q_{X}]^{u}$ ;

• • the half stable leaf $F^{s}_{X,+}(q_{X})$ .

We fix a parametrization of $\sigma _{X}$ so that the path $\sigma _{X}$ becomes a map $\sigma _{X}\colon {\mathbb R}\to {\mathcal P}_{X}$ .

4.4.1 The easy case: no point of $\tilde \Gamma $ on $\sigma _{X}$

Assume first that $\sigma _{X}$ is disjoint from $\tilde \Gamma _{X}$ . Consider a lift $p_{\Gamma }\in {\mathcal P}_{\Gamma }$ of $p_{X}$ and let $p_{Y}\in {\mathcal P}_{Y}$ be the projection of $p_{\Gamma }$ .

Now $\sigma _{X}$ has a well-defined lift $\sigma _{\Gamma }$ on ${\mathcal P}_{\Gamma }$ through $p_{\Gamma }$ . Consider $\sigma _{Y}$ the projection of $\sigma _{\Gamma }$ . In other words, we have

$$ \begin{align*}\sigma_{Y}=\Pi_{Y}(\Pi^{-1}_{X}(\sigma_{X})),\end{align*} $$

and $\sigma _{Y}(t)=\Pi _{Y}(\Pi ^{-1}_{X}(\sigma _{X}))$ will be called the corresponding point of $\sigma _{X}(t)$ in ${\mathcal P}_{Y}$ .

Thus $q_{Y}$ is the corresponding point of $q_{X}$ in ${\mathcal P}_{Y}$ and belongs to $F^{u}_{+}(p_{Y})$ . So the unstable holonomy $h^{u}_{Y,p_{Y},q_{Y}}$ from $F^{s}_{Y,+}(p_{Y})$ to $F^{s}_{Y,+}(q_{Y})$ is well defined.

As every point in $F^{s}_{+}(p_{X})$ (respectively, in $F^{s}_{+}(q_{X})$ ) has a corresponding point in $F^{s}_{+}(p_{Y})$ (respectively, in $F^{s}_{+}(q_{Y})$ ), it makes sense to compare $h^{u}_{X,p_{X},q_{X}}$ with $h^{u}_{Y,p_{Y},q_{Y}}$ .

4.4.2 The general case

In the next section we will need to compare holonomies of X and Y corresponding to stable leaves that intersect $\tilde \Gamma _{X}$ and $\tilde \Gamma _{Y}$ , in other words, we will consider the case where $\sigma _{X}$ is not disjoint from $\tilde {\Gamma }_{X}$ . In this case, $\sigma _{X}$ no longer lifts on ${\mathcal P}_{\Gamma }$ . We have seen in §4.2 that one may associate different paths $\gamma _{Y}$ in ${\mathcal P}_{Y}$ to a path $\gamma $ in ${\mathcal P}_{X}$ , depending, roughly speaking, on whether we choose to move at the right or at the left of x for every x in $\gamma _{X}\cap \tilde \Gamma _{X}$ .

The aim of this subsection is to fix our choices for the segment $\sigma _{X}$ .

Consider a point $p_{X}\in {\mathcal P}_{X}$ and $p_{Y}\in {\mathcal P}_{Y}$ , which are obtained in one of the following ways:

• • either as the projections of a same point $p_{\Gamma } \in {\mathcal P}_{\Gamma }$ , which means, in particular, that $p_{X}\notin \tilde \Gamma _{X}$ ;

• • or, if $p_{X}\in \tilde \Gamma _{X}$ , we consider a small rectangle $R_{X,+,+}$ admitting $p_{X}$ as its lower left corner and such that $R_{X,+,+} \cap \tilde {\Gamma }_{X}=\{p_{X}\}$ . We lift $R_{X,+,+}\setminus \{p_{X}\}$ on ${\mathcal P}_{\Gamma }$ and we project this lift on ${\mathcal P}_{Y}$ . One gets a rectangle $R_{Y,+,+}$ punctured at its lower left corner, which is denoted by $p_{Y}\in \tilde \Gamma _{Y}$ .

Given a point $q_{X}$ in $F^{u}_{X,+}(p_{X})$ , we previously defined a path $\sigma _{X}$ obtained by the concatenation of $\sigma ^{1}_{X}=F^{s}_{X,+}(p_{X})$ (with negative orientation), $\sigma ^{2}_{X}=[p_{X},q_{X}]^{u}$ and $\sigma ^{3}_{X}=F^{s}_{X,+}(q_{X})$ .

The point $q_{Y}\in {\mathcal P}_{Y}$ corresponding to $q_{X}$ will be the end point of the path $\sigma ^{2}_{Y,+}$ , defined in §4.2 and whose origin is $p_{Y}$ .

We want to compare the unstable holonomy $h^{u}_{X,p_{X},q_{X}}$ with the unstable holonomy $h^{u}_{Y,p_{Y},q_{Y}}$ for Y. In order to do that, we consider the path $\sigma _{Y}$ obtained by the concatenation of three paths (see Figure 7):

• • the half stable leaf $\sigma ^{1}_{Y,+}$ (which corresponds to $F^{s}_{Y,+}(p_{Y})$ , negatively oriented);

• • the unstable segment $\sigma ^{2}_{Y,+}$ (joining $p_{Y}$ to $q_{Y}$ );

• • the half stable leaf $\sigma ^{3}_{Y,-}$ (which corresponds to $F^{s}_{Y,+}(q_{Y})$ , positively oriented)

Figure 7 The dotted curves correspond to the approximations used in order to construct $\sigma _{Y}$ .

The construction of the paths $\sigma ^{i}_{Y,\pm }$ (see §4.2) induces a homeomorphism from $\sigma ^{i}_{X}$ to $\sigma ^{i}_{Y}$ , mapping $\sigma ^{i}_{X}(t)$ on $\sigma ^{i}_{Y}(t)$ . By gluing these homeomorphisms together, we get a homeomorphism between $\sigma _{X}$ and $\sigma _{Y}$ , mapping $\sigma _{X}(t)$ on $\sigma _{Y}(t)$ .

For any point $z_{X}=\sigma _{X}(t)$ , we define its corresponding point as $z_{Y}:=\sigma _{Y}(t)$ .

Remark 4.3. Our choice to define $\sigma _{Y}$ as the concatenation of the paths $\sigma ^{1}_{Y,+} \sigma ^{2}_{Y,+}$ and $\sigma ^{3}_{Y,-}$ may look arbitrary. According to the previous definition, $\sigma _{Y}$ corresponds to the projection on ${\mathcal P}_{Y}$ of the lifts of a sequence of (continuous) paths $\sigma _{X,n}$ disjoint from $\tilde \Gamma _{X}$ , converging to $\sigma _{X}$ and approaching $F^{s}_{X,+}(p_{X})$ from above, $[p_{X},q_{X}]^{u}$ from the right and $F^{s}_{X,+}(q_{X})$ from above. In particular, the paths $\sigma _{X,n}$ are contained in $C_{+,+}(p_{X})$ and intersect $F^{s}_{X,+}(q_{X})$ .

In the terms of the holonomy $h^{u}_{Y,p_{Y},q_{Y}}$ , this means that we will suppose that the segments $[y,h^{u}_{Y,p_{Y},q_{Y}}(y)]^{u}$ do not ‘cross’ $F^{s}_{Y,+}(p_{Y})$ , but they do ‘cross’ $F^{s}_{Y,+}(q_{Y})$ . (Another choice of $\sigma ^{i}_{Y}$ would not change the definition of the holonomy $h^{u}_{Y,p_{Y},q_{Y}}$ , but would change the parametrization of the path $\sigma _{Y}$ , thus interfering in the comparison of holonomies.)

This particular choice is convenient for composing holonomies.

4.5 Comparison of the holonomies in the quadrants: the formula

We are now ready to compare the holonomies $h^{u}_{X,p_{X},q_{X}}$ and $h^{u}_{Y,p_{Y},q_{Y}}$ .

Theorem 13. With the notation above, let $x_{Y}\in F^{s}_{Y,+} (p_{Y})$ . Then

$$ \begin{align*}h^{u}_{Y,p_{Y},q_{Y}}(x_{Y})=y_{Y}\end{align*} $$

if and only if there exist $\ell \in {\mathbb N}$ and two finite sequences $t_{i}\in {\mathbb R}$ and $x_{i}\in {\mathcal P}_{X}$ with $i\in \{0,\ldots , \ell \}$ such that the following statements hold.

1. (1) $x_{0}=x_{X}$ and $x_{l}=y_{X}$ .

2. (2) $\sigma _{X}(t_{0})=p_{X}$ , $\sigma _{X}(t_{\ell })=q_{X}$ .

3. (3) $t_{i}<t_{i+1}$ for $i\in \{0,\ldots , \ell -2\}$ and $t_{\ell -1} \leq t_{\ell }$ , therefore $\sigma _{X}(t_{i})\in [p_{X},q_{X}]^{u}$ . We denote $q_{X,i}=\sigma _{X}(t_{i})$ .

4. (4) For $i\in \{1,\ldots ,\ell -1\}$ there exists $\mu _{i}\in \tilde \Gamma _{X}$ (see Figure 8) such that the point $q_{X,i}$ belongs to $F^{s}_{X,-}(\mu _{i})$ and the point $x_{i}$ belongs to $F^{s}_{X,+}(\mu _{i})$ . We denote by $k_{i}$ the corresponding characteristic number of the surgery and we take $k_{0}=0$ .

   

   Figure 8 In this figure we performed negative surgeries along the red periodic points ( ) and positive along the blue ones ( ). Every time we hit a stable manifold of either a blue or red point the holonomy is respectfully contracted or expanded. Colour available online.

5. (5) $\{x_{1}\}=F_{X}^{u}(x_{0})\cap F_{X}^{s}(q_{X,1})$ and $\{x_{i+1}\}=F_{X}^{u}(P^{k_{i}}_{\mu _{i}}(x_{i}))\cap F_{X}^{s}(q_{X,i+1})$ (where $P_{\mu _{i}}$ is the first return map of X associated to $\mu _{i}$ see Lemma 3.2) for $i \in \{1,\ldots ,\ell -1\}$ .

6. (6) Let $R_{i}$ for $i\in \{0,\ldots ,\ell -1\}$ be the rectangle ( $R_{\ell -1}$ can be degenerated) bounded by the segments $[q_{X,i},q_{X,i+1}]^{u}$ , $[q_{X,i+1}, x_{i+1}]^{s}$ , $[q_{X,i}, P^{k_{i}}_{\mu _{i}}(x_{i})]^{s}$ and $[P^{k_{i}}_{\mu _{i}}(x_{i}),x_{i+1}]^{u}$ . Then the interior of $R_{i}$ is disjoint from $\tilde \Gamma _{X}$ .

Proof. If $q_{X}$ does not belong to the negative stable manifold of a point $\mu $ on which we have performed surgery, the above theorem is obtained by a simple induction argument using Proposition 4.2.

Otherwise, we can use a simple induction argument to calculate the holonomy from $F^{s}_{X,+}(p_{X})$ to $F^{s}_{X,+}(q^{-}_{X})$ , where $q^{-}_{X} \in [p_{X},q_{X}]^{u}$ and satisfies the hypothesis of the previous case. $q^{-}_{X}$ can be taken as close as we want to $q_{X}$ . By Proposition 4.2 and because of our choice of $\sigma _{X}$ and $\sigma _{Y}$ , we have that changing the surgery on $\mu $ would change the parametrization of the path $\sigma ^{\prime \prime }_{Y,-}$ . Therefore, in order to compute the holonomy from $F^{s}_{X,+}(q^{-}_{X})$ to $F^{s}_{X,+}(q_{X})$ we must apply Proposition 4.2 for two rectangles $R^{-}$ and $R^{+}$ , where $R^{+}$ is degenerated.

Let us make some remarks about the previous theorem.

Remark 4.4. In the above theorem, $\sigma _{X}$ and $\sigma _{Y}$ play the roles of local coordinates on each bifoliated plane. Changing the definition of the above coordinates would naturally change the statement of the theorem and therefore the computation of the holonomy.

Remark 4.5.

• • The same statement holds for the holonomies in the $C_{-,-}$ quadrant by changing $F^{s}_{X,+}$ and $F^{u}_{X,+}$ to $F^{s}_{X_{-}}$ and $F^{u}_{X,-}$ . In fact, it is enough to apply Theorem 13 after changing the orientation of both foliations $F^{s}_{X}$ and $F^{u}_{X}$ . This change preserves the orientation of the manifold and hence preserves the characteristic numbers $k_{i}$ of the surgery.

• • An analogous statement holds in the $C_{+,-} C_{-,+}$ quadrants, but one needs to change the sign of the characteristic numbers, therefore to change $k_{i}$ to $-k_{i}$ . For that, we apply Theorem 13 after changing only one of the two orientations of $F^{s}_{X}$ and $F^{u}_{X}$ , thus changing the orientation of M and eventually the orientation of the meridian. For this new orientation, the characteristic number of the surgery changes sign.

Remark 4.6. According to §3.6.1, the statement of Theorem 13 can be easily adapted for the case where $\Gamma =\{\gamma _{1},\ldots ,\gamma _{k}\}$ contains orbits with negative eigenvalues.

More specifically, if the point $\mu _{i}\in \tilde \Gamma _{X}$ corresponds to an orbit $\gamma \in \Gamma $ with negative eigenvalues, then $k_{i}$ should be taken equal to $4$ times the characteristic number $n(\gamma )$ of the surgery performed along $\gamma $ . That is because the surgery along $\gamma $ corresponds, on the orientation cover, to a surgery with characteristic number $2n(\gamma )$ along the lifted orbit $\hat \gamma $ , whose first return map is the square of the first return map of $\gamma $ .

4.6 The special case where X is a suspension: calculating the holonomies as a dynamical game

In this section we assume that X is the suspension flow of a hyperbolic Anosov diffeomorphism $f_{A}$ , where $A\in SL(2,{\mathbb Z})$ is a hyperbolic matrix with positive eigenvalues $0<\lambda ^{-1}<1<\lambda $ . We will explain how our arguments can be adapted for the case of matrices in $SL(2,{\mathbb Z})$ with negative eigenvalues in §4.6.4.

In this particular case, the bifoliated plane is trivial, so the holonomies are also trivial in ${\mathcal P}_{X}$ and the first return maps are simple to understand. This will simplify significantly the statement of Theorem 13.

We perform a linear change of coordinates on ${\mathcal P}_{X}={\mathbb R}^{2}$ so that $F^{s}_{X}$ is the horizontal foliation and $F^{u}_{X}$ is the vertical foliation. In these coordinates, A is the linear map

$$ \begin{align*}{\mathcal A}=\left(\begin{array}{@{}cc@{}} \lambda^{-1}&0\\ 0&\lambda \end{array}\right)\end{align*} $$

We now consider:

• • two finite sets ${\mathcal X}$ and ${\mathcal Y}$ of ${\mathbb T}^{2}$ which are disjoint and $f_{A}$ -invariant. Every point x in ${\mathcal X}\cup {\mathcal Y}$ is periodic and we denote by $\tau (x)$ its period. Notice that $\tau $ is invariant by $f_{A}$ .

• • two functions $m\colon {\mathcal X}\to {\mathbb N}$ and $n\colon {\mathcal Y}\to {\mathbb N}$ which are $f_{A}$ -invariant.

By a convenient abuse of language, we will still denote by ${\mathcal X}$ and ${\mathcal Y}$ the periodic orbits of the vector field X. In this way, the functions m and n become integer functions on this finite set of orbits of X.

We denote by $\tilde {\mathcal X}$ and $\tilde {\mathcal Y}$ the lifts of ${\mathcal X}$ and ${\mathcal Y}$ on ${\mathcal P}_{X}$ , which is canonically identified with the universal cover of the torus ${\mathbb T}^{2}$ . We still denote by $\tau $ , m and n the lifts of the previous functions.

In the previous section we defined the first return map $P_{ x}$ associated to a point $x\in {\mathcal P}_{X}$ corresponding to a periodic orbit of X. In our setting, the first return map associated to a point $ x\in \tilde {\mathcal X}\cup \tilde {\mathcal Y}$ is the affine map having $ x$ as its unique fixed point and ${\mathcal A}^{\tau (x)}$ as its linear part:

$$ \begin{align*}P_{x}= p\mapsto {\mathcal A}^{\tau(x)}(p-x) + x.\end{align*} $$

We denote by Y the vector field obtained from X by performing surgeries with characteristic numbers m on the orbits in ${\mathcal X}$ and $-n$ on the orbits in ${\mathcal Y}$ .

We denote

$$ \begin{align*}\mu= m\cdot \tau \quad\mbox{and}\quad \nu=n\cdot \tau.\end{align*} $$

The aim of this section is to express Theorem 13 in this particular setting.

Consider a point $p=p_{X}=(p^{s},p^{u})\in {\mathbb R}^{2}$ . We want to describe the holonomies of $F^{s}_{Y}$ and $F^{u}_{Y}$ in the quadrants $C_{\pm ,\pm }(p_{Y})$ , where $p_{Y}$ is the projection on ${\mathcal P}_{Y}$ of a lift of $p_{X}$ on the universal cover of ${\mathcal P}_{X}\setminus (\tilde {\mathcal X}\cup \tilde {\mathcal Y})$ . Let us start from the $C_{+,+}$ quadrant, in order to avoid useless formalism.

4.6.1 In the $C_{+,+}$ quadrants

Consider $r>0$ , $t_{0}>0$ , a point $q=(p^{s}, p^{u}+r)$ in the positive unstable manifold of p, a point $z_{0}=(p^{s}+t_{0}, p^{u})$ in the positive stable manifold of p, and their corresponding points $p_{Y},z_{0,Y}$ in ${\mathcal P}_{Y}$ . One would like to know if the holonomy $h^{u}_{p,q}$ of $F^{u}_{Y}$ from the positive stable manifold of $p_{Y}$ to the positive stable manifold of $q_{Y}$ is defined on $z_{0,Y}$ , and if this is the case, what its value is.

In order to answer the previous question, one considers the set of points $z_{s}=(p^{s}+t_{0}, p^{u}+s)$ in ${\mathcal P}_{X}$ , with $0<s < s_{1} \leq r$ , where $s_{1}$ is the smallest positive real for which there exists a point $\gamma _{1}=(p^{s}+u_{1},p^{u}+s_{1})\in \tilde {\mathcal X}\cup \tilde {\mathcal Y}$ , with $0<u_{1}<t_{0}$ . If such an $s_{1}$ does not exist, then the holonomy from $W^{s}_{+}(p)$ to $W^{s}_{+}(q)$ is defined on $(p^{s}+t_{0}, p^{u})$ and its value is $(p^{s}+t_{0}, p^{u}+r)$

If such an $s_{1}$ exists (see Figure 9), then one defines $z_{s}=(p^{s}+t_{1}, p^{u}+s)$ , with $s\in [s_{1},s_{2})$ , where

• • $t_{1}= u_{1}+\lambda ^{-\mu (\gamma _{1})}(t_{0}-u_{1})$ if $\gamma _{1}\in \tilde {\mathcal X}$ ,

• • $t_{1}= u_{1}+\lambda ^{\nu (\gamma _{1})}(t_{0}-u_{1})$ if $\gamma _{1}\in \tilde {\mathcal Y}$ , and

• • $s_{2}$ is the smallest positive number in $(s_{1},r]$ such that $z_{t}$ crosses the positive stable manifold of a point $\gamma _{2}=(p^{s}+u_{2},p^{u}+s_{2})\in \tilde {\mathcal X}\cup \tilde {\mathcal Y}$ , with $0<u_{2}<t_{1}$ .

Figure 9 In this figure the periodic points on which we performed positive surgery are represented by blue ( ) and the others by red ( ). Colour available online.

Analogously, if such an $s_{2}$ does not exist then the holonomy from $W^{s}_{+}(p)$ to $W^{s}_{+}(q)$ is defined on $(p^{s}+t_{0}, p^{u})$ and its value is $(p^{s}+t_{1}, p^{u}+r)$ . If $s_{2}$ exists, then one defines $z_{s}=(p^{s}+t_{2}, p^{u}+s)$ , $s\in [s_{2},s_{3})$ , where

• • $t_{2}= u_{2}+\lambda ^{-\mu (\gamma _{2})}(t_{1}-u_{2})$ if $\gamma _{2}\in \tilde {\mathcal X}$ ,

• • $t_{2}= u_{2}+\lambda ^{\nu (\gamma _{2})}(t_{1}-u_{2})$ if $\gamma _{2}\in \tilde {\mathcal Y}$ , and

• • $s_{3}$ is the smallest positive number in $(s_{2},r]$ such that $z_{t}$ crosses the positive stable manifold of a point $\gamma _{3}=(p^{s}+u_{3},p^{u}+s_{3})\in \tilde {\mathcal X}\cup \tilde {\mathcal Y}$ , with $0<u_{3}<t_{2}$ .

We define by induction the sequences $t_{i}$ , $s_{i+1}$ , $u_{i+1}$ , $\gamma _{i+1}$ : $z_{s}=(p^{s}+t_{i}, p^{u}+s)$ , $s\in [s_{i},s_{i+1})$ , where

• • $t_{i}= u_{i}+\lambda ^{-\mu (\gamma _{i})}(u_{i}-t_{i-1})$ if $\gamma _{i}\in \tilde {\mathcal X}$ ,

• • $t_{i}= u_{i}+\lambda ^{\nu (\gamma _{i})}(u_{i}-t_{i-1})$ if $\gamma _{i}\in \tilde {\mathcal Y}$ , and

• • $s_{i+1}$ is the smallest positive number in $(s_{i},r]$ such that $z_{t}$ crosses the positive stable manifold of a point $\gamma _{i+1}=(p^{s}+u_{i+1},p^{u}+s_{i+1})\in \tilde {\mathcal X}\cup \tilde {\mathcal Y}$ , with $0<u_{i+1}<t_{i}$ .

Now,

• • either this process is repeated infinitely many times, in which case the holonomy $h^{u}_{p,q}$ is not defined at the point $z_{0}$ ,

• • or the process ends when, for some $i\in \mathbb {N}$ , $s_{i}$ is not defined, in which case $h^{u}_{p,q}$ is defined at the point $z_{0}$ and

  $$ \begin{align*}h^{u}_{p,q}(z_{0})= z_{r}.\end{align*} $$

In this game, one sees that:

• • the points in $\tilde {{\mathcal X}}$ induce a contraction of the horizontal coordinate of $z_{s}$ , increasing the chances of the holonomy being defined on $z_{0}$ ;

• • a contrario the points in $\tilde {{\mathcal Y}}$ induce an expansion of the horizontal coordinate of $z_{s}$ , making it in this way more likely to meet the positive stable manifold of new points in $\tilde {\mathcal X}\cup \tilde {\mathcal Y}$ . If the new points are in $\tilde {{\mathcal Y}}$ , the expansion continues. This explains why, after surgeries, the quadrant $C_{+,+}(p)$ may be no more complete for Y. This is what happens if $\tilde {{\mathcal X}}$ is empty, which was already shown in [Fe1].

When playing the previous game, an important tool emerges: if two successive points $\gamma _{i}$ and $\gamma _{i+1}$ both belong to $\tilde {\mathcal X}$ (respectively, $\tilde {\mathcal Y}$ ), then there is a rectangle admitting $\gamma _{i}$ and $\gamma _{i+1}$ as corners, which is disjoint from $\tilde {\mathcal Y}$ (respectively, from $\tilde {\mathcal X}$ ). This rectangle will be the main object of §7. The existence or not of such rectangles is what determines the different cases that we consider in our study.

4.6.2 In the $C_{-,-}$ quadrants

The game in the $C_{-,-}$ quadrants is identical: crossing the negative stable manifold of a point in $\tilde {{\mathcal Y}}$ (respectively, $\tilde {{\mathcal X}}$ ) induces an expansion (respectively, contraction).

4.6.3 In the $C_{-,+}$ and $C_{+,-}$ quadrants

In the $C_{+,-}$ and $C_{-,+}$ quadrants, the description of the game is similar, but the roles of $\tilde {{\mathcal X}}$ and $\tilde {{\mathcal Y}}$ are interchanged (the unique difference in the formulas is the sign before $\mu $ and $\nu $ ):

• • $t_{i}= u_{i}+\lambda ^{+\mu (\gamma _{i})}(u_{i}-t_{i-1})$ if $\gamma _{i}\in \tilde {\mathcal X}$ ,

• • $t_{i}= u_{i}+\lambda ^{-\nu (\gamma _{i})}(u_{i}-t_{i-1})$ if $\gamma _{i}\in \tilde {\mathcal Y}$ .

Thus in these quadrants crossing the stable (positive or negative, according to the quadrant) separatrix of a point in $\tilde {{\mathcal Y}}$ induces a contraction and crossing the separatrix of a point in $\tilde {{\mathcal X}}$ induces an expansion.

4.6.4 Matrices with negative eigenvalues

According to §3.6.1 and Remark 4.6, the dynamical game can be adapted in the case of negative eigenvalues as follows: when playing the game, if the point $\gamma _{i}$ corresponds to a periodic orbit in ${\mathcal X}\cup {\mathcal Y}$ with negative eigenvalues, then we should replace $\mu (\gamma _{i})$ and $\nu (\gamma _{i})$ by $4\mu (\gamma _{i})$ and $4\nu (\gamma _{i})$ , respectively.

5 Surgeries on the geodesic flow and ${\mathbb R}$ -covered Anosov flows

The main goal of this section is to prove Theorem 1: surgeries along a set of periodic orbits associated to disjoint simple closed geodesics do not change the bifoliated plane.

We start by formulating a general criterion for preserving the ${\mathbb R}$ -covered character of Anosov flows after surgeries.

5.1 ${\mathbb R}$ -covered Anosov flows

We recall that for any finite set of periodic orbits $\Gamma $ , ${{\mathcal S}}urg(X, \Gamma )$ denotes the set of Anosov flows obtained by X by performing surgeries on $\Gamma $ up to orbital equivalence. In this section, X is either a suspension or a positively twisted Anosov flow. In other words, the bifoliated plane $({\mathcal P}_{X}, F^{s}_{X},F^{u}_{X})$ is either trivial or conjugated to the restriction of the trivial (horizontal/vertical) foliations of ${\mathbb R}^{2}$ to the strip $\{(x,y)\in {\mathbb R}^{2}, |x-y|<1\}$ .

According to Corollary 3.2, our hypothesis is equivalent to the following property: for any $x\in {\mathcal P}_{X}$ the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ have the complete intersection property (in other words, they are complete).

For every $x\in {\mathcal P}_{X}$ , let us denote

$$ \begin{align*}\Delta_{+}(x)=\{y\in {\mathcal P}_{X}, F^{s}_{+}(x)\cap F^{u}_{-}(y)\neq \emptyset \mbox{ and }F^{u}_{+}(x)\cap F^{s}_{-}(y)\neq \emptyset\},\end{align*} $$

$$ \begin{align*}\Delta_{-}(x)=\{y\in {\mathcal P}_{X}, F^{s}_{-}(x)\cap F^{u}_{+}(y)\neq \emptyset \mbox{ and }F^{u}_{-}(x)\cap F^{s}_{+}(y)\neq \emptyset\}.\end{align*} $$

These sets are included respectively in $C_{+,+}(x)$ and $C_{-,-}(x)$ . Our hypothesis is equivalent to the fact that for any $x\in {\mathcal P}_{X}$ , $\Delta _{+}(x)$ and $\Delta _{-}(x)$ are conjugated to the trivially bifoliated plane.

The announced criterion is stated in the following corollary.

Corollary 5.1. Let X be an Anosov flow which is ${\mathbb R}$ -covered positively twisted. Let $\Gamma $ be a finite set of periodic orbits of X Assume that for all $x\in \tilde \Gamma _{X}$ corresponding to $\gamma \in \Gamma $ ,

$$ \begin{align*} \Delta_{+}(x)\cap \tilde{\Gamma}_{X}=\emptyset=\Delta_{-}(x)\cap \tilde \Gamma_{X}.\end{align*} $$

Then every $Y \in {{\mathcal S}}urg(X,\Gamma )$ is ${\mathbb R}$ -covered positively twisted.

Corollary 5.1 will be obtained as consequence of the following two propositions.

Proposition 5.1. Let X be an Anosov flow which is either a suspension or ${\mathbb R}$ -covered positively twisted. Let $\Gamma $ be a finite set of periodic orbits of X and $Y \in {{\mathcal S}}urg(X,\Gamma )$ . Assume that for every $x\in \tilde \Gamma _{Y}$ the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ are complete. Then Y is either a suspension or is ${\mathbb R}$ -covered positively twisted.

In other words, the completeness of the $C_{+,+}$ and $C_{-,-}$ quadrants at the points where we performed the surgery guarantees the completeness of every $C_{+,+}$ and $C_{-,-}$ quadrant.

Proposition 5.2. Let X be an Anosov flow which is either a suspension or ${\mathbb R}$ -covered positively twisted. Let $\Gamma $ be a finite set of periodic orbits of X and $Y \in {{\mathcal S}}urg(X,\Gamma )$ . Assume that there is $x\in \tilde \Gamma _{X}$ corresponding to $\gamma \in \Gamma $ such that

$$ \begin{align*} \Delta_{+}(x)\cap \tilde{\Gamma}_{X}=\emptyset.\end{align*} $$

Then for any $y\in \tilde {\Gamma }_{Y}$ corresponding to $\gamma $ , we have that $C_{+,+}(y)$ is complete. The same statement holds if we change $\Delta _{+}(x)$ to $\Delta _{-}(x)$ and $C_{+,+}(y)$ to $C_{-,-}(y)$ .

Remark 5.1. The above hypothesis $ \Delta _{+}(x)\cap \tilde {\Gamma }_{X}=\emptyset $ remains valid for all z in the $\pi _{1}(M)$ -orbit of x. Indeed, for any point z in the orbit of x there is an element of $\pi _{1}(M)$ mapping $\Delta _{+}(x)$ onto $\Delta _{+}(z)$ (even if the eigenvalues of $\gamma $ are negative).

Proof of Proposition 5.2

This is a straightforward consequence of Theorem 13 applied for $\ell =1$ : the positive unstable leaves $F^{u}_{X,+}(z)$ with $z\in F^{s}_{X,+}(x)$ do not meet any positive stable separatrix of an element in $\tilde \Gamma _{X}$ . Therefore, the holonomies in $\Delta _{+}(x)$ are not affected at all by the surgeries on $\Gamma $ .

Corollary 5.1 is a straightforward consequence of Propositions 5.1 and 5.2. We therefore only need to prove Proposition 5.1.

Proof of Proposition 5.1

Assume, by contradiction, that there is $x_{Y}\in {\mathcal P}_{Y}$ such that the quadrant $C_{+,+}(x_{Y})$ (or $C_{-,-}(x_{Y})$ ) does not have the complete intersection property. In other words, there is $z_{Y}\in F^{u}_{Y,+}(x_{Y})$ such that the holonomy $h^{u}_{Y,x_{Y},z_{Y}}$ is not defined on the whole of $F^{s}_{Y,+}(x_{Y})$ . However, by transversality, the holonomy is defined on an open interval containing $x_{Y}$ , so there exists a first point $y_{Y}$ on which the holonomy is not defined.

Consider the triple of corresponding points $x_{X}$ , $z_{X}\in F^{u}_{X,+}(x)$ , $y_{X}\in F^{s}_{X,+}(x_{X})$ .

As the holonomy is not defined at $y_{Y}$ , Theorem 13 implies that $F^{u}_{X,+}(y_{X})$ intersects the positive stable separatrix of a point in $\tilde \Gamma _{X}$ between $F^{u}_{X,+}(x_{X})$ and $F^{u}_{X,+}(y_{X})$ (see Figure 10). Let $\tilde \gamma _{X}$ be the first such point. There exists a rectangle R, whose interior is disjoint from $\tilde {\Gamma }_{X}$ and whose boundary consists of $[x_{X},y_{X}]^{s}$ , a segment of $F^{u}_{X,+}(x_{X})$ , a segment of $F^{u}_{X,+}(y_{X})$ and a segment of $F^{s}_{X}(\tilde\gamma _{X})$ containing $\tilde\gamma _{X}$ . Hence, there is a point $y_{0}$ in $F^{u}_{X}(\tilde \gamma _{X})\cap F^{s}_{X,+}(x_{X})$ belonging to $(x_{X},y_{X})^{s}$ .

Figure 10 $F_{X,+}(y_x)$ will eventually enter the $(+,+) $ -quadrant of a point in $\tilde{\Gamma}_X$ . Colour available online.

This implies that the holonomy map $h^{u}_{Y,x_{Y},z_{Y}}$ is defined on $y_{0,Y}$ , hence $F^{u}_{Y,+} (\tilde \gamma _{Y})$ cuts $F^{s}_{Y,+}(z_{Y})$ .

In other words, both $F^{u}_{Y,+}(y_{Y})$ and $F^{s}_{Y,+}(z_{Y})$ eventually enter the quadrant $C_{+,+}(\tilde \gamma _{Y})$ . By assumption, $C_{+,+}(\tilde \gamma _{Y})$ is complete, so $F^{u}_{Y,+}(y_{Y})\cap F^{s}_{Y,+}(z_{Y})\neq \emptyset $ which contradicts our initial hypothesis.

5.2 The geodesic flow

Theorem 1 is now a straightforward consequence of the following proposition.

Proposition 5.3. Let S be a hyperbolic surface. Let $\Gamma =\{\gamma _{1}^{+},\gamma _{1}^{-},\ldots ,\gamma _{k}^{+}, \gamma _{k}^{-}\}$ be orbits of the geodesic flow X corresponding to closed simple disjoint geodesics $(c_{1},\ldots , c_{k})$ . Then,for any $\tilde \gamma $ in $\tilde \Gamma _{X}$ ,

$$ \begin{align*}\Delta_{+}(\tilde \gamma)\cap \tilde{\Gamma}_{X}=\emptyset=\Delta_{-}(\tilde \gamma)\cap \tilde \Gamma_{X}.\end{align*} $$

Proposition 5.3 is itself a straightforward consequence of the next lemma.

Lemma 5.1. Consider $x\in {\mathcal P}_{X}$ and the corresponding geodesic $\gamma _{x}$ in the Poincaré disk ${\mathbb D}$ . Then $\Delta _{+}(x)$ is identified with the set of geodesics cutting transversely and positively $\gamma _{x}$ .

Proof. The geodesics $\sigma \subset {\mathbb D}$ positively crossing a given geodesic $\gamma \subset {\mathbb D}$ are in one-to-one correspondence with the set of pairs of points $(\alpha (\sigma ),\omega (\sigma ))\in \partial {\mathbb D}$ , which belong to different connected components of ${\mathbb D}\setminus \{ \alpha (\gamma ),\omega (\gamma )\}$ . Now $\sigma $ is the unique intersection point between the stable manifold of the geodesic associated to $(\alpha (\gamma ), \omega (\sigma ))\in F^{u}(\gamma )$ and the unstable manifold of the geodesic associated to $(\alpha (\sigma ), \omega (\gamma ))\in F^{s}(\gamma )$ .

6 Surgeries preserving the branching structure of a non- ${\mathbb R}$ -covered Anosov flow

The aim of this section is to make an observation, which is almost clear after reading [Fe2]. (Fenley told us that, at the time he wrote [Fe2] he was aware of this result, but did not publish it. We thought that the present paper would be a good place to do so.) The results of this section generalize Theorems 2 and 3.

Given an Anosov vector field X, Fenley proved in [Fe2] that the following statements hold.

1. (1) The leaves of $F^{s}_{X}$ which are not separated correspond to finitely many periodic orbits of X. Let us denote this set of orbits ${{\mathcal S}}^{s}(X)= {{\mathcal S}}^{s}_{+}(X)\cup {{\mathcal S}}^{s}_{-}(X)$ , where ${{\mathcal S}}^{s}_{+}(X)$ and ${{\mathcal S}}^{s}_{-}(X)$ correspond to the leaves which are not separated from above and from below, respectively. The sets ${{\mathcal S}}^{s}_{+}(X),{{\mathcal S}}^{s}_{-}(X)$ are not necessarily disjoint.

2. (2) Similarly, the leaves of $F^{u}_{X}$ which are not separated correspond to a finite set of periodic orbits of X denoted by

   $$ \begin{align*}{{\mathcal S}}^{u}(X)= {{\mathcal S}}^{u}_{+}(X)\cup{{\mathcal S}}^{u}_{-}(X).\end{align*} $$

3. (3) The set of stable leaves in ${\mathcal P}_{X}$ , which are not separated from below from a given leaf $L^{s}_{0}$ , are ordered as an interval of ${\mathbb Z}$ , so let us denote them $\{L_{i}, i\in I\subset {\mathbb Z}\}$ . For each pair $L_{i},L_{i+1}$ of successive non-separated leaves from below:

   • • there is $\gamma $ in $\pi _{1}(M)$ fixing both leaves $L_{1}$ and $L_{2}$ . Each of those leaves contains a fixed point $x_{i}$ for the action of $\gamma $ on ${\mathcal P}_{X}$ .

   • • there is a proper embedding $\phi $ of $[-1,1]^{2}\setminus \{(-1,-1),(0,1),(1,-1)\}$ in ${\mathcal P}_{X}$ conjugating the trivial foliations with $F^{s}_{X}$ and $F^{u}_{X}$ and whose image is uniquely associated to the pair $(L_{1},L_{2})$ .

   • • The image of an orientation-preserving embedding of the trivially bifoliated $[0,1]^{2}\setminus \{(0,0),(1,1)\}$ that cannot be extended to $\{(0,0),(1,1)\}$ is called a positive lozenge. Similarly, the image of an orientation-preserving embedding of the trivially bifoliated $[0,1]^{2}\setminus \{(0,1),(1,0)\}$ that cannot be extended to $\{(0,1),(1,0)\}$ is called a negative lozenge. The points $\{(0,1),(1,0)\}$ (respectively, $ \{(0,0),(1,1)\}$ ) in the first (respectively, second) case will be called corner points of the lozenge.

   • • Following the terminology in [Fe2], the image of $\phi $ is a pair of adjacent lozenges, one of which is positive and the other negative (see Figure 11). The points $(-1,1),(1,1)$ correspond to $x_{1},x_{2}$ and the point $(0,-1)$ , whose positive unstable leaf ends at the missing point $(0,1)$ is called the pivot associated to $L_{1}$ , $L_{2}$ and is unique, hence also a fixed point of $\gamma $ . The set of pivots associated to non-separated stable leaves from below will be denoted by $Piv^{s}_{-}(X)$ .

     

     Figure 11 An example of a pivot point in $Piv^{s}_{-}(X)$ .

4. (4) A pivot can be similarly associated to any two successive stable or unstable leaves that are not separated from above or below. We define in the same way the sets $Piv^{s}_{+}(X), Piv^{u}_{+}(X), Piv^{u}_{-}(X)$ . The set of pivots is finite. Let us also denote by

   $$ \begin{align*}Piv(X)=Piv^{s}_{+}(X)\cup Piv^{s}_{-}(X)\cup Piv^{u}_{+}(X)\cup Piv^{u}_{-}(X)\end{align*} $$
   the set of pivot periodic orbits of X.

Our first observation is that performing surgeries along the pivots does not change the branching structure.

Theorem 14. Let X be a non- ${\mathbb R}$ -covered Anosov flow, $Piv(X)$ its set of periodic pivots and $Y \in {{\mathcal S}}urg(X,Piv(X))$ . Then, under the natural identification of the orbits of Y with the orbits of X,

$$ \begin{align*}Piv^{s/u}_{\pm}(Y)=Piv^{s/u}_{\pm}(X) \quad\mbox{and}\quad {\mathcal S}^{s/u}_{\pm}(Y)={\mathcal S}^{s/u}_{\pm}(X) \end{align*} $$

As a by-product of the proof of Theorem 14 one gets that if X is an Anosov flow with oriented stable/unstable bundles, then performing surgeries on the set of orbits corresponding to lower-non-separated stable leaves cannot change the lower-non-separated stable leaves and their pivots.

Theorem 15. Consider X a non- ${\mathbb R}$ -covered Anosov flow with oriented stable/unstable bundles and Y an element of ${{\mathcal S}}urg(X,{{\mathcal S}}^{s}_{-}(X))$ . Then, under the natural identification of the orbits of Y with the orbits of X,

$$ \begin{align*}Piv(Y)^{s}_{-}=Piv^{s}_{-}(X) \quad\mbox{and}\quad {\mathcal S}^{s}_{-}(Y)={\mathcal S}^{s}_{-}(X).\end{align*} $$

The proof of both theorems is based on [Fe2] and follows from the following lemma.

Lemma 6.1.

• • Let $l_{1}$ (respectively, $l_{2}$ ) be a positive (respectively, negative) lozenge. The corner points of $l_{1}$ cannot be in the interior of $l_{2}$ .

• • Every pivot is disjoint from the interior of any lozenge.

• • Let x be a periodic point in a stable leaf not separated from below. The point x cannot belong in the interior of any pair of adjacent lozenges associated to two successive lower-non-separated stable leaves.

Proof. Assume by contradiction that a corner point of $l_{1}$ , say y, is in the interior of $l_{2}$ . Since the interior of $l_{2}$ is trivially bifoliated, the stable and unstable separatrices starting from y in the boundary of $l_{1}$ must exit $l_{2}$ . Therefore, one of the ‘missing points’ of $l_{2}$ is contained in the interior of $l_{1}$ (see Figure 12).

Figure 12 The above three cases are impossible.

The second point is a direct consequence of the first, since a pivot point is a corner point of a negative and positive lozenge (see Figure 12).

Suppose without loss of generality that x is the corner point of a negative lozenge. By the first point, x can only be contained in the interior of the negative lozenge of the pair of lozenges. But this implies that a pivot point is in the interior of the lozenge associated to x, which is impossible because of the previous point (see Figure 12).

7 Domination of the contracting holonomies

From here until §7.7, we fix a hyperbolic matrix $A\in SL(2,{\mathbb Z})$ with positive trace and eigenvalues $\lambda , \lambda ^{-1}$ satisfying $0<\lambda ^{-1}<1<\lambda $ . In §7.7 we will explain how to adapt the arguments for the case of $A\in SL(2,{\mathbb Z})$ with negative eigenvalues. We denote by X the Anosov flow which is the suspension of $f_{A}$ and its associated mapping torus $M=M_{A}$ . We fix an orientation on the stable and unstable directions $E^{s}, E^{u}$ of A, which defines an orientation on the corresponding foliations on ${\mathcal P}_{X}$ .

We begin by proving Lemma 2.1, stating that for any finite $f_{A}$ -invariant set ${\mathcal X}\subset {\mathbb T}^{2}$ , there exist finitely many orbits of primitive ${\mathcal X}$ -rectangles, for the action of the group generated by A and the integer translations.

Proof of Lemma 2.1

We give the proof for positive ${\mathcal X}$ -rectangles.

Using the $f_{A}$ -invariance, one can choose an ${\mathcal X}$ -rectangle R in each orbit so that the ratio between the lengths of the stable and unstable sides is contained in $[1,\lambda ^{2})$ .

Using the integer translations, one can also assume that the first point of the increasing diagonal of R is in $[0,1)^{2}$ .

Consider the endpoint $e(R)$ in X of the increasing diagonal of R. As $\tilde {\mathcal X}$ is discrete, if the set of such rectangles R is infinite we obtain that $e(R)$ tends to infinity. In this case, as the ratio of the lengths of the stable and unstable sides is bounded, the area of R also tends to infinity and, as a consequence of this, R contains in its interior an arbitrary number of points in $\tilde {\mathcal X}$ , which contradicts the primitive assumption on R.

7.1 If no ${\mathcal X}$ -rectangle is disjoint from $\tilde {\mathcal Y}$ the contracting holonomies dominate

In §4.6 we presented the holonomies as a dynamical game, where crossing the positive stable separatrices of points in $\tilde {\mathcal X}$ or in $\tilde {\mathcal Y}$ leads to either an expansion or a contraction. The holonomy will not always be defined when the expansion is strong. We also noticed that, in order to get two successive expansions, one needs to have a ${\mathcal X}$ -rectangle disjoint from $\tilde {\mathcal Y}$ . When no ${\mathcal X}$ -rectangle is disjoint from $\tilde {\mathcal Y}$ , the expansion due to the points in $\tilde {\mathcal X}$ can be neutralized by a sufficiently strong contraction associated to the points in $\tilde {\mathcal Y}$ . That is exactly what we prove in Theorem 8.

Theorem 8 involves proving that the hypothesis no positive primitive ${\mathcal X}$ -rectangle disjoint from $\tilde {\mathcal Y}$ implies that the contractions in the $C_{+,+}$ and $C_{-,-}$ quadrants due to (sufficiently strong) positive surgeries on ${\mathcal Y}$ dominate any surgery on ${\mathcal X}$ . The contractions in the $C_{+,-}$ and $C_{-,+}$ quadrants due to negative surgeries on ${\mathcal X}$ cannot at the same time dominate the surgeries performed on ${\mathcal Y}$ , which leads to a dynamical proof of Lemma 2.3 (which can also be proven geometrically).

If there are neither positive nor negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ then we obtain the following corollary.

Corollary 7.1. Let ${\mathcal X},{\mathcal Y}$ be two finite $f_{A}$ -invariant disjoint sets. Assume that there are no primitive X-rectangles disjoint from $\tilde {\mathcal Y}$ . Then there is $N>0$ such that, if $Y \in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ where the $n_{j}$ are of the same sign and of absolute value greater than N, then Y is ${\mathbb R}$ -covered twisted (positively or negatively, according to the sign of the $n_{j}$ ).

This is particularly interesting in view of Lemma 2.2, which proves that the hypothesis no ${\mathcal X}$ -rectangle disjoint from $\tilde {\mathcal Y}$ frequently holds. More particularly, according to the lemma, for any $f_{A}$ -invariant finite set ${\mathcal X}$ , there is $\varepsilon>0$ such that every $\varepsilon $ -dense finite invariant set ${\mathcal Y}$ intersects every ${\mathcal X}$ -rectangle.

Proof of Lemma 2.2

This is a simple consequence of the fact that there are finitely many orbits of primitive ${\mathcal X}$ -rectangles. Fix a finite family of ${\mathcal X}$ -rectangles containing one rectangle of every orbit. The lift on ${\mathbb R}^{2}$ of an $\epsilon $ -dense set ${\mathcal Y}$ will have a point in each of these finitely many rectangles, when $\epsilon $ is small enough. The lift $\tilde {\mathcal Y}$ is invariant by integer translations. If furthermore ${\mathcal Y}$ is $f_{A}$ -invariant, one gets that the lift $\tilde {\mathcal Y}$ contains a point in each primitive ${\mathcal X}$ -rectangle, hence in every ${\mathcal X}$ -rectangle.

Remark 7.1. If in Lemma 2.2 one chooses $\varepsilon>0$ very small, then $\tilde {\mathcal Y}$ will have an abundance of points in any ${\mathcal X}$ -rectangle and even in any $ 1/K$ -homothetic subrectangle for any arbitrary choice of $K>1$ .

The frequency of crossing the separatrices of points in ${\mathcal Y}$ can counterbalance a possible lack of strength of the contractions associated to ${\mathcal Y}$ , which is the basic idea behind the proof of Theorem 7.

Our aim from now on is to prove Theorems 8 and 7: assuming the lack of positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ , strong positive surgeries along ${\mathcal Y}$ generate ${\mathbb R}$ -covered positively twisted Anosov flows.

In order to do so, we will use the fact that a flow Y is ${\mathbb R}$ -covered (trivially or positively twisted) if every $C_{+,+}$ and $C_{-,-}$ quadrant at every point of ${\mathcal P}_{Y}$ is complete. Then we will discard the trivial case, getting the positive twist property.

We start by proving the completeness at all points in $\tilde {\mathcal X}$ .

7.2 Completeness of the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ for $x\in \tilde {\mathcal X}$ , for large surgeries on ${\mathcal Y}$

In this section we will prove the following result.

Proposition 7.1. Assume that ${\mathcal X}$ and ${\mathcal Y}$ are two finite invariant sets such that there are no positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ . Then there is $N>0$ such that if $Y\in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ and $n_{j}> N$ , then at every $x\in \tilde {\mathcal X}$ the quadrant $C_{+,+}(x)$ is complete. The same holds for the quadrant $C_{-,-}(x)$ .

Let us parametrize the positive stable separatrices of points in $\tilde {{\mathcal X}}$ . $\tilde {{\mathcal X}}$ is the union of a finite number of $\pi _{1}(M)$ -orbits. Take a representative $x_{1},\ldots ,x_{n}$ of each orbit and identify $F^{s}_{+}(x_{i})$ with $[0,+\infty )$ in an affine way. Take for every $x\in \tilde {{\mathcal X}}\setminus \{x_{1},\ldots ,x_{n}\}$ an element $\gamma _{x} \in \pi _{1}(M)$ such that $x= \theta _{X}(\gamma _{x})(x_{i})$ for some i. Using the $\theta _{X}(\gamma _{x})$ , we can parametrize in an affine way all the $F^{s}_{+}(x)$ with $x\in \tilde {{\mathcal X}}$ .

Consider $x\in \tilde {\mathcal X}$ . Thanks to the previous paragraph we can identify $F^{s}_{+}(x)$ with $[0,+\infty )$ . A primitive positive $({\mathcal X},x)$ -rectangle is a primitive positive ${\mathcal X}$ -rectangle whose increasing diagonal has its origin on x. Any primitive positive $({\mathcal X},x)$ -rectangle R is uniquely determined by its base segment $[0,\mu _{R}]:=R\cap F^{s}_{+}(x)$ .

To every $t\in [0,+\infty )$ one associates the primitive $({\mathcal X},x)$ -rectangle $R_{x}(t)$ with the largest base segment, which does not contain t in its interior. The base segment of this rectangle is equal to $[0,\mu _{x}(t)]$ , where $\mu _{x}(t)= \max \{\mu _{R}\leq t\}$ .

Similarly, one can define the primitive $({\mathcal X},x)$ -rectangle with the smallest base segment containing t in its interior and $\nu _{x}(t)=\min \{\mu (R)>t\}$ . $\mu _{x}$ and $\nu _{x}$ are well defined thanks to Lemma 2.1.

One denotes $\rho _{x}(t)$ the positive number such that the point $(\mu _{x}(t),\rho _{x}(t))\in \tilde {\mathcal X}\cap R_{x}(t)$ is the endpoint of the positive diagonal of the rectangle $R_{x}(t)$ .

By assumption on ${\mathcal X},{\mathcal Y}$ , the rectangle $R_{x}(t)$ contains a point of $\tilde {\mathcal Y}$ in its interior. We consider the smallest first coordinate of such a point; more precisely, we denote by $\delta _{x}(t)$ the smallest $r>0$ such that there is $(r,s)\in \tilde {\mathcal Y}\cap R_{x}(t)$ . Clearly, we have

$$ \begin{align*}0<\delta_{x}(t)<\mu_{x}(t).\end{align*} $$

Lemma 7.1. Recall that $\lambda>1$ is the expansive eigenvalue of A. There is N such that for every $t>0$ , every $x\in \tilde {\mathcal X}$ and every $n\geq N$ ,

$$ \begin{align*}\mu_{x}(\delta_{x}(t)+ \lambda^{-n}(t-\delta_{x}(t)))=\mu_{x}(\delta_{x}(t)).\end{align*} $$

Proof. Just notice that the functions $\mu _{x},\delta _{x}$ are equivariant under multiplication by $\lambda ^{\pi }$ , where $\pi $ is a common multiple of the periods of points in ${\mathcal X},{\mathcal Y}$ . Notice also that because of our choice of parametrization, if the lemma stands for $x\in \tilde {{\mathcal X}}$ it also stands for every point in its $\pi _{1}(M)$ -orbit.

So we only need to prove the lemma for t in the interval $[1,\lambda ^{\pi }]$ and for a finite number of points in $\tilde {{\mathcal X}}$ , therefore for a finite number of intervals $[\mu _{x}(t),\nu _{x}(t))$ .

For n large enough $\delta _{x}(t)+ \lambda ^{-n}(\nu _{x}(t)-\delta _{x}(t))$ is very close to $\delta _{x}(t)$ (see Figure 13), and since the function $\mu _{x}$ is constant on an interval of the form $[\delta _{x}(t), \delta _{x}(t)+\epsilon ]$ we get the desired result.

Figure 13 In this figure red points ( ) represent points in $\tilde {\mathcal Y}$ and blue ones ( ) points in $\tilde {\mathcal X}$ . Colour available online.

Proof of Proposition 7.1

Fix N given by Lemma 7.1 and $x\in \tilde {{\mathcal X}}$ . Let $Y\in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y}, \ast , (n_{j})_{j\in J})$ with $n_{j}> N$ . Consider the positive unstable separatrix through the point $t\in F^{s}_{+}(x)$ (see Figure 14). One follows it starting at t. The first point of $\tilde {\mathcal X}\cap C_{+,+}(x)$ whose positive stable separatrix we meet is the point $x_{0}=(\mu _{x}(t),\rho _{x}(t))$ . However, before that, we meet the positive separatrices of all the points in $\tilde {\mathcal Y}\cap R_{x}(t)$ and perhaps of some points of $\tilde {\mathcal Y}$ outside $R_{x}(t)$ . The holonomy of the vector field Y obtained by surgery involves changing the intersection point each time by multiplying the distance to the point in $\tilde {\mathcal Y}$ by a factor $\lambda ^{-n}$ (where n is the product of the characteristic number and the period) which by hypothesis is smaller than $\lambda ^{-N}$ . Thus, according to Lemma 7.1, by playing the holonomy game we reach the stable manifold of $x_{0}=(\mu _{x}(t),\rho _{x}(t))$ at a point $(t_{1},\rho _{x}(t))$ with

$$ \begin{align*}\mu_{x}(t_{1})=\mu_{x}(\delta_{x}(t))<\mu_{x}(t).\end{align*} $$

In particular, $(t_{1},\rho _{x}(t))$ is on the negative stable separatrix of $x_{0}$ and therefore is not affected by the surgery on that point.

Figure 14 In this figure red points ( ) represent points in $\tilde {\mathcal X}$ and blue ones ( ) points in $\tilde {\mathcal Y}$ . Colour available online.

We proceed by following the positive unstable separatrix of the point $(t_{1},\rho _{x}(t))$ . Let $x_{1}$ be the first point of $\tilde X\cap C_{+,+}(x)$ whose positive stable separatrix meets the positive unstable separatrix of $(t_{1},\rho _{x}(t))$ . It is easy to see that $x_{1}=(\mu _{x}(t_{1}),\rho _{x}(t_{1}))$ .

Again, by assumption there are points of $\tilde {\mathcal Y}$ in $R_{x}(t_{1})$ . But since $\mu _{x}(t_{1})=\mu _{x}(\delta _{x}(t))<\delta _{x}(t)$ the points in $\tilde {\mathcal Y}\cap R_{x}(t_{1})$ are not in $R_{x}(t)$ .

Similarly, by playing the holonomy game we will reach the stable manifold of $x_{1}=(\mu _{x}(t_{1}),\rho _{x}(t_{1}))$ at a point $(t_{2},\rho _{x}(t_{1}))$ with $\mu _{x}(t_{2})=\mu _{x}(\delta _{x}(t_{1}))<\mu _{x}(t_{1})$ . In particular, the point $(t_{2},\rho _{x}(t_{1}))$ is on the negative separatrix of $x_{1}$ and is not affected by the surgery on ${\mathcal X}$ .

We proceed in the same way. By finite induction, we obtain a primitive rectangle $R_{x}(t_{i})$ in the orbit of $R_{x}(t)$ and after this the procedure will become periodic modulo iteration by a power of A. In particular, while we play the holonomy game, the positive unstable separatrix of t will come closer and closer to $F^{u}_{X}(x)$ .

This shows that the positive unstable separatrix of t intersects the positive stable separatrix of every point in the positive unstable separatrix of x. Therefore, the $(+,+)$ -quadrant at the point x is complete, which concludes the proof.

Notice that the notion of positive ${\mathcal X}$ -rectangle is the same for the quadrants $(+,+)$ and $(-,-)$ . Therefore the same argument proves the completeness of the quadrant $C_{-,-}(x)$ for $x\in \tilde {\mathcal X}$ .

7.3 Completeness of the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ for $x\in \tilde {\mathcal X}$ : replacing strong surgeries by the $\varepsilon $ -density of ${\mathcal Y}$

Proposition 7.2. Assume that ${\mathcal X}$ is a finite $f_{A}$ -invariant set. Then there is a $\varepsilon>0$ such that for any $\varepsilon $ -dense finite $f_{A}$ -invariant set ${\mathcal Y}$ , one has the following property: if $Y\in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ and $n_{j}>0$ , then for every $x\in \tilde {\mathcal X}$ the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ are complete.

Using the fact that the orbits of primitive ${\mathcal X}$ -rectangles are finitely many, one gets $\varepsilon _{0}>0$ such that every $\varepsilon _{0}$ -dense periodic orbit ${\mathcal Y}_{0}$ intersects every ${\mathcal X}$ -rectangle. We fix such a ${\mathcal Y}_{0}$ .

Fix $N>0$ given by Proposition 7.1. We denote by $\mu $ the product of N and the period of ${\mathcal Y}_{0}$ :

$$ \begin{align*}\mu=N\cdot \pi({\mathcal Y}_{0}).\end{align*} $$

Lemma 7.2. Take $K\in \mathbb {N}$ . There is $\varepsilon>0$ such that, for every $\varepsilon $ -dense $f_{A}$ -invariant finite set ${\mathcal Y}$ , for any $x\in \tilde {\mathcal X}$ and for any primitive positive $({\mathcal X},x)$ -rectangle ${\mathcal R}$ , there are at least K points $y\in \tilde {\mathcal Y}\cap {\mathcal R}$ with the following properties:

• • the period of y is greater than $\mu $ ;

• • y belongs to the connected component of ${\mathcal R}\setminus \bigcup _{y_{0}\in \tilde {\mathcal Y}_{0}\cap {\mathcal R}} F^{u}_{X}(y_{0})$ which is bounded on one side by $F^{u}_{X}(x)$ ;

• • y belongs to ${\mathcal R}\setminus \bigcup {\mathcal R}_{i}$ , where the ${\mathcal R}_{i}$ are the positive primitive $({\mathcal X},x)$ -rectangles having a strictly larger base than ${\mathcal R}$ .

Proof. We choose a rectangle R in each orbit of primitive ${\mathcal X}$ -rectangles. We just need to prove the statement for this finite collection of $({\mathcal X},x)$ -rectangles ${\mathcal R}$ . One still gets a finite collection of rectangles by considering ${\mathcal R}\setminus \bigcup {\mathcal R}_{i}$ where ${\mathcal R}_{i}$ are the positive primitive $({\mathcal X},x)$ -rectangles having a strictly larger base than ${\mathcal R}$ .

The second and third properties are granted by the $\varepsilon $ density. Furthermore, if $\varepsilon $ is sufficiently small, any periodic point $\varepsilon $ -close to $F^{u}_{X}(x)\cap R$ has period greater than $\mu $ .

Proof of Proposition 7.2

Fix $x\in \tilde {\mathcal X}$ . Consider for every $t\in F_{+}^{s}(x)$ the rectangle whose base is $[0,\nu _{x}(t)]$ and whose height is $\rho _{x}(t)$ . We will denote this rectangle by $R^{\mathrm {ext}}_{x}(t)$ . Notice that thanks to the definition of $\mu _{x},\nu _{x},\rho _{x}$ , we have that $ R^{\mathrm {ext}}_{x}(t) \cap \tilde {{\mathcal X}} = \big (R_{x}(t) \cup R_{x}(\nu _{x}(t))\big )\cap \tilde {{\mathcal X}}$ . In particular, since $R_{x}(t)$ and $R_{x}(\nu _{x}(t))$ are primitive, $R^{\mathrm {ext}}_{x}(t)\cap \tilde {{\mathcal X}}$ consists of three points: x, $(\mu _{x}(t),\rho _{x}(t))$ and $\big (\mu _{x}(\nu _{x}(t)),\rho _{x}(\nu _{x}(t))\big )$ .

Since there are finitely many orbits of primitive ${\mathcal X}$ -rectangles (for the action of $\pi _{1}(M)$ ), the set $\bigcup _{x\in \tilde {{\mathcal X}}}\bigcup _{t\in \mathbb {R}}\lbrace R^{\mathrm {ext}}_{x}(t)\rbrace $ consists also of a finite number of $\pi _{1}(M)$ -orbits. Because of our previous argument and the fact that $\tilde {{\mathcal Y}_{0}}$ is $\pi _{1}(M)$ -invariant, the maximum number of points of $\tilde {\mathcal Y}_{0}$ in any $R^{\mathrm {ext}}_{x}(t)$ is finite. We denote it by K.

Take $\epsilon , {\mathcal Y}$ given by Lemma 7.2 applied for K. We will compare the holonomy game for a vector field Y obtained by positive surgeries along ${\mathcal Y}$ and the vector field $Y_{0}$ obtained by surgeries along ${\mathcal Y}_{0}$ of characteristic number N. Roughly speaking, we will check that the holonomy of Y is more contracting than that of $Y_{0}$ , which will finish the proof.

Fix $t\in F_{+}^{s}(x)$ and consider $t^{\prime }=\big (t, \rho _{x}(\nu _{x}(t))\big )$ . Since $R_{x}(\nu _{x}(t))$ is a primitive ${\mathcal X}$ -rectangle, it does not contain any point of $\tilde {{\mathcal X}}$ in its interior and therefore

$$ \begin{align*}h_{Y,x,\rho_{x}(\nu_{x}(t))}(t)\leq t^{\prime}.\end{align*} $$

Hence for every $q>\rho _{x}(\nu _{x}(t))$ ,

$$ \begin{align*}h_{Y,x,q}(t)\leq h_{Y,\rho_{x}(\nu_{x}(t)),q}(t^{\prime}).\end{align*} $$

It therefore suffices to prove that the holonomy of $t^{\prime }$ for Y is ‘more contracting’ than the holonomy of t for $Y_{0}$ . More precisely, it suffices to prove that for some sequence $q_{i} \rightarrow +\infty $ with $q_{i}>\rho _{x}(\nu _{x}(t))$ we have

(1) $$ \begin{align} h_{Y,\rho_{x}(\nu_{x}(t)),q_{i}}(t^{\prime})\leq h_{Y_{0},x,q_{i}}(t) \end{align} $$

In the proof of Proposition 7.1, we defined by induction a sequence of points $x_{i}=(\mu _{x}(t_{i}),\rho _{x}(t_{i}))\in \tilde {{\mathcal X}}$ (where $t_{0}=t$ ), which are the successive points of $\tilde {\mathcal X}\cap C_{+,+}(x)$ appearing in the game for $Y_{0}$ . We choose $q_{i}=\rho _{x}(t_{i})$ . Let us now play the game for Y and show (1) for this choice of $q_{i}$ .

We follow the positive unstable separatrix of $t^{\prime }$ starting from $t^{\prime }$ . The first point in $\tilde {\mathcal X}\cap C_{+,+}(x)$ whose positive stable separatrix we meet is $x_{0}$ , as in the game for $Y_{0}$ . Before that, we meet the positive separatrices of all the points in $\tilde {\mathcal Y}\cap (R^{\mathrm {ext}}_{x}(t)-R_{x}(\nu _{x}(t)))$ . In the game for $Y_{0}$ there were at most K points of $\tilde {{\mathcal Y}_{0}}$ in $R^{\mathrm {ext}}_{x}(t)$ , and in the game for Y there are at least K of these points in the connected component of $R_{x}(t)\setminus \bigcup _{y_{0}\in \tilde {\mathcal Y}_{0}\cap R_{x}(t)} F^{u}_{X}(y_{0})$ which is bounded on one side by $F^{u}_{X}(x)$ .

The holonomy of the vector field Y obtained by surgery involves changing the intersection point each time by multiplying the distance to the point in $\tilde {\mathcal Y}$ by a factor $\lambda ^{-n}$ (where n is the product of the characteristic number and the period) which by hypothesis is smaller than $\lambda ^{-\mu }$ .

It is now easy to check that the two previous paragraphs imply

(2) $$ \begin{align} h^{u}_{Y,\rho_{x}(\nu_{x}(t)),q_{0}}(t^{\prime})<h^{u}_{Y_{0},x,q_{0}}(t). \end{align} $$

We denote by $t^{\prime }_{1}$ the point $(h^{u}_{Y_{0},x,q_{0}}(t),q_{0})=(t_{1},q_{0})$ . We repeat the same argument for $t_{1}^{\prime }$ and $t_{1}$ . We therefore get

(3) $$ \begin{align} h^{u}_{Y,q_{0},q_{1}}(t_{1}^{\prime})<h^{u}_{Y_{0},x,q_{1}}(t_{1}). \end{align} $$

Using (2) and the fact that $t_{1}<t$ , we have that

(4) $$ \begin{align} h^{u}_{Y_{0},x,q_{1}}(t_{1})&\leq h^{u}_{Y_{0},x,q_{1}}(t), \end{align} $$

(5) $$ \begin{align} h^{u}_{Y,\rho_{x}(\nu_{x}(t)),q_{1}}(t^{\prime})&\leq h^{u}_{Y,q_{0},q_{1}}(t^{\prime}_{1}). \end{align} $$

Finally, by combining (3)–(5), we get the desired inequality

$$ \begin{align*}h^{u}_{Y,\rho_{x}(\nu_{x}(t)),q_{1}}(t^{\prime})\leq h^{u}_{Y_{0},x,q_{1}}(t).\end{align*} $$

We denote by $t^{\prime }_{n}$ the point $(h^{u}_{Y_{0},x,q_{n-1}}(t),q_{n-1})=(t_{n},q_{n-1})$ and we proceed by induction in order to prove the desired inequality.

7.4 Completeness of the $(+,+)$ -quadrants at every point

The aim of this section is to deduce from Proposition 7.1 that every $(+,+)$ and $(-,-)$ quadrant at any point of $P_{Y}$ is complete.

Proposition 7.3. Let ${\mathcal X},{\mathcal Y}$ be two disjoint finite $f_{A}$ -invariant sets, and let $Y\in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ be any vector field with $n_{j}\geq 0$ . If for any $x\in \tilde {\mathcal X}$ the quadrant $C_{+,+}(x)$ is complete, then for any $z\in {\mathcal P}_{Y}$ the quadrant $C_{+,+}(z)$ is also complete.

As a straightforward consequence of Propositions 7.1, 7.2 and 7.3 we obtain the following corollary.

Corollary 7.2. With the hypothesis of Proposition 7.1 or Proposition 7.2 the quadrants $C_{+,+}(z)$ and $C_{-,-}(z)$ are complete for any point $z\in {\mathcal P}_{Y}$ .

Proof of Proposition 7.3

Assume by contradiction that there is $p\in {\mathcal P}_{Y}$ for which the quadrant $C_{+,+}(p)$ is not complete. Therefore, there exist $r\in W^{u}_{+}(p)$ and $t_{0}\in W^{s}_{+}(p)$ such that the stable positive separatrix $W^{s}_{+}(r)$ and the unstable positive separatrix $W^{u}_{+}(t_{0})$ do not intersect.

Note that the set of unstable leaves cutting a stable leaf is open, as the intersections are transversal. Thus the leaves which do not cut $W^{s}_{+}(r)$ form a closed set which does not contain p. Therefore, there is a smallest $t>0$ for which $W^{u}_{+}(t)$ does not cut $W^{s}_{+}(r)$ .

If this unstable leaf does not cut the positive stable separatrix of a point in $\tilde {\mathcal X} \cap C_{+,+}(p)$ , then the unstable holonomy ${h^{u}_{Y,p,r}}$ restricted on $[0,t]$ is well defined and its image is contained in $([0,t], r)$ . Hence, by our initial hypothesis, there is $x\in \tilde {\mathcal X}\cap C_{+,+}(p)$ such that $W^{u}_{+}(t)$ cuts $W^{s}_{+}(x)$ and thus enters the quadrant $C_{+,+}(x)$ .

If $W^{s}_{+}(r)$ crosses $W^{u}_{+}(x)$ (see Figure 15), then as the quadrant $C_{+,+}(x)$ is by assumption complete, $W^{s}_{+}(r)$ cuts $W^{u}_{+}(t)$ , thus contradicting the hypothesis.

Figure 15 If $W_+^s(r)$ enters $C_{+,+}(x)$ , then it will intersect $W_+^u(t)$ . Colour available online.

Therefore, $W^{s}_{+}(r)$ cannot cross $W^{u}_{+}(x)$ . Now the holonomy from $[0,t]$ to $W^{s}(x)$ is well defined and contains x in its image. Hence, $W^{u}_{-}(x)$ cuts $W^{s}_{+}(p)$ at some point $t_{0}<t$ , which means by our previous hypothesis that $W^{u}_{+}(t_{0})$ does not cut $W^{s}_{+}(r)$ . This contradicts the minimality of t and concludes the proof of the corollary.

7.5 ${\mathbb R}$ -covered

Using Corollary 7.2, we obtain the following result.

Corollary 7.3. Under the hypotheses of Propositions 7.1 or 7.2 the flow Y is ${\mathbb R}$ -covered and positively twisted.

Proof. An Anosov flow for which every $(+,+)$ and $(-,-)$ quadrant is complete is ${\mathbb R}$ -covered and not negatively twisted. By our proofs of Propositions 7.1 or 7.2 the completeness of the $(+,+)$ and $(-,-)$ quadrants does not depend on the surgeries performed on ${\mathcal X}$ . However, if Y were non-twisted, a negative surgery on ${\mathcal X}$ would create a negatively twisted ${\mathbb R}$ -covered field. So Y needs to be twisted.

This concludes the proof of Theorems 8 and 7 and hence also of Theorem 4.

7.6 On the existence of rectangles: proof of Lemma 2.3

Proof. Assume that every positive ${\mathcal X}$ -rectangle contains points in $\tilde {\mathcal Y}$ and every negative ${\mathcal Y}$ -rectangle contains point in $\tilde {\mathcal X}$ . Then strong negative surgeries on ${\mathcal X}$ and positive on ${\mathcal Y}$ would induce flows which are ${\mathbb R}$ -covered with all quadrants complete (according to Proposition 7.1), that is, with trivial bifoliated planes. Performing stronger negative surgeries on ${\mathcal X}$ would not change this property, thus contradicting [Fe1].

7.7 The case of matrices with negative eigenvalues

In this section we consider a hyperbolic matrix $B\in SL(2,{\mathbb Z})$ with negative eigenvalues and where $X_{B}$ is the suspension flow of $f_{B}$ on the manifold $M_{B}$ , the mapping torus of $f_{B}$ . Let $A=B^{2}$ and denote by $X_{A}$ the suspension flow of $f_{A}$ on $M_{A}$ . The matrix A is hyperbolic with positive eigenvalues and $M_{A}$ is the $2$ -fold cover of the orientations of the stable/unstable bundles of $X_{B}$ . The Anosov flow $X_{A}$ is the lift of $X_{B}$ on $M_{A}$ .

We consider two finite $f_{B}$ -invariant disjoint sets ${\mathcal X}, {\mathcal Y}$ and we assume that every positive ${\mathcal X}$ -rectangle intersects $\tilde {\mathcal Y}$ .

We denote by ${\mathcal X}_{A}$ , ${\mathcal Y}_{A}$ the lifts of ${\mathcal X}$ , ${\mathcal Y}$ on $M_{A}$ . Note that the bifoliated plane $({\mathcal P}_{X_{A}},F^{s}_{X_{A}},F^{u}_{X_{A}})$ is canonically identified with $({\mathcal P}_{X_{B}},F^{s}_{X_{B}},F^{u}_{X_{B}})$ and the lifts of ${\mathcal X}_{A},{\mathcal Y}_{A}$ on ${\mathcal P}_{X_{A}}$ are $\tilde {\mathcal X}$ , $\tilde {\mathcal Y}$ , respectively.

Remark 7.2. Every positive ${\mathcal X}$ -rectangle contains a point in $\tilde {\mathcal Y}$ if and only if every positive ${\mathcal X}_{A}$ -rectangle contains a point in $\tilde {\mathcal Y}$ .

Proof of Theorems 8, 7 and 4 for matrices with negative eigenvalues

According to Remark 7.2, the hypotheses for $X_{B}, {\mathcal X},{\mathcal Y}$ imply that every positive ${\mathcal X}_{A}$ -rectangle contains a point in $\tilde {\mathcal Y}$ , so $X_{A},{\mathcal X}_{A},{\mathcal Y}_{A}$ satisfy the hypotheses of Theorem 8 for matrices with positive eigenvalues. Thus, there is $N>0$ such that every Anosov flow in ${{\mathcal S}}urg(X,{\mathcal X}_{A},{\mathcal Y}_{A},\ast , (\nu _{j})_{j\in J})$ with $\nu _{j}\geq N$ is ${\mathbb R}$ -covered and positively twisted.

The lift $Y_{A}$ on the bundles orientation cover of every Anosov flow Y in ${{\mathcal S}}urg(X_{B},{\mathcal X},{\mathcal Y}, \ast , (n_{j})_{j\in J})$ with $n_{j}\geq N$ belongs to ${{\mathcal S}}urg(X_{A},{\mathcal X}_{A},{\mathcal Y}_{A},\ast , (\hat n_{j})_{j\in J})$ with $\hat n_{j}\geq N$ (see Remark 4.1). Thus $Y_{A}$ is ${\mathbb R}$ -covered and positively twisted and therefore Y is also ${\mathbb R}$ -covered and positively twisted. This concludes the proof of Theorem 8 for matrices with negative eigenvalues.

Now let us move on to the proof of Theorem 7, which will imply Theorem 4.

Observe that for any finite $f_{B}$ -invariant set ${\mathcal Y}$ , if ${\mathcal Y}$ is $\varepsilon $ -dense then $ {\mathcal Y}_{A}$ is $\varepsilon $ -dense. We fix $\varepsilon $ so that, given any $\varepsilon $ -dense ${\mathcal Y}$ , Theorem 7 for matrices with positive eigenvalues implies that any flow in $ {{\mathcal S}}urg(X_{A},{\mathcal X}_{A},{\mathcal Y}_{A},\ast , (\nu _{j})_{j\in J})$ with $ \nu _{j}\geq 1$ (respectively, $\nu _{j}\leq -1$ ) is ${\mathbb R}$ -covered and positively (respectively, negatively) twisted.

The lift $Y_{A}$ of any $ Y\in {{\mathcal S}}urg(X_{B},{\mathcal X},{\mathcal Y},\ast , (n_{j})_{j\in J})$ with $ n_{j}\geq 1$ (respectively, $ n_{j}\leq -1$ ) belongs to ${{\mathcal S}}urg(X_{A},{\mathcal X}_{A},{\mathcal Y}_{A},\ast , (\hat n_{j})_{j\in J})$ with $\hat n_{j}\geq 1$ (respectively, $\hat n_{j}\leq -1$ ). We conclude that $Y_{A}$ and therefore Y are ${\mathbb R}$ -covered twisted according to the sign of the surgeries performed on ${\mathcal Y}$ . This concludes the proof of Theorem 7 and therefore of Theorem 4 for matrices with negative eigenvalues.

8 Domination of expanding holonomies: strings of ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$

From here until §8.7, similarly to §7, we fix a hyperbolic matrix $A\in SL(2,{\mathbb Z})$ with positive eigenvalues $0<\lambda ^{-1}<1<\lambda $ . In §8.7 we will explain how our arguments can be adapted for the case of $A\in SL(2,{\mathbb Z})$ with negative eigenvalues.

Our aim in this section is to prove Theorems 5, 6 and 9. We start by proving Theorem 9. Going from Theorem 9 to Theorems 5 and 6 is a process that is analogous to the one we followed to go from Theorem 8 to Theorems 7 and 4.

Therefore, in addition to Theorem 9, in order to prove Theorems 5 and 6, we will need two more things. The first is following theorem, which will be proved later in this section.

Theorem 16. For any hyperbolic matrix $A\in SL(2,{\mathbb Z})$ there are two periodic orbits ${\mathcal X}$ and ${\mathcal Y}$ such that there exist positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and negative ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ .

The second is to replace the hypothesis of large characteristic numbers in Theorem 9 by a large period as in the case of Theorems 4 and 7.

8.1 Main step for Theorem 9: undertwisted quadrants

Let ${\mathcal X}$ be a finite $f_{A}$ -invariant set. A string of positive ${\mathcal X}$ -rectangles or a positive ${\mathcal X}$ -string is a family of positive ${\mathcal X}$ -rectangles $R_{i}$ indexed by ${\mathbb N}$ such that for any $k\in {\mathbb N}$ the intersection $R_{i}\cap R_{i+1}$ is the endpoint of the increasing diagonal of $R_{i}$ and the initial point of the increasing diagonal of $R_{i+1}$ . The origin of the increasing diagonal of $R_{0}$ is called the origin of the string.

Remark 8.1. Let ${\mathcal X}$ be a periodic orbit for $f_{A}$ and ${\mathcal Y}$ a finite $f_{A}$ -invariant set disjoint from ${\mathcal X}$ . The existence of a positive (respectively, negative) ${\mathcal X}$ -string disjoint from $\tilde {\mathcal Y}$ is equivalent to the existence of a positive (respectively, negative) ${\mathcal X}$ -rectangle disjoint from $\tilde {\mathcal Y}$ . Indeed, given one ${\mathcal X}$ -rectangle R disjoint from $\tilde {\mathcal Y}$ , by eventually breaking it, we can assume that it is primitive. Now we can consider its image by $g\in \pi _{1}(M)$ , where g sends one of the points of $\tilde {{\mathcal X}}\cap R $ to the other, and thus construct a string by induction.

Theorem 9 is a consequence of the following technical result.

Theorem 17. Let $A\in SL(2,{\mathbb Z})$ be a hyperbolic matrix, and let ${\mathcal X}$ and ${\mathcal Y}$ be finite $f_{A}$ -invariant sets such that there exists a positive ${\mathcal X}$ -string disjoint from $\tilde {\mathcal Y}$ . Then there is $n>0$ such that for any $Y \in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},(m_{i})_{i\in I}, \ast )$ with $m_{i}<-n$ , there is $x\in \tilde {\mathcal X}$ such that the quadrants $C_{+,+}(x)$ and $C_{-,-}(x)$ are incomplete (that is, undertwisted).

The important point in the statement of Theorem 17 is that the conclusion does not depend on the surgeries performed (or not) on the orbits of the points in ${\mathcal Y}$ .

Proof of Theorem 9 assuming Theorem 17

The hypotheses of Theorem 9 allow us to apply Theorem 17 for the quadrants $C_{+,+}$ and $C_{-,-}$ , but also the quadrants $C_{+,-}$ and $C_{-,+}$ by exchanging the roles of ${\mathcal X}$ and ${\mathcal Y}$ . Therefore there is $n>0$ such that for all surgeries on ${\mathcal X}$ and ${\mathcal Y}$ with negative characteristic numbers on ${\mathcal X}$ and positive on ${\mathcal Y}$ , all of absolute value greater than n, there exist a point $x\in \tilde {\mathcal X}$ and a point $y\in \tilde {\mathcal Y}$ such that the quadrants $C_{+,+}(x)$ and $C_{+,-}(y)$ are both undertwisted. This implies that Y is not ${\mathbb R}$ -covered, which finishes the proof.

8.2 Proof of Theorem 17: ${\mathcal X}$ -staircase disjoint from $\tilde {\mathcal Y}$

We consider ${\mathbb R}^{2}$ endowed with a (linear) base in which ${\mathcal F}^{s}$ is the horizontal foliation, ${\mathcal F}^{u}$ is the vertical foliation and the origin $(0,0)$ belongs to $\tilde X$ . For the sake of simplicity we will assume that the eigenvalues of A are positive, but indeed the arguments that follow can also be adapted for the case of negative eigenvalues. We denote by $\lambda>1$ and $\lambda ^{-1}<1$ the two eigenvalues of A. Fix m to be the twist function for X and n the twist function for Y, that is, the product of the characteristic number and the period for $f_{A}$ . We have that $m(f_{A}(x))= m(x)$ and $n(f_{A}(x))= n(x)$ .

Recall that the stable and unstable foliations are oriented. Hence, every rectangle R has a top side $\partial ^{s,\mathrm {up}}R$ , a bottom side $\partial ^{s,\mathrm {low}}R$ , a right side $\partial ^{u,\mathrm {right}}R$ and a left side $\partial ^{u,\mathrm {left}} R$ .

A horizontal(respectively, vertical) subrectangle of R is a rectangle $R_{0}\subset R$ such that $\partial ^{u}(R_{0})\subset \partial ^{u}(R)$ (respectively, $\partial ^{s}(R_{0})\subset \partial ^{s}(R)$ ).

Furthermore, we will say that a vertical subrectangle is a right vertical subrectangle if

$$ \begin{align*}\partial^{u,\mathrm{right}}(R_{0})=\partial^{u,\mathrm{right}}(R).\end{align*} $$

Given a rectangle R, we denote by $\ell ^{s}(R)$ the length of its stable (top or bottom) sides and $\ell ^{u}(R)$ the length of the unstable (right or left) sides.

Definition 8.1. Fix $x\in \tilde X$ . We say that an infinite sequence of rectangles ${\mathcal R}_{0},{\mathcal R}_{1},\ldots $ is a positive ${\mathcal X}$ -staircase with origin at $x\in \tilde X$ in $C_{+,+}(x)$ (or a $({\mathcal X},x,+,+)$ -staircase) if the following conditions are satisfied (see Figure 16).

1. (1) All rectangles ${\mathcal R}_{n}$ are contained in $C_{+,+}(x)$ .

2. (2) There is a positive ${\mathcal X}$ -string $\{\Delta _{i}\}_{i\in {\mathbb N}}$ with origin at x such that $\Delta _{i}$ is a right vertical subrectangle of $R_{i}$ for every $i>0$ and $R_{0}=\Delta _{0}$ .

3. (3) $ \partial ^{s,\mathrm {up}}{\mathcal R}_{m} \subset \partial ^{s,\mathrm {low}} {\mathcal R}_{m+1}$

4. (4) ${\ell ^{s}(\Delta _{i+1}) }/{\ell ^{s}(\Delta _{i})}$ is bounded for $i\in {\mathbb N}$ .

Figure 16 A positive ${\mathcal X}$ -staircase. Colour available online.

In a similar way, one can define a positive staircase inside $C_{-,-}(x)$ and negative staircases in $C_{+,-}(x)$ and $C_{-,+}(x)$ .

Remark 8.2. By definition, the left unstable sides $\partial ^{u,\mathrm {left}}(R_{i})$ of all the rectangles $R_{i}$ in a positive $({\mathcal X},x,+,+)$ -staircase ${\mathcal R}=\{R_{i}\}_{i\in {\mathbb N}}$ are segments on $F^{u}_{+}(x)$ which are adjacent (disjoint interior but sharing an endpoint with the next one), whose the union is an interval ${\mathcal I}^{u}({\mathcal R})$ on $F^{u}_{+}(x)$ starting at x:

$$ \begin{align*}{\mathcal I}^{u}({\mathcal R})=\bigcup_{i=0}^{\infty} \partial^{u,\mathrm{left}}(R_{i}).\end{align*} $$

We say that ${\mathcal I}^{u}({\mathcal R})$ is the axis of the staircase ${\mathcal R}$ .

Remark 8.3. We also have that

$$ \begin{align*}\ell^{s}(R_{i})=\sum_{j=0}^{i}\ell^{s}(\Delta_{j}).\end{align*} $$

Theorem 17 is a simple consequence of the next two lemmas.

Lemma 8.1. If there is a positive ${\mathcal X}$ -string $\{\Delta _{i}\}_{i\in \mathbb {N}}$ disjoint from $\tilde {\mathcal Y}$ with origin at $x\in \tilde {\mathcal X}$ , then there exists a positive ${\mathcal X}$ -staircase disjoint from $\tilde {\mathcal Y}$ with origin at x inside $C_{+,+}(x)$ .

Lemma 8.2. If for some point $x \in \tilde {{\mathcal X}}$ there exists a positive ${\mathcal X}$ -staircase $(R_{i})_{i \in \mathbb {N}}$ disjoint from $\tilde {\mathcal Y}$ with origin at x in $C_{+,+}(x)$ , then there exists $N^{\prime }>0$ such that for any $Y \in {{\mathcal S}}urg(X_{A},{\mathcal X},{\mathcal Y},(m_{i})_{i\in I},\ast )$ with $m_{i}<-N^{\prime }$ the $C_{+,+}(x)$ quadrant for Y is undertwisted (that is, incomplete).

8.3 ${\mathcal X}$ -strings and ${\mathcal X}$ -staircase disjoint for $\tilde {{\mathcal Y}}$

Proof of Lemma 8.1

Let $\tilde {\mathcal X}$ and $\tilde {\mathcal Y}$ be two finite invariant sets and assume that $\{\Delta _{i}\}_{i\in {\mathbb N}}$ is a positive ${\mathcal X}$ -string disjoint from $\tilde {{\mathcal Y}}$ with origin at a point $x_{0}\in \tilde {\mathcal X}$ . By eventually breaking some of the $\Delta _{i}$ , we can assume without loss of generality that the $\Delta _{i}$ are primitive.

For any i there is a unique rectangle, denoted by $D_{i}$ , such that:

• • $\Delta _{i}$ is a right vertical subrectangle of $D_{i}$ ;

• • the interior of $D_{i}$ is disjoint from $\tilde {\mathcal Y}$ ;

• • $D_{i}$ contains a point of $\tilde {\mathcal Y}$ on its left unstable side $\partial ^{u,\mathrm {left}}D_{i}$ .

In other words, starting with $\Delta _{i}$ , we push its left unstable side to the left until we find a point in $\tilde {\mathcal Y}$ for the first time.

Claim 2. There are $1<c<C$ such that for every i,

$$ \begin{align*}c<\frac{\ell^{s}(D_{i})}{\ell^{s}(\Delta_{i})} <C.\end{align*} $$

Proof. There are finitely many orbits of primitive ${\mathcal X}$ -rectangles and therefore there are also finitely many orbits of associated rectangles $D_{i}$ . The ratio in the statement is invariant under the action of A and of integer translations, which gives the desired result.

We denote by $x_{i}^{0}$ the origin of $\Delta _{i}$ for every $i\in {\mathbb N}$ ( $x_{0}=x_{0}^{0}$ ). By assumption all the $x_{i}^{0}$ belong to $\tilde {\mathcal X}$ .

As ${\mathcal X}$ is finite and $f_{A}$ -invariant, every point is periodic. Let $n>0$ denote a common period of all points in ${\mathcal X}$ and let $T_{z}$ be the translation by $z\in \tilde {\mathcal X}$ in ${\mathcal P}_{X_{A}}$ . By definition of n, for every $z\in \tilde {\mathcal X}$ , $\phi _{z}:=T_{z}\circ A^{n} \circ T_{z}^{-1} $ is the (unique) lift of $f_{A}^{n}$ having z as a fixed point. $\phi _{z}$ is affine and its derivative on ${\mathbb R}^{2}$ is $A^{n}$ in the canonical coordinates. In the $F^{s}_{X},F^{u}_{X}$ coordinates, the derivative of $\phi _{z}$ is

$$ \begin{align*} \left( \begin{array}{@{}cc@{}} \lambda^{-n}&0\\ 0&\lambda^{n} \end{array} \right). \end{align*} $$

We are ready to define the rectangles $R_{i}$ of the staircase by induction, and we start by fixing $R_{0}=\Delta _{0}$ .

Assume that $R_{i}$ has been defined and denote by $x_{i+1}$ the endpoint of its increasing diagonal. Consider $g_{i}$ in the group generated by A and the integer translations such that $x_{i+1}= g_{i}(x_{i+1}^{0})$ .

Consider $g_{i}(D_{i+1})$ . This is a rectangle whose bottom stable side contains $x_{i+1}$ . We consider the orbit of $g_{i}(D_{i+1})$ by $\phi _{i+1}:=\phi _{x_{i+1}}$ , which consists of rectangles containing $x_{i+1}$ in their bottom stable side.

Claim 3. For large $k>0$ , $\phi _{i+1}^{k}(g_{i}(D_{i+1}))$ is disjoint from $F^{u}_{X}(x_{0})$ and $\phi _{i+1}^{-k}(g_{i}(D_{i+1}))$ is not disjoint from $F^{u}_{X}(x_{0})$ .

Let $k_{i+1}=\min \{k| \phi _{i+1}^{-k}(g_{i}(D_{i+1}))\cap F^{u}_{X}(x_{0})\neq \emptyset \}$ and

$$ \begin{align*}h_{i+1}=\phi_{i+1}^{-k_{i+1}}\circ g_{i}.\end{align*} $$

By construction (see Figure 17) $F^{u}_{X}(x_{0})$ cuts $h_{i+1}(D_{i+1})$ in two vertical subrectangles: $R_{i+1}$ is the right subrectangle. Notice that $R_{i+1}$ is disjoint from $\tilde {\mathcal Y}$ as it is included in the image of $D_{i}\setminus \partial ^{u,\mathrm {left}}(D_{i})$ by $h_{i+1}$ .

Figure 17 Constructing a positive ${\mathcal X}$ -staircase from a positive ${\mathcal X}$ -string. Colour available online.

This defines by induction a family of rectangles $\{R_{i}\}$ satisfying all the conditions of Definition 8.1 except possibly (4). It remains to check that ${{\ell ^{s}(R_{i+1}) }/{\ell ^{s}(R_{i})}}$ is bounded. Recall that $R_{i+1}$ is a right vertical subrectangle of $h_{i+1}(D_{i+1})$ and that $D_{i+1}$ admits $\Delta _{i+1}$ as a right vertical subrectangle. Let us denote $a_{i+1}=\ell ^{s}(\Delta _{i+1})$ and $b_{i+1}=\ell ^{s}(\widetilde \Delta _{i+1})$ , where $\widetilde \Delta _{i+1}=\overline {D_{i+1}\setminus \Delta _{i+1}}$ .

Because of the invariance of the ratio ${{a_{i}}/{b_{i}}}$ under the action of integer translations or A and thanks to the finiteness of orbits of primitive ${\mathcal X}$ -rectangles, one gets that ${{a_{i}}/{b_{i}}}$ and ${{b_{i}}/{a_{i}}}$ are bounded.

Now recall that $h_{i+1}$ is obtained by composing $g_{i}$ with $\phi ^{-k_{i+1}}_{i+1}$ , where $k_{i+1}$ is the minimal integer k for which $\phi _{i+1}^{-k}\circ g_{i}(D_{i+1})$ meets $F^{u}_{+}(x_{0})$ . This implies (see Figure 17) that

$$ \begin{align*}\sum_{j=0}^{i} \ell^{s}(h_{j}(\Delta_{j}))<\ell^{s}(h_{i+1}(\widetilde \Delta_{i+1}))<\lambda^{n}. \sum_{j=0}^{i} \ell^{s}(h_{j}(\Delta_{j})).\end{align*} $$

Let $\ell _{i}=\ell ^{s}(h_{i}(\Delta _{i}))$ and $\tilde \ell _{i}=\ell ^{s}(h_{i}(\widetilde \Delta _{i}))$ . Then ${{\ell _{i}}/{\tilde \ell _{i}}={a_{i}}/{b_{i}}}$ (because $h_{i}$ is affine), so this ratio and its inverse are bounded.

By the previous inequality we have that ${{\tilde \ell _{i+1}}/{\sum _{j=0}^{i} \ell _{j}}\in [1,\lambda ^{n}]}$ . Hence, there is $C>0$ so that ${{\ell _{i+1}}/{\sum _{j=0}^{i} \ell _{j}}\in [1/C,C]}$ . Finally, using the fact that $\ell ^{s}(R_{i})=\sum _{j=0}^{i} \ell _{j}$ , we have that ${{\ell ^{s}(R_{i+1})}/{\ell ^{s}(R_{i})}}$ is bounded from above. Therefore, $(R_{i})_{i\in \mathbb {N}}$ satisfies property (4) of the definition of a staircase and is indeed a positive ${\mathcal X}$ -staircase disjoint from $\tilde {\mathcal Y}$ .

Remark 8.4. If ${\mathcal Y}$ is a non-empty finite invariant set then for any finite invariant ${\mathcal X}$ any ${\mathcal X}$ -staircase ${\mathcal R}=\{R_{i}\}$ disjoint from $\tilde {\mathcal Y}$ has an axis of bounded length:

$$ \begin{align*}\ell({\mathcal I}^{u}({\mathcal R}))<\infty.\end{align*} $$

Indeed, if this is not the case, then $\bigcup _{i=0}^{+\infty }R_{i}$ would contain the infinite band $\partial ^{s,\mathrm {low}}R_{0} \times [0,+\infty )$ , which projects to whole torus $\mathbb {T}^{2}$ and thus contains points of $\tilde {{\mathcal Y}}$ .

Remark 8.5. Because of the previous remark, if $\Delta _{i}$ is the ${\mathcal X}$ -string associated to the ${\mathcal X}$ -staircase ${\mathcal R}=\{R_{i}\}$ (see Definition 8.1), then since the $\Delta _{i}$ are primitive ${\mathcal X}$ -rectangles (hence finite in number up to the action of $\pi _{1}(M)$ ) and $\ell ^{u}(\Delta _{i})\rightarrow 0$ , we have that $\ell ^{s}(\Delta _{i})\rightarrow +\infty $ . Therefore,

$$ \begin{align*}\ell^{s}(R_{i})\rightarrow +\infty.\end{align*} $$

8.4 Staircase and the holonomy game: proof of Lemma 8.2

In this section we give the proof of Lemma 8.2, thus completing the proof of Theorems 17 and 9. The proof will be the result of three fairly simple observations given in the form of lemmas.

Let ${\mathcal R}=\{R_{i}\}$ be a $({\mathcal X},x,+,+)$ -staircase disjoint from $\tilde {\mathcal Y}$ for some $x\in \tilde {\mathcal X}$ . For any i we denote by $R_{i,{\mathcal Y}}$ (see Figure 18) the unique rectangle with the following properties:

• • $\partial ^{u,\mathrm {left}} R_{i,{\mathcal Y}}=\partial ^{u,\mathrm {left}}R_{i}\subset F^{u}_{+}(x)$ ;

• • $R_{i,{\mathcal Y}}\cap \tilde {{\mathcal Y}}=\partial ^{u,\mathrm {right}}R_{i,{\mathcal Y}}\cap \tilde {{\mathcal Y}}\neq \emptyset $ .

In other words, one pushes the right side of $R_{i}$ to the right until it intersects $\tilde {{\mathcal Y}}$ for the first time.

Figure 18 In the above picture red (respectively, blue ) points represent points in $\tilde {\mathcal Y}$ (respectively, $\tilde {\mathcal X}$ ), white rectangles represent the staircase ${\mathcal R}_{i}$ and the blue (grey) rectangles the safety zones $S_{i}$ . Colour available online.

We denote $S_{i,{\mathcal Y}}=\overline {R_{i,{\mathcal Y}}\setminus R_{i}}$ . This is a right vertical subrectangle of $R_{i,{\mathcal Y}}$ called the ${\mathcal Y}$ -safe zone of $R_{i}$ . We also denote by $(\Delta _{i})_{i\in \mathbb {N}}$ the ${\mathcal X}$ -string of rectangles associated to the ${\mathcal X}$ -staircase ${\mathcal R}$ (see Definition 8.1).

Once again, because of the finiteness of the number of orbits of ${\mathcal X}$ -rectangles, one gets that the ratio ${{\ell ^{s}(S_{i,{\mathcal Y}})}/{\ell ^{s}(\Delta _{i})}}$ takes a finite number of values (in particular, this ratio and its inverse are bounded).

For any i, let

$$ \begin{align*}q_{i}=\partial^{s,\mathrm{low}}R_{i}\cap F^{u}_{+}(x) \quad\mbox{and}\quad q=\lim q_{i}\in F^{u}_{+}(x).\end{align*} $$

Let us note here that $q< \infty $ , because of Remark 8.4.

For any $Y\in {\mathcal S} urg(A,{\mathcal X},{\mathcal Y})$ we denote by $h_{i,Y}\colon F^{s}_{+}(q_{i})\to F^{s}_{+}(q_{i+1})$ the holonomy of $F^{u}_{Y}$ .

Lemma 8.3. Using the above notation, we have:

• • if $(t,q_{i})\in \partial ^{s,\mathrm {low}}(R_{i})$ then

  $$ \begin{align*}h_{i,Y}(t,q_{i})=(t,q_{i+1});\end{align*} $$

• • if $(t,q_{i})\in \partial ^{s,\mathrm {low}}(S_{i,{\mathcal Y}})$ then

  $$ \begin{align*}h_{i,Y}(t,q_{i})=(t_{i+1}+ \lambda^{-\tau(x_{i+1})}(t-t_{i+1}),q_{i+1}),\end{align*} $$
  where $x_{i+1}=(t_{i+1},q_{i+1})=\partial ^{s,\mathrm {low}}(R_{i+1})\cap \tilde {\mathcal X}$ and $\tau (x_{i+1})=m(x_{i+1})\cdot \pi (x_{i+1})$ is the twist number associated to $x_{i+1}$ , in which $m(x_{i+1})$ is the characteristic number of the surgery at the orbit corresponding to $x_{i+1}$ and $\pi (x_{i+1})$ is its period.

Proof. Just notice that for points in $\partial ^{s,\mathrm {low}}(R_{i})$ their positive unstable leaf reaches $F^{s}_{+}(q_{i+1})$ without crossing any positive stable leaf of a point in $\tilde {\mathcal X}\cup \tilde {\mathcal Y}$ at the right of $F^{u}(x)$ , so the holonomy is not affected by the surgeries. For the points in $\partial ^{s,\mathrm {low}}(S_{i,{\mathcal Y}})$ , the unique moment when they cross a positive stable leaf of a point in $\tilde {\mathcal X}\cup \tilde {\mathcal Y}$ at the right of $F^{u}(x)$ is precisely when they reach $F^{s}_{+}(q_{i+1})$ : they cross the positive stable leaf of $x_{i+1}$ , leading to the claimed formula.

Lemma 8.4. If for every i we have

$$ \begin{align*}\partial^{s,\mathrm{low}}(R_{i+1,{\mathcal Y}})\subset h_{i,Y}(\partial^{s,\mathrm{low}}(R_{i,{\mathcal Y}}))\end{align*} $$

then $C_{+,+}(x)$ is undertwisted.

Proof. In this case the image by the holonomy of $F^{u}_{Y}$ of $\partial ^{s,\mathrm {low}}(R_{0,{\mathcal Y}})$ on $F^{s}_{+}(q_{i})$ contains the segment $\partial ^{s,\mathrm {low}}(R_{i,{\mathcal Y}})$ whose length tends to infinity, thanks to Remark 8.5. Thus the holonomy from $F^{s}_{+}(x)$ to $F^{s}_{+}(q)$ takes $\partial ^{s,\mathrm {low}}(R_{0,{\mathcal Y}})$ to the whole of $F^{s}_{+}(q)$ , so the domain of that holonomy is contained in $\partial ^{s,\mathrm {low}}(R_{0,{\mathcal Y}})$ , which finishes the proof.

Recall that the ratios ${{\ell ^{s}(\Delta _{i+1})}/{\ell ^{s}(\Delta _{i})}}$ , ${{\ell ^{s}(S_{i+1})}/{\ell ^{s}(\Delta _{i+1})}}$ , ${{\ell ^{s}(\Delta _{i})}/{\ell ^{s}(S_{i})}}$ are bounded, therefore there is $C>0$ such that for every i,

$$ \begin{align*}\frac{\ell^{s}(\Delta_{i+1})+\ell^{s}(S_{i+1})}{\ell^{s}(S_{i})}<C.\end{align*} $$

Lemma 8.5. For all $x\in {\mathcal X}$ , let $m(x)$ be the characteristic number of the surgery associated to x. Assume that all the $m(x)$ are negative and of large absolute value, so that the product $\tau (x)=m(x)\pi (x)$ (where $\pi $ is the period function) satisfies, for every $x\in {\mathcal X}$ ,

$$ \begin{align*}\lambda^{|\tau(x)|}>C.\end{align*} $$

Then for every i, one gets $\partial ^{s,\mathrm {low}}(R_{i+1,{\mathcal Y}})\subset h_{i,Y}(\partial ^{s,\mathrm {low}}(R_{i,{\mathcal Y}}))$ , and by the previous lemma $C_{+,+}(x)$ is incomplete.

An example of a holonomy game that satisfies the hypotheses of the previous lemma is given in Figure 18. By combining the three previous lemmas, we obtain the proof of Lemma 8.2.

8.5 Abundance of pairs $({\mathcal X},{\mathcal Y})$ with strings of rectangles

As the proof of Theorem 9 has reached its end, we continue by proving Theorem 16, as promised at the beginning of §7. In fact, in this section we prove in Corollary 8.1 a much stronger result, closely resembling Theorem 6. Notice that Theorem 16 is a straightforward consequence of Corollary 8.1 applied for ${\mathcal E}=\emptyset $ .

Consider two distinct periodic orbits ${\mathcal X}$ and ${\mathcal Y}$ and the points $x\in \tilde {\mathcal X}$ and $y\in \tilde {\mathcal Y}$ . We recall that, thanks to Remark 8.1, if there is a positive ${\mathcal X}$ -rectangle R disjoint from $\tilde {\mathcal Y}$ , then there is a positive ${\mathcal X}$ -string disjoint from $\tilde {\mathcal Y}$ based at x.

In order to prove the next corollary, we will use the following classical fact from ergodic theory.

Lemma 8.6. Let f be a diffeomorphism of a compact surface, p a hyperbolic periodic saddle point and $q_{1},\ldots ,q_{k}$ transverse homoclinic intersections between a stable separatrix in $W^{s}(Orb(p))$ and an unstable separatrix in $W^{u}(Orb(p))$ . Denote by K the union of the orbit of p and of the orbits of the $q_{i}$ , which is an invariant compact set. Then for any neighbourhood U of K, there is a hyperbolic basic set $\Lambda _{U}$ (that is, transitive and with local product structure) satisfying $K \subsetneq \Lambda _{U} \subsetneq U$

We are ready to prove the main result of this section.

Lemma 8.7. Let $B\in SL(2,{\mathbb Z})$ be a hyperbolic matrix (possibly with negative eigenvalues). Let ${\mathcal E}\subset {\mathbb T}^{2}$ be a finite $f_{B}$ -invariant set. Then there are periodic orbits $\gamma _{+}$ , $\gamma _{-}$ such that there exist positive and negative $\gamma _{+}$ -rectangles (respectively, $\gamma _{-}$ -rectangles) disjoint from $\gamma _{-}\cup {\mathcal E}$ (respectively, $\gamma _{+}\cup {\mathcal E}$ ). Furthermore, if B has negative eigenvalues, one can choose $\gamma _{+}$ , $\gamma _{-}$ each with an arbitrary sign of eigenvalues, for instance negative.

Proof. Choose two distinct periodic points $\sigma _{+} \notin {\mathcal E}$ and $\sigma _{-} \notin {\mathcal E}$ . If B has negative eigenvalues, one can choose $\sigma +$ and $\sigma _{-}$ with negative eigenvalues (that is, with odd periods). For each orbit $\sigma _{\pm }$ we choose $q_{i,\pm }$ , $i=1,\ldots , 4$ , four homoclinic intersections between the two stable and the two unstable separatrices of $\sigma _{\pm }$ . We denote by $K_{\pm }$ the compact obtained by the union of $\sigma _{\pm }$ and the orbits of the $q_{i,\pm }$ .

We choose neighbourhoods $U_{\pm }$ of $K_{\pm }$ such that $U_{+}\cap U_{-}=U_{+}\cap {\mathcal E}= U_{-}\cap {\mathcal E}= \emptyset $ . We denote by $\Lambda _{\pm }$ the hyperbolic basic sets contained in $U_{\pm }$ and containing $K_{\pm }$ given by Lemma 8.6.

There is $\varepsilon>0$ such that every periodic orbit $\gamma _{+}$ in $\Lambda _{+}$ which is $\varepsilon $ -dense in $\Lambda _{+}$ admits positive and negative $\gamma _{+}$ -rectangles disjoint from ${\mathcal E}$ and from $\Lambda _{-}$ .

In the same way, for $\varepsilon>0$ small enough, any periodic orbit $\gamma _{-}\subset \Lambda _{-}$ , which is $\varepsilon $ -dense admits positive and negative rectangles disjoint from ${\mathcal E}$ and from $\Lambda _{+}$ .

We conclude the proof of Lemma 8.7 with the following claim.

Claim 4. If B has negative eigenvalues, each of the basic sets $\Lambda _{\pm }$ contains the periodic orbit $\sigma _{\pm }$ with negative eigenvalues and therefore admits $\varepsilon $ -dense orbits with negative eigenvalues.

Proof. The basic sets $\Lambda _{\pm }$ admit Markov partitions. A $\varepsilon $ -dense periodic orbit $\gamma _{0}$ , for small $\varepsilon $ , contains the code of $\sigma _{\pm }$ for this Markov partition and this code is a word of odd length. We get a new $\varepsilon $ -dense orbit $\gamma _{1}$ by repeating once more the code of $\sigma _{\pm }$ in the one of $\gamma _{0}$ . Now, either $\gamma _{0}$ or $\gamma _{1}$ has odd period, which concludes the proof of the claim.

As a result of Theorem 17 and Lemma 8.7 we obtain the following corollary.

Corollary 8.1. Let $A\in SL(2,{\mathbb Z})$ be a matrix with positive eigenvalues and ${\mathcal E}$ be a finite $f_{A}$ -invariant set. Let $\gamma _{+}$ and $\gamma _{-}$ be the periodic orbits obtained by Lemma 8.7. There exists $n>0$ such that every flow Y obtained from $X_{A}$ by surgeries along ${\mathcal E}$ and by two surgeries of distinct signs along $\gamma _{+}$ and $\gamma _{-}$ with characteristic numbers of absolute value greater than n is not ${\mathbb R}$ -covered.

Proof. By Remark 8.1 and using the notation of the proof of Lemma 8.7, there exist positive and negative $\gamma _{+}$ -strings (respectively, $\gamma _{-}$ -strings) disjoint from ${\mathcal E}\cup \Lambda _{-}$ (respectively, ${\mathcal E}\cup \Lambda _{+}$ ).

Then Theorem 17 implies that large negative surgeries along $\gamma _{+}$ induce incomplete $C_{+,+}$ quadrants (at any point of the bifoliated plane associated to $\gamma _{+}$ ) independently of the surgeries we perform on $\gamma _{-}\cup {\mathcal E}$ . In the same way large positive surgeries along $\gamma _{-}$ induce incomplete $C_{+,-}$ quadrants at any point associated to $\gamma _{-}$ .

Therefore, by performing large positive surgeries along $\gamma _{-}$ and large negative surgeries along $\gamma _{+}$ one obtains a non- ${\mathbb R}$ -covered flow Y, independently of the surgeries performed along ${\mathcal E}$ .

In order to prove Theorems 5 and 6, we would like to remove the ‘large enough’ hypothesis in Corollary 8.1.

8.6 Replacing large characteristic numbers by large periods

The aim of this section is to go from the proof of Theorems 17 and 9 to the proof of Theorems 5 and 6. As Theorem 6 clearly implies Theorem 5, we will only prove Theorem 6, that is, for any finite set ${\mathcal E}$ of periodic orbits there exist two periodic orbits $\gamma _{+}$ and $\gamma _{-}$ such that any $Y\in {\mathcal S} urg(X_{A},{\mathcal E}\cup \gamma _{+}\cup \gamma _{-})$ for which the surgeries along $\gamma _{+}$ and $\gamma _{-}$ are of different signs is not ${\mathbb R}$ -covered.

8.6.1 Choosing a staircase and a safety zone

As in the proof of Lemma 8.7, we first build two disjoint hyperbolic basic sets $\Lambda _{+}$ and $\Lambda _{-}$ in ${\mathbb T}^{2}$ that do not intersect ${\mathcal E}$ . Then, for $\varepsilon _{0}>0$ sufficiently small, any $\varepsilon _{0}$ -dense (in $\Lambda _{\pm }$ ) periodic orbit $\sigma _{\pm }\subset \Lambda _{\pm }$ admits a positive and a negative $\sigma _{\pm }$ -string disjoint from $\tilde {\mathcal E} \cup \tilde \Lambda _{\mp }$ .

Remark 8.6. A classical fact in hyperbolic dynamical systems on surfaces is that hyperbolic basic sets $\Lambda $ admit at most finitely many periodic boundary points (see, for instance, [BoLa2]), that is, points which are not accumulated by points in $\Lambda $ in each of their four quadrants.

Therefore, if $\varepsilon _{0}$ is taken very small, the orbits $\sigma _{+}$ and $\sigma _{-}$ are not boundary periodic points of $\Lambda _{+}$ and $\Lambda _{-}$ , respectively.

From this point on, we will concentrate on $\sigma _{+}$ ; the results stated for $\sigma _{+}$ can be proven in the exact same way for $\sigma _{-}$ . Because of the previous remark and thanks to Lemma 8.1, one can build in each quadrant $C_{\pm \pm }(\sigma _{+})$ positive or negative (according to the quadrant) staircases for $\sigma _{+}$ disjoint from $\tilde {\mathcal E} \cup \tilde \Lambda _{-}$ .

Fix $x\in \tilde {\sigma }_{+}$ , where $\tilde {\sigma }_{+}$ is the lift of $\sigma _{+}$ in the bifoliated plane. For the sake of simplicity, we will restrict ourselves from now on to the $(+,+)$ quadrant of x; the proofs of all the following results can be adapted for all the other quadrants of x.

Consider in $C_{+,+}(x)$ a $\sigma _{+}$ -staircase $\{R_{i}\}$ disjoint from $\tilde {\mathcal E} \cup \tilde \Lambda _{-}$ based at x, its associated positive $\sigma _{+}$ -string $\{\Delta _{i}\}$ (see Definition 8.1) and its extension by its ${\mathcal E}\cup \Lambda _{-}$ -safe zone $S_{i}:=S_{i,{\mathcal E}\cup \Lambda _{-}}$ (see §8.4 for the definition of the ${\mathcal Y}$ -safe zone $S_{i,{\mathcal Y}}$ , where ${\mathcal Y}={\mathcal E}\cup \Lambda _{-}$ ).

We recall that (see Figure 19):

• • ${\mathcal R}=\{R_{i}\}$ are the rectangles of a staircase disjoint from ${\mathcal E}\cup \Lambda _{-}$ . Their left unstable sides are adjacent segments on $F^{u}_{+}(x)$ , whose union is a bounded interval ${\mathcal I}^{u}({\mathcal R})$ . We will denote $q_{i}=F^{u}_{+}(x)\cap \partial ^{s,\mathrm {low}}R_{i}$ . The ratio ${{\ell ^{s}(R_{i+1})}/{\ell ^{s}(R_{i})}}$ is bounded and bounded away from $1$ .

• • $(\Delta _{i})$ is a positive $\sigma _{+}$ -string with origin at x. The $\Delta _{i}$ are right vertical subrectangles of the $R_{i}$ and the ratios ${{\ell ^{s}(R_{i})}/{\ell ^{s}(\Delta _{i})}}$ , ${{\ell ^{s}(\Delta _{i+1})}/{\ell ^{s}(\Delta _{i})}}$ and their inverses are bounded. Once again we may assume that the $\Delta _{i}$ are primitive $\sigma _{+}$ -rectangles

• • the left unstable side of the rectangles $S_{i}$ is the right stable side of the $R_{i}$ and $\Delta _{i}$ . Their intersection with ${\mathcal E}\cup \Lambda _{-}$ is contained in their right side, and finally the ratio ${{\ell ^{s}(R_{i})}/{\ell ^{s}(S_{i})}}$ is bounded with bounded inverse.

Figure 19 The rectangle $\Delta_{i,2\rho}$ in the safety zone $S_i$ . Colour available online.

8.6.2 Choosing the periodic orbits $\gamma _{+}$ and $\gamma _{-}$

Note that $\partial ^{s,\mathrm {low}}(\Delta _{i+1})$ and $\partial ^{s,\mathrm {up}}(S_{i})$ are two segments in the same stable leaf $F^{s}_{+}(q_{i+1})$ that are adjacent to the same segment $\partial ^{s,\mathrm {up}}(\Delta _{i})$ .

Furthermore, their lengths have a bounded ratio ${{\ell ^{s}(\Delta _{i+1})}/{\ell ^{s}(S_{i})}}$ .

For every i and every $\rho \in (0,1)$ we define by $J_{i+1,\rho }\subset \partial ^{s,low}(\Delta _{i+1})$ the segment adjacent from the right to $\partial ^{s,\mathrm {up}}(\Delta _{i})$ of length

$$ \begin{align*}\ell^{s}(J_{i+1,\rho})=\rho\cdot\ell^{s}(\Delta_{i+1}).\end{align*} $$

Then there is $0<\rho <1$ small enough with the following property:

$$ \begin{align*}J_{i+1,2\rho}\subset \partial^{s,\mathrm{up}}(S_{i}) \quad\text{for all }i.\end{align*} $$

Let $\Delta _{i,\rho }$ denote the left vertical subrectangle of $S_{i}$ , whose bottom stable side is $J_{i,\rho }$ (see Figure 19).

Claim 5. For any $n>0$ , there exists $\varepsilon _{n}>0$ such that any $f_{A}$ periodic orbit $\gamma _{+}\subset \Lambda _{+}$ which is $\varepsilon _{n}$ -dense (in $\Lambda _{+}$ ), has period greater than n and has more than n points in $\Delta _{i,\rho }$ for any i.

Proof. Fix $n\in \mathbb {N}$ . Take $\gamma _{+}$ a $\varepsilon $ -dense periodic orbit in $\Lambda _{+}$ and $\tilde {\gamma }_{+}$ its lift on the bifoliated plane. Up to the action of the group generated by A and the integer translations, we just need to check the claim on finitely many primitive $\sigma _{+}$ -rectangles. Thanks to Remark 8.6, we asked that $\sigma _{+}$ be accumulated by points in $\Lambda _{+}$ in each quadrant, so the interior of $\Delta _{i,\rho }$ intersects $\Lambda _{+}$ . The $\varepsilon $ -density implies that for a sufficiently small $\varepsilon $ the period of $\gamma _{+}$ is greater than n and also that $\Delta _{i,\rho }$ contains more than n points of $\tilde \gamma _{+}$ .

Using the above notation and hypotheses, the aim of this section is to prove the following proposition.

Proposition 8.1. If $n>0$ is large enough then for any vector field $Y \in {\mathcal S} urg(X,{\mathcal E}\cup \Lambda _{+}\cup \Lambda _{-})$ for which the characteristic numbers of the surgeries along $\Lambda _{+}$ are non-positive and non-zero along $\gamma _{+}$ , where $\gamma _{+}$ is $\varepsilon _{n}$ -dense in $\Lambda _{+}$ , the quadrant $C_{+,+}(x)$ is incomplete (undertwisted).

Notice that (for the first time in this paper) we perform a surgery on a periodic orbit $\gamma _{+}$ and we calculate the holonomy on a quadrant of a different periodic point.

Proof of Proposition 8.1

Proposition 8.1 is a direct consequence of the next lemma.

Lemma 8.8. Following the above notation, let $t_{i}$ be the right endpoint of $J_{i,2\rho }$ . If $n>0$ is chosen large enough then the unstable holonomy $h^{u}_{Y,q_{i},q_{i+1}}\colon F^{s}_{+}(q_{i})\to F^{s}_{i}(q_{i+1})$ satisfies one of the following assertions:

• • $h^{u}_{Y,q_{i},q_{i+1}}(t_{i})$ is not defined (so $C_{+,+}(x)$ is incomplete);

• • $t_{i+1}\in [q_{i+1},h^{u}_{Y,q_{i},q_{i+1}}(t_{i})]^{s}$ .

Proposition 8.1 follows because the length of $[q_{i},t_{i}]^{s}$ tends to infinity as $i\to \infty $ , hence the unstable holonomy from $F^{s}_{+}(x)$ to $F^{s}_{+}(q)$ (where $q=\lim q_{i}$ is the endpoint of ${\mathcal I}^{s}({\mathcal R})$ ) is not defined at $t_{0}$ .

We proceed to the proof of Lemma 8.8. Consider the holonomy game for $t_{i}$ in $R_{i} \cup S_{i}$ . Let us follow the positive unstable leaf $F^{u}_{+}(t_{i})$ . As the rectangle $R_{i} \cup S_{i}$ is disjoint from $\tilde {\mathcal E}\cup \tilde \Lambda _{-}$ and as the surgeries along periodic orbits in $\Lambda _{+}$ have non-negative characteristic numbers, all holonomies are expansions as long as the point remains inside $R_{i}\cup S_{i}$ .

If, while following the holonomy, we exit $R_{i}\cup S_{i}$ before reaching $F^{s}_{+}(q_{i+1})$ , it is impossible to go back in later in the game. Consequently, either the holonomy $h^{u}_{Y,q_{i},q_{i+1}}$ is not defined at $t_{i}$ or $t_{i+1}\in [q_{i+1},h^{u}_{Y,q_{i},q_{i+1}}(t_{i})]$ .

Therefore, we just need to check that the point $t_{i}$ exits $R_{i}\cup S_{i}$ before reaching $F^{s}_{+}(q_{i+1})$ . As all the holonomies that affect it inside $R_{i}\cup S_{i}$ are all expansions, it is enough to prove that $t_{i}$ exits $R_{i}\cup S_{i}$ before reaching $F^{s}_{+}(q_{i+1})$ only thanks to the points in $\gamma _{+}\cap \Delta _{i,\rho }$ . Each time the unstable manifold of $t_{i}$ crosses the stable manifold of one of these points, the distance to this point is multiplied by a factor larger than $\lambda ^{n}$ . This distance is at least $\rho \ell ^{s}(\Delta _{i})$ , which is in bounded ratio with $\ell ^{s}(R_{i})+\ell ^{s}(S_{i})$ .

In order to get the desired property, it is enough to choose n such that for every i, we have

$$ \begin{align*}\lambda^{n}>\frac{\ell^{s}(R_{i})+\ell^{s}(S_{i})}{\rho\ell^{s}(\Delta_{i})},\end{align*} $$

which concludes the proof of the lemma and hence of Proposition 8.1.

The previous results can be proven in the exact same way for $C_{-,-}(x)$ . Also, the same result holds for the quadrants $C_{+,-}(x^{\prime })$ , $C_{-,+}(x^{\prime })$ for any $x^{\prime } \in \tilde {\sigma }_{-}$ , when performing non-negative surgeries on $\Lambda _{-}$ and non-zero surgeries along $\gamma _{-}$ .

8.6.3 Concluding the proof of Theorem 6

Now the proof of Theorem 6 just involves applying Proposition 8.1 in the quadrants $C_{+,+} (x_{+})$ and $C_{+,-}(x_{-})$ , where $x_{+}\in \tilde {\sigma }_{+}$ and $x_{-}\in \tilde {\sigma }_{-}$ for a common choice of a small $\varepsilon $ and of orbits $\gamma _{+}\subset \Lambda _{+}$ and $\gamma _{-}\subset \Lambda _{-}$ , which are $\varepsilon $ -dense in $\Lambda _{+}$ and $\Lambda _{-}$ , respectively.

Remark 8.7. Theorem 6 only proclaims the existence of a pair of orbits $\gamma _{+}$ and $\gamma _{-}$ . In the previous proof, we have established slightly more, that is, for any two disjoint basic sets $\Lambda _{+}$ and $\Lambda _{-}$ , which are also disjoint from the arbitrary given set ${\mathcal E}$ , there is $\epsilon>0$ such that Theorem 6 holds for any $\gamma _{+}\subset \Lambda _{+}$ and $\gamma _{-}\subset \Lambda _{-}$ which are $\varepsilon $ -dense in $\Lambda _{+}$ and $\Lambda _{-}$ , respectively.

8.7 The case of matrices with negative eigenvalues

In this section we consider a hyperbolic matrix $B\in SL(2,{\mathbb Z})$ with negative eigenvalues, and $X_{B}$ is the suspension flow of $f_{B}$ on the manifold $M_{B}$ , the mapping torus of $f_{B}$ . We let $A=B^{2}$ and denote by $X_{A}$ the suspension flow of $f_{A}$ on $M_{A}$ . The matrix A is hyperbolic with positive eigenvalues and $M_{A}$ is the $2$ -fold cover of the orientations of the stable/unstable bundles of $X_{B}$ . The Anosov flow $X_{A}$ is the lift of $X_{B}$ on $M_{A}$ .

We start by proving Theorem 9 for matrices with negative eigenvalues. Let ${\mathcal X},{\mathcal Y}$ be two disjoint finite $f_{B}$ -invariant sets. Assume that for every $x\in {\mathcal X}$ there exists a positive ${\mathcal X}$ -rectangle with origin x disjoint from $\tilde {{\mathcal Y}}$ and for every $y\in {\mathcal Y}$ a negative ${\mathcal Y}$ -rectangle with origin y disjoint from $ \tilde {{\mathcal X}}$ .

Let ${\mathcal X}_{A}$ , ${\mathcal Y}_{A}$ be the lifts on $M_{A}$ of ${\mathcal X}$ , ${\mathcal Y}$ , respectively. We can identify the bifoliated plane of $X_{A}$ and $X_{B}$ , and under this identification the lifts of ${\mathcal X}_{A}$ , ${\mathcal Y}_{A}$ on ${\mathcal P}_{X_{A}}={\mathcal P}_{X_{B}}$ coincide with the lifts $\tilde {\mathcal X}$ , $\tilde {\mathcal Y}$ of ${\mathcal X}$ and ${\mathcal Y}$ .

So, for every $x\in \tilde {\mathcal X}$ there exists a positive ${\mathcal X}_{A}$ -rectangle with origin x disjoint from $ \tilde {{\mathcal Y}}$ , and for every $y\in \tilde {\mathcal Y}$ a negative ${\mathcal Y}_{A}$ -rectangle with origin y disjoint from $ \tilde {{\mathcal X}}$ . Thus one may apply Theorem 9 to $X_{A}, {\mathcal X}_{A},{\mathcal Y}_{A}$ : there is $N>0$ such that every Anosov flow of the form ${{\mathcal S}}urg(X_{A},{\mathcal X}_{A},{\mathcal Y}_{A},(m_{i})_{i\in I}, (n_{j})_{j\in J})$ with $m_{i}\leq -N$ and $n_{j}\geq N$ is not ${\mathbb R}$ -covered.

In order to prove Theorem 9 for matrices with negative eigenvalues it suffices to notice that any flow Y, obtained by surgery on $X_{B}$ along ${\mathcal X}$ , ${\mathcal Y}$ , negative on ${\mathcal X}$ and positive on ${\mathcal Y}$ and larger than N in absolute value, lifts on $M_{A}$ to a flow $Y_{A}$ obtained by a surgery on $X_{A}$ along ${\mathcal X}_{A}$ , ${\mathcal Y}_{A}$ , negative on ${\mathcal X}_{A}$ and positive on ${\mathcal Y}_{A}$ and larger than N in absolute value (see Remark 4.1). Therefore $Y_{A}$ is non- ${\mathbb R}$ -covered and so is Y.

We will now prove Theorem 6 (and thus Theorem 5) for the above matrix B with negative eigenvalues. Consider a finite $f_{B}$ -invariant set ${\mathcal E}$ . Lemma 8.7 provides two basic sets $\Lambda _{+}$ and $\Lambda _{-}$ disjoint from each other and from ${\mathcal E}$ and two periodic orbits with negative eigenvalues $\gamma _{+}\subset \Lambda _{+}$ and $\gamma _{-}\subset \Lambda _{-}$ , which are $\varepsilon $ -dense in $\Lambda _{+}$ and $\Lambda _{-}$ , respectively, for any $\varepsilon>0$ .

Let ${\mathcal E}_{A}$ , $\Lambda _{+,A}$ and $\Lambda _{-,A}$ be the lifts on $M_{A}$ of ${\mathcal E}$ , $\Lambda _{+}$ and $\Lambda _{-}$ , respectively. In the same way, for any $\varepsilon>0$ , we denote by $\gamma _{+,A}$ and $\gamma _{-,A}$ the lifts on $M_{A}$ of $\gamma _{+}$ and $\gamma _{-}$ , respectively. As $\gamma _{+}$ and $\gamma _{-}$ have negative eigenvalues, one gets that each of $\gamma _{+,A}$ and $\gamma _{-,A}$ is a (unique) periodic orbit. Notice that $\Lambda _{\pm ,A}$ is still a basic set: the issue is that its lift could be the union of two disjoint basic sets (thus breaking the transitivity) which is avoided in this case since $\gamma _{\pm ,A}$ is a unique orbit. Note that $\gamma _{\pm ,A}$ is $\varepsilon $ -dense in $\Lambda _{\pm ,A}$

We now conclude the proof of Theorem 6 as in the case of matrices with positive eigenvalues, by applying Proposition 8.1 for the flow $X_{A}$ , the finite $f_{A}$ -invariant set ${\mathcal E}_{A}$ , the two basic sets $\Lambda _{\pm ,A}$ and $\gamma _{\pm ,A}$ , where $\gamma _{\pm }$ is $\varepsilon _{n}$ dense in $\Lambda _{\pm }$ , for n large enough.

9 Surgeries along two periodic orbits

The aim of this section is to give an overview of the vector fields obtained from a suspension flow $X_{A}$ , where $A \in SL(2,{\mathbb Z})$ , by performing surgeries along exactly two periodic orbits. In other words, using the previous notation, ${\mathcal X}$ and ${\mathcal Y}$ are each a single periodic orbit.

There are, in theory, $16$ different cases, according to the existence or non-existence of positive or negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ or ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ (see Figure 20). We denote by $(\checkmark , \times )$ the existence of positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and the non-existence of negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ . We define similarly the symbols $(\checkmark , \checkmark ), (\times ,\checkmark )$ and $(\times ,\times )$ . We use the same notation for ${\mathcal Y}$ -rectangles.

Figure 20 In this figure, crossed rectangles correspond to impossible cases, green (grey) rectangles correspond to cases that we consider and white rectangles to cases that are similar to a case that we consider up to symmetry. Colour available online.

Lemma 2.3 implies that if there are no positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ then there are negative ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ . Therefore, seven of the above 16 cases are impossible (see Figure 20).

Also, up to interchanging ${\mathcal Y}$ and ${\mathcal X}$ , we can restrict ourselves to the upper triangular part of Figure 20 and, up to interchanging positive and negative, we can furthermore restrict ourselves to the following four cases among the cases in the upper triangular part.

1. (1) There are positive and negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ .

2. (2) There are no ${\mathcal X}$ -rectangles (either positive or negative) disjoint from $\tilde {\mathcal Y}$ (so there are positive and negative ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ ).

3. (3) There are no negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and no negative ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ (thus according to Lemma 2.3 there are positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and positive ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ ).

4. (4) There are no positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ , but there are rectangles in the three other categories.

In each case we will consider the vector field $Z_{m,n}$ obtained by an $(m,n)$ surgery along ${\mathcal X}$ and ${\mathcal Y}$ and discuss what we know about the bifoliated plane of $Z_{m,n}$ , according to the position of $(m,n)$ in the lattice ${\mathbb Z}^{2}$ ; see Figure 22.

Recall that, according to [Fe1], if $n,m$ have the same sign (or one of them vanishes) then $Z_{m,n}$ is ${\mathbb R}$ -covered twisted in the direction of that sign. We will therefore only consider the case where $m\cdot n<0$ .

9.1 Case 1: existence of positive/negative ${\mathcal X}$ , ${\mathcal Y}$ -rectangles disjoint from ${\mathcal Y}$ , ${\mathcal X}$

This case can be realized by considering periodic points in the neighbourhood of the homoclinic intersections of any two fixed (a priori) periodic points, as already done in the proof of Lemma 8.7. In this case:

• • if $n,m$ have opposite signs and are large enough, then $Z_{m,n}$ is not ${\mathbb R}$ -covered according to Theorem 9;

• • if $n,m$ have opposite signs and one of them is large enough, then, using Lemma 8.1, some quadrant is incomplete and $Z_{n,m}$ is not a suspension flow.

9.2 Case 2: no ${\mathcal X}$ -rectangle disjoint from $\tilde {\mathcal Y}$

This case can be realized as follows: take any ${\mathcal X}\subset {\mathbb T}^{2}$ and choose $\varepsilon>0$ small enough such that any $\varepsilon $ -dense periodic orbit ${\mathcal Y}$ intersects the interior of every ${\mathcal X}$ -rectangle. In this case,

• • if n is large enough in absolute value then, using Theorem 8, $Z_{m,n}$ is ${\mathbb R}$ -covered twisted in the direction of the sign of n.

9.3 Case 3: no negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and no negative ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$

In contrast to the previous cases, we are not aware of a large family of examples in which this case is realized. Nevertheless, one could check that if ${\mathcal X}=(0,0)$ , ${\mathcal Y}=(0,1/2)$ and

$$ \begin{align*}A=\left(\begin{array}{@{}cc@{}} 3&2\\ 4&3 \end{array}\right)\end{align*} $$

(see Figure 21) there are no negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ and no negative ${\mathcal Y}$ -rectangles disjoint from $\tilde {\mathcal X}$ . Our proof of this fact involves understanding the nature of the continued fractions associated to the slopes of the eigendirections and thus goes beyond the purposes of this paper. In this case,

• • if n or m is negative and large enough in absolute value then, using Theorem 8, $Z_{m,n}$ is ${\mathbb R}$ -covered negatively twisted.

Figure 21 In this figure red points ( ) represent lifts of the point $(0,\tfrac 12)$ , blue points ( ) lifts of $(0,0)$ , the red (black) line is the stable eigendirection and the green (grey) one the unstable. An ${\mathcal X}$ -rectangle disjoint from $\tilde {\mathcal Y}$ is traced; we can see that there are no negative ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ . Colour available online.

9.4 Case 4: no positive ${\mathcal X}$ -rectangles disjoint from $\tilde {\mathcal Y}$ , but existence of all other rectangles

We have not been able to come up with an example satisfying the hypotheses of this case, but it seems possible to us that an example similar to that of case 3 also makes this case realizable. In this case:

• • if n is positive and large enough, then using Theorem 8, $Z_{m,n}$ is ${\mathbb R}$ -covered positively twisted;

• • if m is positive and large enough and n is negative and large enough in absolute value, then, using Theorem 9, $Z_{m,n}$ is non- ${\mathbb R}$ -covered.

Remark 9.1. As we have seen above, for any hyperbolic matrix with positive eigenvalues in $SL(2,\mathbb {Z})$ , we can reproduce cases 1 and 2 by choosing in an appropriate way a pair of periodic orbits. We are not able to reproduce the cases 3 and 4 in a similar way. Indeed, we think that for most matrices, there are no pairs of periodic orbits that satisfy those hypotheses.

Remark 9.2. In each of the above cases, keeping in mind Fenley’s theorem, the set of points in $\mathbb {Z}^{2}$ for which we do not know the outcome of the corresponding surgeries is either finite or the union of vertical/horizontal half bands of the form $[\![ k, l ]\!] \times \mathbb {Z}^{+,-}$ or $\mathbb {Z}^{+,-} \times [\![ k, l ]\!] $ , where $k,l \in \mathbb {Z}$ (see Figure 22).

Figure 22 The horizontal axis in each case in this figure is the m-axis and the vertical one the n-axis.

Lemma 9.1. For any band B of the form $\mathbb {Z}\times [\![ k, l ]\!]$ , where $k,l \in \mathbb {Z}$ , there are finitely many $(m,n)\in B$ such that $Z_{m,n}$ is a suspension flow.

Proof. Indeed, suppose that $Z_{m_{0},n_{0}}$ is a suspension flow. According to [Fe1], for every $m\in \mathbb {Z}-\{m_{0}\} Z_{m,n_{0}}$ is a twisted $\mathbb {R}$ -covered flow. We deduce that there are at most $l-k$ suspension Anosov flows in B.

As a direct consequence of Remark 9.2 and Lemma 9.1 we obtain the following proposition.

Proposition 9.1. For every $A \in SL_{2}(\mathbb {Z})$ and $\gamma _{+}, \gamma _{-}$ periodic orbits of $X_{A}$ , there are finitely many $(m,n)\in \mathbb {Z}^{2}$ such that $Z_{m,n}$ is a suspension flow.

10 Explicit examples

In this section we consider more specifically the orbits of $(0,0)$ and $(\tfrac 12,\tfrac 12)$ . For any $A\in SL(2,{\mathbb Z})$ the point $(0,0)$ is a fixed point of $f_{A}$ , but for the point $(\tfrac 12,\tfrac 12)$ there are three possibilities:

• • either $(\tfrac 12,\tfrac 12)$ is a fixed point,

• • or $(\tfrac 12,\tfrac 12)$ is a periodic point of period $2$ ,

• • or it is a periodic point of period $3$ , whose orbit is exactly

  $$ \begin{align*}\{(0,\tfrac12),(\tfrac12,0),(\tfrac12,\tfrac12)\}.\end{align*} $$

For instance $(\tfrac 12,\tfrac 12)$ is a periodic of period $3$ (respectively, $2$ ) for every matrix of the form

$$ \begin{align*}A_{k}=\left(\begin{array}{@{}cc@{}} k&k-1\\ 1&1 \end{array}\right),\end{align*} $$

with $k\in 2{\mathbb N}^{*}$ (respectively, $k\in 2{\mathbb N}+3$ ).

Remark 10.1. Given any matrix $A\in SL(2,{\mathbb Z})$ , any positive or negative $(0,0)$ -rectangle contains a point of $\{(0,\tfrac 12),(\tfrac 12,0),(\tfrac 12,\tfrac 12)\}+{\mathbb Z}^{2}$

Indeed, a $(0,0)$ -primitive rectangle does not contain any other integer points and has a diagonal whose endpoint is an integer point. Therefore, the middle point of that diagonal cannot be an integer point, hence it belongs to $\{(0,\tfrac 12),(\tfrac 12,0),(\tfrac 12,\tfrac 12)\}+{\mathbb Z}^{2}$ . Using the previous remark and by applying Theorem 8, we have the following result.

Corollary 10.1. Given any matrix $A\in SL(2,{\mathbb Z})$ , consider any vector field Y obtained from $X_{A}$ by performing surgeries along the orbits corresponding to the set $\{(0,0), (0,\tfrac 12),(\tfrac 12,0),(\tfrac 12,\tfrac 12)\}$ such that the characteristic numbers associated to the points $\{(0,\tfrac 12),(\tfrac 12,0),(\tfrac 12,\tfrac 12)\}$ have the same sign $\omega \in \{+,-\}$ and are large enough. Then Y is ${\mathbb R}$ -covered and $\omega $ -twisted.

Also by our above remark, the triples $(X_{A_{k}},(0,0),\{(0,\tfrac 12),(\tfrac 12,0),(\tfrac 12,\tfrac 12)\})$ with $k\in 2{\mathbb N}^{*}$ provide infinitely many examples that realize case 2 of §9.

Consider now the matrix $B_{k}=A_{k}^{3}$ when $k\in 2{\mathbb N}^{*}$ and $B_{k}=A_{k}^{2}$ when $k\in 2{\mathbb N}+3$ .

Lemma 10.1. For any k, the Anosov map $f_{B_{k}}$ admits positive and negative $(0,0)$ - rectangles disjoint from $\widetilde {(\tfrac 12,\tfrac 12)}$ and positive and negative $(\tfrac 12,\tfrac 12)$ -rectangles disjoint from $\widetilde {(0,0)}$ .

Proof. Notice that the foliations of $A_{k}$ and $B_{k}$ coincide. We denote

$$ \begin{align*}F^{s}_{k}=F^{s}_{B_{k}}=F^{s}_{A_{k}}\quad\mbox{and}\quad F^{u}_{k}=F^{u}_{B_{k}}=F^{u}_{A_{k}}.\end{align*} $$

Because $A_{k}$ has positive coefficients its unstable direction is inside $(\mathbb {R}^{+})^{2}\cup (\mathbb {R}^{-})^{2}$ and its stable direction in $\mathbb {R}^{+}\times \mathbb {R}^{-} \cup \mathbb {R}^{-}\times \mathbb {R}^{+}$ , where $\mathbb {R}^{+}= [0, +\infty )$ and $\mathbb {R}^{-}= (-\infty ,0]$ .

By looking at the image of the $(\mathbb {R}^{+})^{2}$ quadrants one obtains that the unstable direction $E^{u}$ is between the increasing (usual) diagonal of ${\mathbb R}^{2}$ and the x-axis. In the same way, by looking at the inverse image of the $\mathbb {R}^{+}\times \mathbb {R}^{-}$ quadrant, one checks that the stable direction $E^{s}$ is between the decreasing diagonal and the y-axis.

One deduces by the previous observations that the $(0,0)$ -rectangle admitting $[0,1]\times \{0\}$ as a diagonal is a positive primitive $(0,0)$ -rectangle disjoint from $\widetilde {(\tfrac 12,\tfrac 12)}$ . In the same way, the $(0,0)$ -rectangle admitting $\{0\}\times [0,1]$ as a diagonal is a negative primitive $(0,0)$ -rectangle disjoint from $\widetilde {(\tfrac 12,\tfrac 12)}$ .

Finally, the translated by $(\tfrac 12,\tfrac 12)$ positive and negative $(0,0)$ -rectangles disjoint from $\widetilde {(\tfrac 12,\tfrac 12)}$ are respectfully positive and negative $(\tfrac 12,\tfrac 12)$ -rectangles disjoint from $\widetilde {(0,0)}$ , which concludes the proof.

The triples $(X_{B_{k}},(0,0),(\tfrac 12,\tfrac 12))$ provide infinitely many examples that realize the situation (1) of §9.