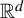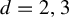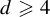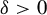The Assouad dimension of self-affine measures on sponges

Abstract

We derive upper and lower bounds for the Assouad and lower dimensions of self-affine measures in $\mathbb {R}^d$ generated by diagonal matrices and satisfying suitable separation conditions. The upper and lower bounds always coincide for $d=2,3$, yielding precise explicit formulae for those dimensions. Moreover, there are easy-to-check conditions guaranteeing that the bounds coincide for $d \geqslant 4$. An interesting consequence of our results is that there can be a ‘dimension gap’ for such self-affine constructions, even in the plane. That is, we show that for some self-affine carpets of ‘Barański type’ the Assouad dimension of all associated self-affine measures strictly exceeds the Assouad dimension of the carpet by some fixed $\delta>0$ depending only on the carpet. We also provide examples of self-affine carpets of ‘Barański type’ where there is no dimension gap and in fact the Assouad dimension of the carpet is equal to the Assouad dimension of a carefully chosen self-affine measure.

1 Introduction: dimensions of self-affine measures

Let $\nu $ be a compactly supported Borel probability measure in $\mathbb {R}^d$ . The Assouad and lower dimensions of $\nu $ quantify the extremal local fluctuations of the measure by considering the relative measure of concentric balls. In particular, a measure is doubling if and only if it has finite Assouad dimension; see, for example, [11, Lemma 4.1.1]. Write $\mathrm {supp}(\nu )$ to denote the support of $\nu $ and $|F|$ to denote the diameter of a non-empty set F. The Assouad dimension of $\nu $ is defined by

$$ \begin{align*} \dim_{\mathrm{A}} \nu=\inf \bigg\{s \geqslant 0: &\text{ there exists } C>0 \text{ such that, for all } x \in \mathrm{supp}(\nu) \\ &\text{ and for all } 0<r<R<|\mathrm{supp}(\nu)|, \frac{\nu(B(x, R))}{\nu(B(x, r))} \leqslant C\bigg(\frac{R}{r}\bigg)^{s}\bigg\}, \end{align*} $$

and, provided $|\mathrm {supp}(\nu )|>0$ , the lower dimension of $\nu $ is

$$ \begin{align*} \dim_{\mathrm{L}} \nu=\sup \bigg\{s \geqslant 0: &\text{ there exists } C>0 \text{ such that, for all } x \in \mathrm{supp}(\nu) \\ &\text{ and for all } 0<r<R<|\mathrm{supp}(\nu)|, \frac{\nu(B(x, R))}{\nu(B(x, r))} \geqslant C\bigg(\frac{R}{r}\bigg)^{s}\bigg\}. \end{align*} $$

If $|\mathrm {supp}(\nu )|=0$ , then $\dim _{\mathrm {L}} \nu =0$ . The Assouad and lower dimensions of measures were introduced by Käenmäki, Lehrbäck and Vuorinen [15], where they were originally referred to as the upper and lower regularity dimensions, respectively. We are interested in the Assouad and lower dimensions of self-affine measures.

Given a finite index set $\mathcal {I}=\{1,\ldots ,N\}$ , an affine iterated function system (IFS) on $\mathbb {R}^d$ is a finite family $\mathcal {F}=\{f_i\}_{i\in \mathcal {I}}$ of affine contracting maps $f_i(x)=A_i x+t_i$ . The IFS determines a unique, non-empty compact set F, called the attractor, which satisfies the relation

$$ \begin{align*} F = \bigcup_{i\in\mathcal{I}} f_i(F). \end{align*} $$

Given a probability vector $\mathbf {p}=(p(i))_{i\in \mathcal {I}}$ with strictly positive entries, the self-affine measure $\nu _{\mathbf {p}}$ fully supported on F is the unique Borel probability measure

$$ \begin{align*} \nu_{\mathbf{p}} = \sum_{i\in\mathcal{I}} p(i)\, \nu_{\mathbf{p}}\circ f_i^{-1}. \end{align*} $$

The measure $\nu _{\mathbf {p}} $ has an equivalent characterization as the pushforward of the Bernoulli measure generated by $\mathbf {p}$ under the natural projection from the symbolic space to the attractor. More precisely, given $\mathbf {p}$ , the Bernoulli measure on the symbolic space $\Sigma =\mathcal {I}^{\mathbb {N}}$ is the product measure $\mu _{\mathbf {p}}=\mathbf {p}^{\mathbb {N}}$ . The natural projection $\pi :\Sigma \to F$ is given by

(1.1) $$ \begin{align} \pi(\mathbf{i}) =\pi(i_1i_2\ldots i_k \ldots) := \lim_{k\to\infty} f_{i_1i_2\ldots i_k}(0), \end{align} $$

where $f_{i_1i_2\ldots i_k}=f_{i_1}\circ f_{i_2} \circ \cdots \circ f_{i_k}$ . Then $\nu _{\mathbf {p}} = \mu _{\mathbf {p}}\circ \pi ^{-1}$ .

Computing (or estimating) the dimensions of self-affine measures is a hard problem in general. Moreover, many self-affine measures fail to be doubling (and so have infinite Assouad dimension) and so some conditions are needed in order to obtain sensible results. The specific self-affine measures we are able to handle are those supported on ‘Barański type sponges’. That is, the $A_i$ are diagonal matrices and we assume a separation condition (the very strong separation of principal projections condition; see Definition 2.1) which, roughly speaking, says that all relevant projections of the measure satisfy the more familiar strong separation condition. For such measures we derive upper and lower bounds for the Assouad and lower dimensions; see Theorem 2.5. Moreover, the upper and lower bounds agree when $d=2,3$ (see Lemma 3.2) and also in many other cases in higher dimensions. It remains an interesting open problem whether our bounds are sharp in full generality; see Question 2.6. One of the main technical challenges in considering ‘Barański type sponges’ instead of, for example, those of Bedford–McMullen or Lalley–Gatzouras type is that we have to control the ratio of the measure of approximate cubes with ‘different orderings’. As such we develop a number of technical tools which may have further application, for example the subdivision argument used in proving Proposition 5.4. An interesting consequence of our results is that there can be a ‘dimension gap’ for such self-affine constructions, even in the plane; see Corollary 2.7 and Proposition 4.1.

2 Main results: dimension bounds and dimension gaps

2.1 Our model and assumptions

We call a self-affine set F a (self-affine) sponge if the linear part $A_i$ of each $f_i$ is a diagonal matrix with entries $(\unicode{x3bb} _i^{(1)},\ldots ,\unicode{x3bb} _i^{(d)})$ . When $d=2$ sponges are more commonly referred to as self-affine carpets, and when $d=1$ they are self-similar sets. The original model for the self-affine carpet was introduced independently by Bedford [3] and McMullen [20] and later generalized by Lalley and Gatzouras [18], Barański [1] and many others. The dimension theory of self-affine carpets is well developed, although several interesting questions remain such as whether self-affine carpets necessarily support an invariant measure of maximal Hausdorff dimension; see [22]. A recent breakthrough established that this was false for sponges with $d=3$ [6], that is, the existence of a ‘dimension gap’ was established for certain examples. This dimension gap result resolved a long-standing open problem in dynamical systems.

Generally, much less is known about sponges in dimensions $d\geqslant 3$ . The objective of this paper is to contribute to this line of research. A number of results concern the higher-dimensional Bedford–McMullen sponges; see Example 2.4 for the formal definition. Their Hausdorff and box dimensions were determined by Kenyon and Peres [16], while their Assouad and lower dimensions were calculated by Fraser and Howroyd [12]. Olsen [21] studied multifractal properties of self-affine measures supported by these sponges, and Fraser and Howroyd [13] derived a formula for the Assouad dimension of such measures. The lower and Assouad dimensions of Lalley–Gatzouras sponges (see Example 2.3) are also known [5, 14].

Without loss of generality we assume that $f_i([0,1]^d)\subset [0,1]^d$ and that there is no $i\neq j$ such that $f_i(x)=f_j(x)$ for every $x\in [0,1]^d$ . To avoid unwanted complications with notation, we also assume that

$$ \begin{align*} \unicode{x3bb}_i^{(n)}\in(0,1)\quad \text{for every } i\in\mathcal{I} \text{ and } 1\leqslant n\leqslant d. \end{align*} $$

We make one further simplification by assuming that all pairs of coordinates are distinguishable, that is,

(2.1) $$ \begin{align} \text{for any } m\neq n\in\{1,\ldots,d\}\quad \text{there exists } i\in\mathcal{I} \text{ such that } \unicode{x3bb}_i^{(n)} \neq \unicode{x3bb}_i^{(m)}. \end{align} $$

Otherwise, the sponge is not ‘genuinely self-affine’ in all coordinates. The case when not all pairs of coordinates are distinguishable can be handled by ‘gluing’ together non-distinguishable coordinates, as was done by Howroyd [14], but we omit further discussion of such examples.

The orthogonal projections of F onto the principal n-dimensional subspaces play a vital role in our arguments. Let $\mathcal {S}_d$ be the symmetric group on the set $\{1,\ldots ,d\}$ . For a permutation $\sigma =(\sigma _1,\ldots ,\sigma _d)\in \mathcal {S}_d$ of the coordinates, let $E_n^{\sigma }$ denote the n-dimensional subspace spanned by the coordinate axes indexed by $\sigma _1,\ldots ,\sigma _n$ . Notice that $E_n^{\sigma }=E_n^{\omega }$ as long as $\{\sigma _1,\ldots ,\sigma _n\}$ and $\{\omega _1,\ldots ,\omega _n\}$ are the same sets. The permutation appears in the notation rather than just the set of indices because the ordering of coordinates will play a role in how the subspace is ‘built up’ from its lower-dimensional subspaces. Let $\Pi _n^{\sigma }:[0,1]^d\to E_n^\sigma $ be the orthogonal projection onto $E_n^{\sigma }$ . For $n=d$ , $\Pi _d^{\sigma }$ is simply the identity map. We say that $f_i$ and $f_j$ overlap exactly on $E_n^{\sigma }$ if

$$ \begin{align*} \Pi_n^{\sigma}(f_i(x))=\Pi_n^{\sigma}(f_j(x)) \quad\text{for every } x\in[0,1]^d. \end{align*} $$

Observe that if $f_i$ and $f_j$ overlap exactly on $E_n^{\sigma }$ then they also overlap exactly on $E_m^{\sigma }$ for all $1\leqslant m \leqslant n$ but may not overlap exactly on any $E_n^{\sigma '}$ for some other $\sigma '\in \mathcal {S}_d$ .

Recall that $\Sigma = \mathcal {I}^{\mathbb {N}}$ is the space of all one-sided infinite words $\mathbf {i}=i_1,i_2,\ldots .$ In a slight abuse of notation, we also write $\mathbf {i}=i_1,\ldots ,i_k\in \mathcal {I}^k$ for a finite-length word or $\mathbf {i}|k=i_1,\ldots ,i_k$ for the truncation of $\mathbf {i}\in \Sigma $ . For $r>0$ , the r-stopping of $\mathbf {i}\in \Sigma $ in the nth coordinate (for $n=1,\ldots ,d$ ) is the unique integer $L_{\mathbf {i}}(r,n)$ for which

(2.2) $$ \begin{align} \prod_{\ell=1}^{L_{\mathbf{i}}(r,n)} \unicode{x3bb}_{i_\ell}^{(n)} \leqslant r < \prod_{\ell=1}^{L_{\mathbf{i}}(r,n)-1}\unicode{x3bb}_{i_\ell}^{(n)}. \end{align} $$

We distinguish between two different kinds of orderings. We say that $\mathbf {i}\in \Sigma $ determines a $\sigma $ -ordered cylinder at scale r if $\sigma _d=\sigma _d(\mathbf {i},r)$ is the largest index that satisfies

$$ \begin{align*} L_{\mathbf{i}}(r,\sigma_d)=\min_{n\in\{1,\ldots,d\}} L_{\mathbf{i}}(r,n) \quad\text{and}\quad \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_d)} = \min_{n\in\{1,\ldots,d\}} \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(n)}, \end{align*} $$

and then

(2.3) $$ \begin{align} \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_d)} \leqslant \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_{d-1})} \leqslant \cdots \leqslant \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_1)}, \end{align} $$

where, to make the ordering unique, we use the convention that

$$ \begin{align*} \text{ if }\; \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_n)} = \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_{d})} \unicode{x3bb}_{i_{\ell}}^{(\sigma_{n-1})} \quad\text{then } \sigma_n>\sigma_{n-1}. \end{align*} $$

It is a strictly $\sigma $ -ordered cylinder if all inequalities in (2.3) are strict. This corresponds to the ordering of the length of the sides of the cylinder set $f_{\mathbf {i}|L_{\mathbf {i}}(r,\sigma _d)}([0,1]^d)$ with $\sigma _d$ corresponding to the shortest side and $\sigma _1$ the longest. Moreover, we say that $\mathbf {i}\in \Sigma $ determines a $\sigma $ -ordered cube at scale r if

(2.4) $$ \begin{align} L_{\mathbf{i}}(r,\sigma_d)\leqslant L_{\mathbf{i}}(r,\sigma_{d-1})\leqslant \cdots\leqslant L_{\mathbf{i}}(r,\sigma_1). \end{align} $$

Here the ordering is made unique with the following rule: if coordinates $k<m$ satisfy $L_{\mathbf {i}}(r,k)=L_{\mathbf {i}}(r,m)$ , then k precedes m in $\sigma $ if and only if $\prod _{\ell =1}^{L_{\mathbf {i}}(r,k)} \unicode{x3bb} _{i_{\ell }}^{(k)} \geqslant \prod _{\ell =1}^{L_{\mathbf {i}}(r,k)} \unicode{x3bb} _{i_{\ell }}^{(m)}$ . This corresponds to the ordering of the sides of a symbolic approximate cube to be formally introduced in §5. Note that the ordering of $\mathbf {i}$ as a cylinder or as a cube at a scale r need not be the same. Of importance are the different orderings that are ‘witnessed’ by an $\mathbf {i}\in \Sigma $ at some scale r:

(2.5) $$ \begin{align} \mathcal{A}:= \{ \sigma\in\mathcal{S}_d:\ &\text{there exist } \mathbf{i}\in\Sigma \text{ and } r>0 \text{ such that } \nonumber\\ & \mathbf{i} \text{ determines a } \sigma\text{-ordered cube at scale } r \} \end{align} $$

and

(2.6) $$ \begin{align} \mathcal{B}:= \{ \sigma\in\mathcal{S}_d:\ &\text{there exist } \mathbf{i}\in\Sigma \text{ and } r>0 \text{ such that } \nonumber\\ & \mathbf{i} \text{ determines a strictly } \sigma\text{-ordered cylinder at scale } r \}. \end{align} $$

Clearly $\mathcal {B}\subseteq \mathcal {A}$ because if $\sigma \in \mathcal {B}$ is witnessed by $\mathbf {j}$ at scale r, then by defining $\mathbf {i}:= \overline {\mathbf {j}|L_{\mathbf {j}}(r,\sigma _d)}$ , that is, repeating the word $\mathbf {j}|L_{\mathbf {j}}(r,\sigma _d)$ infinitely often, there is $r'$ small enough such that (2.4) holds. We give a more detailed account of the relationship between $\mathcal {A}$ and $\mathcal {B}$ in §3, where we show that $\mathcal {A} = \mathcal {B}$ for $d=2$ and $3$ , but also present a four-dimensional example for which $\mathcal {B}\subset \mathcal {A}$ . A simple example to determine $\mathcal {A}$ and $\mathcal {B}$ is when the sponge F satisfies the coordinate ordering condition, that is, there exists a permutation $\sigma \in \mathcal {S}_d$ such that

(2.7) $$ \begin{align} 0<\unicode{x3bb}_i^{(\sigma_d)}\leqslant\unicode{x3bb}_i^{(\sigma_{d-1})}\leqslant\cdots\leqslant\unicode{x3bb}_i^{(\sigma_1)}<1 \quad\text{for every } i\in\mathcal{I}. \end{align} $$

In this case, $L_{r}(\mathbf {i},\sigma _d)\leqslant L_{r}(\mathbf {i},\sigma _{d-1})\leqslant \cdots \leqslant L_{r}(\mathbf {i},\sigma _1)$ for every $\mathbf {i}\in \Sigma $ and $r>0$ , hence $\mathcal {A}=\mathcal {B}=\{\sigma \}$ and only the projections $\Pi _n^{\sigma }F$ play a role in the study of F.

For each permutation $\sigma \in \mathcal {A}$ we define index sets $\mathcal {I}_d^{\sigma }\supseteq \mathcal {I}_{d-1}^{\sigma }\supseteq \cdots \supseteq \mathcal {I}_1^{\sigma }$ with $\mathcal {I}_d^{\sigma }:= \mathcal {I}$ as follows. Initially set $\mathcal {I}_d^{\sigma }= \mathcal {I}_{d-1}^{\sigma }= \cdots = \mathcal {I}_1^{\sigma }$ and then repeat the following procedure for all pairs $i<j$ ( $i,j\in \mathcal {I}$ ). Starting from $n=d-1$ and decreasing n, check whether $f_i$ and $f_j$ overlap exactly on $E_n^{\sigma }$ . If they do not overlap exactly for any n, then move onto the next pair $(i,j)$ , otherwise, take the largest $n'$ for which $f_i$ and $f_j$ overlap exactly and remove j from $\mathcal {I}_{n'}^{\sigma },\mathcal {I}_{n'-1}^{\sigma },\ldots , \mathcal {I}_{1}^{\sigma }$ and then move onto the next pair $(i,j)$ . The sets $\mathcal {I}_{d-1}^{\sigma }, \ldots , \mathcal {I}_1^{\sigma }$ are what remain after repeating this procedure for all pairs $i<j$ . In a further abuse of notation, we denote by $\Pi _n^{\sigma }: \mathcal {I}\to \mathcal {I}_n^{\sigma }$ the ‘projection’ of $j\in \mathcal {I}$ onto $\mathcal {I}_n^{\sigma }$ , that is,

$$ \begin{align*} \Pi_n^{\sigma}j=i \quad\text{if } f_i \text{ and } f_j \text{ overlap exactly on } E_n^{\sigma} \text{ and } i\in\mathcal{I}_n^{\sigma}. \end{align*} $$

Defining $\Sigma _{n}^{\sigma }:= (\mathcal {I}_{n}^{\sigma })^{\mathbb {N}}$ , we also let $\Pi _n^{\sigma }: \Sigma \to \Sigma _{n}^{\sigma }$ by acting coordinatewise, that is, $\Pi _n^{\sigma }\mathbf {i}=\Pi _n^{\sigma } i_1,\Pi _n^{\sigma }i_2,\ldots .$ For completeness, let $\Pi _d^{\sigma }$ be the identity map on $\Sigma $ .

Definition 2.1. A self-affine sponge $F\subset [0,1]^d$ satisfies the separation of principal projections condition (SPPC) if for every $\sigma \in \mathcal {A}$ , $1\leqslant n\leqslant d$ and $i,j\in \mathcal {I}$ ,

(2.8) $$ \begin{align} \kern-10pt\text{either } f_i \text{ and } f_j \text{ overlap exactly on } E_n^{\sigma} \text{ or } \Pi_n^{\sigma}(f_i((0,1)^d))\cap \Pi_n^{\sigma}(f_j((0,1)^d)) = \emptyset. \end{align} $$

The sponge satisfies the very strong SPPC if $(0,1)^d$ can be replaced with $[0,1]^d$ .

If (2.8) is only assumed for $n=d$ , the rather weaker condition is known as the rectangular open set condition; see, for example, [9]. The following are the natural generalizations of Barański [1], Lalley–Gatzouras [18] and Bedford–McMullen [3, 20] carpets to higher dimensions.

Example 2.2. A Barański sponge $F\subset [0,1]^d$ satisfies that for all $\sigma \in \mathcal {S}_d$ and $i,j\in \mathcal {I}$ ,

$$ \begin{align*} \text{either } f_i \text{ and } f_j \text { overlap exactly on } E_1^{\sigma} \text{ or } \Pi_1^{\sigma}(f_i((0,1)^d))\cap \Pi_1^{\sigma}(f_j((0,1)^d)) = \emptyset. \end{align*} $$

In other words, the IFSs generated on the coordinate axes by indices $\mathcal {I}_1^{\sigma }$ satisfy the open set condition. This clearly implies the SPPC.

Example 2.3. A Lalley–Gatzouras sponge $F\subset [0,1]^d$ satisfies the SPPC and the coordinate ordering condition (2.7) for some $\sigma \in \mathcal {S}_d$ .

Example 2.4. A Bedford–McMullen sponge $F\subset [0,1]^d$ is a Barański sponge which satisfies the coordinate ordering condition (hence, is also a Lalley–Gatzouras sponge) and

$$ \begin{align*} \unicode{x3bb}_1^{(n)} = \unicode{x3bb}_2^{(n)} =\cdots = \unicode{x3bb}_N^{(n)} \quad\text{for all } 1\leqslant n\leqslant d. \end{align*} $$

Observe that a carpet on the plane satisfies the SPPC if and only if it is either Barański (when $\#\mathcal {A}=2$ ) or Lalley–Gatzouras (when $\#\mathcal {A}=1$ ). Therefore, this definition combines these two classes in a natural way. Moreover, for dimensions $d\geqslant 3$ it is a wider class of sponges than simply the union of the Barański and Lalley–Gatzouras class. For $d=3$ , we give a complete characterization of the new classes that emerge in §4.2.

The very strong SPPC is a natural extension of the very strong separation condition first introduced by King [17] to study the fine multifractal spectrum of self-affine measures on Bedford–McMullen carpets. It was later adapted to higher-dimensional Bedford–McMullen sponges by Olsen [21]. It is also assumed by Fraser and Howroyd [12, 13] when calculating the Assouad dimension of self-affine measures on these sponges. In fact, in this case the very strong separation condition is a necessary assumption. Without it one can construct a carpet which does not carry any doubling self-affine measure; see [12, §4.2] for an example.

2.2 Main result

In order to state our main result we need to introduce additional probability vectors derived from $\mathbf {p}=(p(i))_{i\in \mathcal {I}}$ by ‘projecting’ it onto subsets $\mathcal {I}_n^{\sigma }\subseteq \mathcal {I}$ . For $\sigma \in \mathcal {A}$ and $1\leqslant n\leqslant d-1$ let

$$ \begin{align*} \mathbf{p}_n^{\sigma}:= ( p_n^{\sigma}(i) )_{i\in\mathcal{I}_n^{\sigma}}\quad\text{where } p_n^{\sigma}(i):= \sum_{j\in\mathcal{I}: \Pi_n^{\sigma}j=i} p(j). \end{align*} $$

Observe that due to the SPPC, $p_n^{\sigma }(i)$ can also be calculated by

(2.9) $$ \begin{align} p_n^{\sigma}(i)= \sum_{j\in\mathcal{I}_{n+1}^{\sigma,i}} p_{n+1}^{\sigma}(j) \quad\text{where } \mathcal{I}_{n+1}^{\sigma,i}:= \{ j\in\mathcal{I}_{n+1}^{\sigma}: \Pi_n^{\sigma}j=i \}. \end{align} $$

This gives rise to the conditional measure $\mathbf {P}_{n-1}^{\sigma ,i}=( P_{n-1}^{\sigma ,i}(j))_{j\in \mathcal {I}_{n}^{\sigma ,i}}$ along the fibre $i\in \mathcal {I}_{n-1}^{\sigma }$ for $1\leqslant n\leqslant d$ by setting

$$ \begin{align*} P_{n-1}^{\sigma,i}(j) := \frac{p_n^{\sigma}(j)}{p_{n-1}^{\sigma}(i)}, \end{align*} $$

where if $n=1$ we define $\Pi _0^{\sigma }i=\emptyset , \mathcal {I}_0^{\sigma }=\{\emptyset \}$ and $p_0^{\sigma }(\emptyset )=1$ . This is a natural extension of the conditional probabilities introduced by Olsen [21] for Bedford–McMullen sponges. For $m\geqslant n$ and $i\in \mathcal {I}_{m}^{\sigma }$ , we slightly simplify notation by writing

(2.10) $$ \begin{align} P_{n-1}^{\sigma}(\Pi_{n}^{\sigma}i) = P_{n-1}^{\sigma,\Pi_{n-1}^{\sigma}i}(\Pi_{n}^{\sigma}i). \end{align} $$

A specific choice of $\mathbf {p}$ has particular importance. For $i\in \mathcal {I}_n^{\sigma }$ ( $0\leqslant n\leqslant d-1$ ), define $s_n^{\sigma }(i)$ to be the unique number which satisfies the equation

$$ \begin{align*} \sum_{j\in\mathcal{I}_{n+1}^{\sigma,i}} ( \unicode{x3bb}_j^{(\sigma_{n+1})} )^{s_n^{\sigma}(i)}=1. \end{align*} $$

This is the similarity dimension of the IFS given by the ‘fibre above’ i. The SPPC implies that $s_n^{\sigma }(i)\in [0,1]$ . We define the $\sigma $ -ordered coordinatewise natural measure as

(2.11) $$ \begin{align} \mathbf{q}^{\sigma} = (q^{\sigma}(i))_{i\in\mathcal{I}} \quad\text{where } q^{\sigma}(i):= \prod_{n=1}^d ( \unicode{x3bb}_{\Pi_n^{\sigma} i}^{(\sigma_n)} )^{s_{n-1}^{\sigma}(\Pi_{n-1}^{\sigma} i)}. \end{align} $$

For Bedford–McMullen sponges, Fraser and Howroyd [12] used the terminology ‘coordinate uniform measure’ since in that case the natural measure along a fibre simplifies to the uniform measure. This measure has the special property that

$$ \begin{align*} q_n^{\sigma}(i) = \sum_{j\in\mathcal{I}: \Pi_n^{\sigma}j=i} q^{\sigma}(j) = \prod_{m=1}^n ( \unicode{x3bb}_{\Pi_m^{\sigma} i}^{(\sigma_m)} )^{s_{m-1}^{\sigma}(\Pi_{m-1}^{\sigma} i)}. \end{align*} $$

We are now ready to state our main result.

Theorem 2.5. Let $\nu _{\mathbf {p}}$ be a self-affine measure fully supported on a self-affine sponge satisfying the very strong SPPC. Then

$$ \begin{align*} \max_{\sigma\in\mathcal{B}}\, \overline{S}(\mathbf{p},\sigma) \leqslant \dim_{\mathrm{A}} \nu_{\mathbf{p}} \leqslant \max_{\sigma\in\mathcal{A}}\, \overline{S}(\mathbf{p},\sigma) \end{align*} $$

and

$$ \begin{align*} \min_{\sigma\in\mathcal{A}}\, \underline{S}(\mathbf{p},\sigma) \leqslant \dim_{\mathrm{L}} \nu_{\mathbf{p}} \leqslant \min_{\sigma\in\mathcal{B}}\, \underline{S}(\mathbf{p},\sigma) , \end{align*} $$

where

$$ \begin{align*} \overline{S}(\mathbf{p},\sigma) := \sum_{n=1}^{d}\, \max_{i\in\mathcal{I}_n^{\sigma}} \frac{ \log P_{n-1}^{\sigma}(i) }{ \log \unicode{x3bb}_{i}^{(\sigma_n)} } \quad\text{and}\quad \underline{S}(\mathbf{p},\sigma) := \sum_{n=1}^{d}\, \min_{i\in\mathcal{I}_n^{\sigma}} \frac{ \log P_{n-1}^{\sigma}(i) }{ \log \unicode{x3bb}_{i}^{(\sigma_n)} }. \end{align*} $$

In particular, for the $\sigma $ -ordered coordinatewise natural measure,

$$ \begin{align*} \overline{S}(\mathbf{q}^{\sigma} ,\sigma) = s_0^{\sigma}(\emptyset) + \sum_{n=1}^{d-1}\, \max_{i\in\mathcal{I}_n^{\sigma}} s_n^{\sigma}(i) \quad\text{and}\quad \underline{S}(\mathbf{q}^{\sigma} ,\sigma) = s_0^{\sigma}(\emptyset) + \sum_{n=1}^{d-1}\, \min_{i\in\mathcal{I}_n^{\sigma}} s_n^{\sigma}(i). \end{align*} $$

Symbolic arguments used in our proof are collected in §5, while the theorem itself is proved in §6. The result generalizes the formula in [13, Theorem 2.6] for $\dim _{\mathrm {A}} \nu _{\mathbf {p}}$ in the case of Bedford–McMullen sponges. A sufficient condition for the lower and upper bounds to coincide is if $\mathcal {A}=\mathcal {B}$ . This occurs when F is a Lalley–Gatzouras sponge in any dimension; moreover, we prove in §3 that $\mathcal {A}=\mathcal {B}$ for all F satisfying the SPPC in dimensions $d=2$ and $3$ . However, $\mathcal {A}=\mathcal {B}$ is not a necessary condition. We give an example in four dimensions for which the lower and upper bounds coincide even though $\mathcal {B}\subset \mathcal {A}$ ; see Proposition 3.4. Finding a potential example for $\max _{\sigma \in \mathcal {B}}\, \overline {S}(\mathbf {p},\sigma ) < \max _{\sigma \in \mathcal {A}} \overline {S}(\mathbf {p},\sigma )$ seems to be a more delicate matter and is a natural direction for further research.

Question 2.6. Is it true that $\max _{\sigma \in \mathcal {B}} \overline {S}(\mathbf {p},\sigma ) = \max _{\sigma \in \mathcal {A}} \overline {S}(\mathbf {p},\sigma )$ even if $\mathcal {B}\subset \mathcal {A}$ ? If not, then what is the correct value of $\dim _{\mathrm {A}}\nu _{\mathbf {p}}$ ?

2.3 A dimension gap: examples and non-examples

Very often it is the case that one of the bounds to determine some dimension of a set is obtained by calculating the respective dimension of measures supported by the set. For example, for the Assouad dimension Luukkainen and Saksman [19] and for the lower dimension Bylund and Gudayol [4] proved that if $F \subseteq \mathbb {R}^d$ is closed, then

$$ \begin{align*} \dim_{\mathrm{A}} F=\inf \{\dim_{\mathrm{A}} \nu: \mathrm{supp}(\nu)=F\} \end{align*} $$

and

$$ \begin{align*} \dim_{\mathrm{L}} F=\sup \{\dim_{\mathrm{L}} \nu: \mathrm{supp}(\nu)=F\}. \end{align*} $$

The well-known mass distribution principle and Frostman’s lemma combine to provide a similar result for the Hausdorff dimension; see, for example, [7]. There is also a relatively new notion of box or ‘Minkowski’ dimension for measures and again there is a similar result; see [8, Theorem 2.1]. Therefore, it is interesting to see whether the dimension of a set is still attained by restricting to a certain class of measures (e.g., dynamically invariant measures) or if there is a strictly positive ‘dimension gap’.

Self-affine measures supported on carpets and sponges have been used to showcase both kinds of behaviour. Here we just give a few highlights and direct the interested reader to the book [11, Ch. 8.5] for a more in-depth discussion. The Hausdorff dimension of a Lalley–Gatzouras carpet is attained by a self-affine measure [18]; however, this is not the case in higher dimensions by the counterexample of Das and Simmons [6]. The box dimension of a Bedford–McMullen carpet is attained by a self-affine measure if and only if the carpet has uniform fibres; see [2]. The Assouad and lower dimensions of a Lalley–Gatzouras sponge are simultaneously realized by the same self-affine measure, namely the coordinatewise natural measure [14].

Going beyond the Lalley–Gatzouras class, one might expect that if $\mathcal {A}=\mathcal {B}$ then one of the coordinatewise natural measures could still realize the Assouad dimension and potentially another the lower dimension. An interesting corollary of Theorem 2.5 is that this is not the case in general. A strictly positive dimension gap can occur on the plane, noting that $\dim _{\mathrm {A}}F$ and $\dim _{\mathrm {L}}F$ were calculated by Fraser [10] using covering arguments.

Corollary 2.7. There exists a Barański carpet F such that

(2.12) $$ \begin{align} \inf_{\mathbf{p}} \dim_{\mathrm{A}} \nu_{\mathbf{p}} \geqslant \dim_{\mathrm{A}} F+\delta_F \end{align} $$

for some $\delta _F>0$ depending only on F. Moreover, there also exists a Barański carpet E such that $\dim _{\mathrm {A}} E= \dim _{\mathrm {A}} \nu _{\mathbf {q}^{(1,2)}}$ .

These families of examples are presented in §4.1. Finding conditions under which there is a dimension gap also seems a delicate issue.

Question 2.8. Is it possible to give simple necessary and/or sufficient conditions for general self-affine carpets satisfying the very strong SPPC for there to be a dimension gap in the sense of (2.12)?

An unfortunate consequence of Corollary 2.7 is that in general the class of self-affine measures is insufficient to use in order to determine $\dim _{\mathrm {A}}F$ .

Question 2.9. What class $\mathcal {P}$ of measures should be used on the plane to ensure $\inf _{\nu \in \mathcal {P}} \dim _{\mathrm {A}} \nu = \dim _{\mathrm {A}} F$ ? For example, can $\mathcal {P}$ be taken to be the set of invariant measures?

3 Comparing orderings of cubes and cylinders

In this section we establish some further relationships between $\mathcal {A}$ and $\mathcal {B}$ ; recall (2.5) and (2.6). We say that coordinate x dominates coordinate y, denoted $y\prec x$ , if

(3.1) $$ \begin{align} \unicode{x3bb}_i^{(y)} \leqslant \unicode{x3bb}_i^{(x)} \quad\text{for every } i\in\mathcal{I}. \end{align} $$

Since any two coordinates $x\neq y$ are distinguishable (2.1), there actually exists an i for which the inequality is strict. A consequence of (3.1) is that $L_{\mathbf {i}}(r,y)\leqslant L_{\mathbf {i}}(r,x)$ for all $\mathbf {i}\in \Sigma $ and $r>0$ ; therefore, x must precede y in any $\sigma \in \mathcal {A}$ . As a result, if there is a chain of coordinates $x_n\prec x_{n-1}\prec \cdots \prec x_1$ , then $\#\mathcal {A}\leqslant d!/n!$ . Moreover, if $y\prec x$ , then the orthogonal projection onto the $(x,y)$ -plane must be a Lalley–Gatzouras carpet with coordinate x the dominant, while if neither dominates the other, then the projection is a Barański carpet. In general, we say F is a genuine Barański sponge if there do not exist coordinates $x,y$ with $x \prec y$ . An example with two maps is if $\unicode{x3bb} _1^{(d)}<\unicode{x3bb} _1^{(d-1)}<\cdots <\unicode{x3bb} _1^{(1)}$ and $\unicode{x3bb} _2^{(1)}<\unicode{x3bb} _2^{(2)}<\cdots <\unicode{x3bb} _2^{(d)}$ .

We start with a useful equivalent characterization of $\mathcal {B}$ by a condition on the maps of the IFS. Let $\mathcal {P}_{\mathcal {I}}$ denote the set of all probability vectors on $\mathcal {I}$ . For a coordinate x and $\mathbf {p}\in \mathcal {P}_{\mathcal {I}}$ , we define the Lyapunov exponent to be $\chi _x(\mathbf {p}) := -\sum _{i\in \mathcal {I}}p(i)\log \unicode{x3bb} _i^{(x)}$ . Observe that if $y\prec x$ , then $\chi _{x}(\mathbf {p}) < \chi _{y}(\mathbf {p})$ for every $\mathbf {p}\in \mathcal {P}_{\mathcal {I}}$ . The following lemma shows that to determine $\mathcal {B}$ it is enough to see how $\mathcal {P}_{\mathcal {I}}$ gets partitioned by the different orderings of Lyapunov exponents.

Lemma 3.1. An ordering $\sigma \in \mathcal {B}$ if and only if there exists $\mathbf {p}\in \mathcal {P}_{\mathcal {I}}$ such that $\chi _{\sigma _1}(\mathbf {p}) < \chi _{\sigma _2}(\mathbf {p}) < \cdots < \chi _{\sigma _d}(\mathbf {p})$ .

Proof. By introducing the empirical probability vector $\mathbf {t}_{\mathbf {i}}^K=(t_{\mathbf {i}}^K(i))_{i\in \mathcal {I}}$ with coordinate

$$ \begin{align*} t_{\mathbf{i}}^K(i):= \frac{1}{K} \#\{1\leqslant k\leqslant K: i_{k}=i\} \end{align*} $$

for $\mathbf {i}\in \Sigma $ , $K\in \mathbb {N}$ and $i\in \mathcal {I}$ , we can express for any coordinate n,

$$ \begin{align*} \prod_{\ell=1}^{K} \unicode{x3bb}_{i_{\ell}}^{(n)} = \prod_{i\in\mathcal{I}} ( \unicode{x3bb}_{i}^{(n)} )^{K\cdot t_{\mathbf{i}}^K(i)} = \exp\bigg[ K\sum_{i\in\mathcal{I}}t_{\mathbf{i}}^K(i)\log \unicode{x3bb}_{i_{\ell}}^{(n)} \bigg] = \exp [ -K\cdot \chi_n(\mathbf{t}_{\mathbf{i}}^K) ]. \end{align*} $$

By definition, if $\sigma \in \mathcal {B}$ then there exist $\mathbf {i}\in \Sigma $ and $r>0$ such that

$$ \begin{align*} \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_d)} < \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_{d-1})} <\cdots < \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_d)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_1)}. \end{align*} $$

This clearly implies $\chi _{\sigma _1}(\mathbf {p}) < \chi _{\sigma _2}(\mathbf {p}) < \cdots < \chi _{\sigma _d}(\mathbf {p})$ with $\mathbf {p}=\mathbf {t}_{\mathbf {i}}^{L_{\mathbf {i}}(r,\sigma _d)}$ .

Conversely, if $\chi _{\sigma _1}(\mathbf {p}) < \chi _{\sigma _2}(\mathbf {p}) < \cdots < \chi _{\sigma _d}(\mathbf {p})$ then there also exists $\mathbf {q}\in \mathcal {P}_{\mathcal {I}}$ arbitrarily close to $\mathbf {p}$ with the property that each element has the form $q(i)=a_i/K$ for some $a_i,K\in \mathbb {N}$ and still $\chi _{\sigma _1}(\mathbf {q}) < \chi _{\sigma _2}(\mathbf {q}) < \cdots < \chi _{\sigma _d}(\mathbf {q})$ . Then any $\mathbf {i}\in \Sigma $ such that $\mathbf {t}_{\mathbf {i}}^K=\mathbf {q}$ and $r=\prod _{\ell =1}^{K} \unicode{x3bb} _{i_{\ell }}^{(\sigma _d)}$ shows that $\sigma \in \mathcal {B}$ .

Consider the set $\mathcal {Q}:= \{\mathbf {p}\in \mathcal {P}_{\mathcal {I}}: \text {there exist } x\neq y \text { such that } \chi _{x}(\mathbf {p}) = \chi _{y}(\mathbf {p})\}$ . This is the union of lower-dimensional slices of $\mathcal {P}_{\mathcal {I}}$ . Since all pairs of coordinates are distinguishable (2.1), for every $\mathbf {q}\in \mathcal {Q}$ with $\chi _{\sigma _1}(\mathbf {q}) \leqslant \chi _{\sigma _2}(\mathbf {q}) \leqslant \cdots \leqslant \chi _{\sigma _d}(\mathbf {q})$ there exists $\mathbf {p}\in \mathcal {P}_{\mathcal {I}}\setminus \mathcal {Q}$ with $\chi _{\sigma _1}(\mathbf {p}) < \chi _{\sigma _2}(\mathbf {p}) < \cdots < \chi _{\sigma _d}(\mathbf {p})$ . Therefore, dropping the word ‘strictly’ from the definition of $\mathcal {B}$ in (2.6) gives the same set of orderings.

The relationship $\mathcal {B}\subseteq \mathcal {A}$ always holds. It is interesting to see whether the inclusion is strict or not.

Lemma 3.2. If $d=2$ or $3$ , then $\mathcal {A}=\mathcal {B}$ for every sponge F satisfying the SPPC.

Proof. For $d=2$ the claim is automatic. For $d=3$ , choose $\sigma \in \mathcal {A}$ . Then there exist $\mathbf {i}\in \Sigma $ and $r>0$ such that $L_{\mathbf {i}}(r,\sigma _3)\leqslant L_{\mathbf {i}}(r,\sigma _{2})\leqslant L_{\mathbf {i}}(r,\sigma _1)$ . We claim that the cylinder $f_{\mathbf {i}|L_{\mathbf {i}}(r,\sigma _{2})}([0,1]^d)$ is $\sigma $ -ordered. Indeed, the way we have made the $\sigma $ -ordering unique implies that

$$ \begin{align*} \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_2)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_3)} \leqslant \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_2)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_2)} \leqslant \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_2)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_1)}, \end{align*} $$

which is equivalent to $\chi _{\sigma _1}(\mathbf {p}) \leqslant \chi _{\sigma _2}(\mathbf {p}) \leqslant \chi _{\sigma _3}(\mathbf {p})$ with $\mathbf {p}=\mathbf {t}_{\mathbf {i}}^{L_{\mathbf {i}}(r,\sigma _2)}$ . If the cylinder is not strictly $\sigma $ -ordered, then based on the discussion before Lemma 3.2 one can construct a strictly $\sigma $ -ordered cylinder from a small perturbation of $\mathbf {p}$ .

However, in four dimensions the inclusion $\mathcal {B}\subseteq \mathcal {A}$ can be strict. Our example relies on the following lemma.

Lemma 3.3. Assume the sponge F satisfying the SPPC is the attractor of an IFS consisting of two maps $f_1,f_2$ ordered $(2,1,3,4)$ and $(1,2,4,3)$ , respectively. Then

(3.2) $$ \begin{align} (1,2,3,4)\in\mathcal{B}\ {\Longleftrightarrow}\ (2,1,4,3)\notin\mathcal{B}\ {\Longleftrightarrow}\ \frac{\log ( \unicode{x3bb}_1^{(2)} / \unicode{x3bb}_1^{(1)} )}{\log ( \unicode{x3bb}_1^{(3)} / \unicode{x3bb}_1^{(4)} )} < \frac{\log ( \unicode{x3bb}_2^{(1)} / \unicode{x3bb}_2^{(2)} )}{\log ( \unicode{x3bb}_2^{(4)} / \unicode{x3bb}_2^{(3)} )}. \end{align} $$

Proof. Projection of F onto the $(1,2)$ -plane or the $(3,4)$ -plane is a Barański carpet while coordinates $3$ and $4$ are dominated by coordinates $1$ and $2$ . Therefore, $\mathcal {B}\subseteq \{(2,1,3,4),(1,2,4,3),(2,1,4,3),(1,2,3,4)\}$ .

Lemma 3.1 implies that $(1,2,3,4)\in \mathcal {B}$ if and only if there exists $\mathbf {p}=(p,1-p)$ such that $\chi _{1}(\mathbf {p}) < \chi _{2}(\mathbf {p}) < \chi _{3}(\mathbf {p}) < \chi _{4}(\mathbf {p})$ . Notice that $\chi _{2}(\mathbf {p}) < \chi _{3}(\mathbf {p})$ for any p because coordinate $2$ dominates coordinate $3$ . From the other two inequalities $\chi _{1}(\mathbf {p}) < \chi _{2}(\mathbf {p})$ and $\chi _{3}(\mathbf {p}) < \chi _{4}(\mathbf {p})$ , we can express p to obtain

(3.3) $$ \begin{align} \frac{\log ( \unicode{x3bb}_2^{(4)} / \unicode{x3bb}_2^{(3)} )}{\log ( (\unicode{x3bb}_2^{(4)}\unicode{x3bb}_1^{(3)}) / (\unicode{x3bb}_2^{(3)}\unicode{x3bb}_1^{(4)}) )} < p < \frac{\log ( \unicode{x3bb}_2^{(1)} / \unicode{x3bb}_2^{(2)} )}{\log ( (\unicode{x3bb}_2^{(1)}\unicode{x3bb}_1^{(2)}) / (\unicode{x3bb}_2^{(2)}\unicode{x3bb}_1^{(1)}) )}. \end{align} $$

Straightforward algebraic manipulations show that this is a non-empty interval if and only if the condition on the right-hand side of (3.2) holds.

Similarly, $(2,1,4,3)\in \mathcal {B}$ if and only if there exists $\mathbf {p}=(p,1-p)$ such that $\chi _{2}(\mathbf {p}) < \chi _{1}(\mathbf {p}) < \chi _{4}(\mathbf {p}) < \chi _{3}(\mathbf {p})$ . This gives the same condition for p as in (3.3) with the inequality signs reversed, which is equivalent to the reversed inequality in (3.2).

Proposition 3.4. There exists a sponge in four dimensions satisfying the very strong SPPC for which $\mathcal {B}\subset \mathcal {A}$ . Nonetheless, $\max _{\sigma \in \mathcal {B}} \overline {S}(\mathbf {p},\sigma ) = \max _{\sigma \in \mathcal {A}} \overline {S}(\mathbf {p},\sigma )$ .

Proof. The example consists of just two maps. Map $f_1$ is $(2,1,3,4)$ -ordered with

$$ \begin{align*} (\unicode{x3bb}_1^{(1)},\unicode{x3bb}_1^{(2)},\unicode{x3bb}_1^{(3)},\unicode{x3bb}_1^{(4)}) = (0.2, 0.4, 0.08, 0.02), \end{align*} $$

and $f_2$ is $(1,2,4,3)$ -ordered with

$$ \begin{align*} (\unicode{x3bb}_2^{(1)},\unicode{x3bb}_2^{(2)},\unicode{x3bb}_2^{(3)},\unicode{x3bb}_2^{(4)}) = (0.6, 0.3, 0.1, 0.2). \end{align*} $$

The translations can clearly be chosen so that the very strong SPPC holds. Moreover, $\mathcal {A}\subseteq \{(2,1,3,4),(1,2,4,3),(2,1,4,3),(1,2,3,4)\}$ for the same reason as in the proof of Lemma 3.3.

Our first claim is that $(1,2,3,4)\in \mathcal {A}$ . Some calculations show that choosing $r=5\times 10^{-5}$ and $\mathbf {i}=11112222222\ldots $ yields

$$ \begin{align*} L_{\mathbf{i}}(r,4) =3 < L_{\mathbf{i}}(r,3) =4 < L_{\mathbf{i}}(r,2) =10 < L_{\mathbf{i}}(r,1) =11. \end{align*} $$

It is also easy to check that the parameters do not satisfy the condition on the right-hand side of (3.2); hence, $(1,2,3,4)\notin \mathcal {B}$ by Lemma 3.3. A simple application of Theorem 2.5 shows that $\max _{\sigma \in \mathcal {B}}\, \overline {S}(\mathbf {p},\sigma ) = \max _{\sigma \in \mathcal {A}}\, \overline {S}(\mathbf {p},\sigma )$ .

4 Examples

4.1 Planar Barański carpets with different behaviour

The Assouad dimension of planar Barański carpets F was determined by Fraser [10]. Using our Theorem 2.5, we can check whether $\dim _{\mathrm {A}}F=\dim _{\mathrm {A}}\nu _{\mathbf {p}}$ for some self-affine measure $\nu _{\mathbf {p}}$ or if there is a dimension gap in the sense of (2.12). Surprisingly, both behaviours are witnessed by simple families of examples. Recall that in the Lalley–Gatzouras class $\dim _{\mathrm {A}}F$ is always achieved by the (only) coordinatewise natural measure.

Our first example shows a positive dimension gap. Let F be a Barański carpet which is not in the Lalley–Gatzouras class that satisfies the very strong SPPC with its first-level cylinders arranged in a way that there is no exact overlap when projecting to either coordinate axis; see the left-hand side of Figure 1 for an example. In particular, this contains all genuine Barański carpets defined by two maps. Let $a_i=\unicode{x3bb} _i^{(1)}$ and $b_i=\unicode{x3bb} _i^{(2)}$ , and define s and t to be the unique solutions to the equations

$$ \begin{align*} \sum_{i\in\mathcal{I}} a_i^s=1 \quad\text{and}\quad \sum_{i\in\mathcal{I}} b_i^t=1. \end{align*} $$

Without loss of generality we assume that $t\leqslant s$ . The very strong SPPC implies that $s<1$ . The formula from [10] shows that $\dim _{\mathrm {L}}F=t\leqslant s=\dim _{\mathrm {A}}F$ .

Figure 1 Defining maps for a Barański carpet with strictly positive dimension gap (left), and where the Assouad dimension of F is attained for correctly chosen parameters (right).

Proposition 4.1. For a Barański carpet F described above there is a strictly positive dimension gap, that is, there exists $\delta _F>0$ such that

$$ \begin{align*} \inf_{\mathbf{p}} \dim_{\mathrm{A}}\nu_{\mathbf{p}} \geqslant \dim_{\mathrm{A}}F + \delta_F. \end{align*} $$

Proof. The condition that there is no exact overlap when projecting to either coordinate axis implies that $p_1^{\sigma }(i)=p(i)$ and so $P_1^{\sigma }(i)=1$ for all $i\in \mathcal {I}=\{1,\ldots ,N\}$ . Applying Theorem 2.5, we immediately obtain

$$ \begin{align*} \dim_{\mathrm{A}}\nu_{\mathbf{p}} = \max\bigg\{ \frac{\log p(i)}{\log a_i}, \frac{\log p(i)}{\log b_i}: i\in\mathcal{I} \bigg\}. \end{align*} $$

Since F is not in the Lalley–Gatzouras class and $s\geqslant t$ , there exists $\ell \in \mathcal {I}$ such that $b_{\ell }^s>a_{\ell }^s$ . Fix $0<\varepsilon <b_{\ell }^s-a_{\ell }^s$ and first consider any $\mathbf {p}$ that satisfies $p(i)\leqslant a_i^s+\varepsilon $ for every $i\in \mathcal {I}$ . Then

$$ \begin{align*} \dim_{\mathrm{A}}\nu_{\mathbf{p}} \geqslant \frac{\log p(\ell)}{\log b_{\ell}} \geqslant \frac{\log (a_{\ell}^s+\varepsilon)}{\log b_{\ell}}> s \end{align*} $$

by the choice of $\varepsilon $ .

Now assume that $\mathbf {p}$ is such that there exists $j\in \mathcal {I}$ satisfying $p(j)>a_j^s+\varepsilon $ . Since $\sum _{i\in \mathcal {I}} a_i^s=1$ , the pigeonhole principle implies that there exists $k\in \mathcal {I}$ such that $0<p(k)\leqslant a_k^s-\varepsilon /(N-1)$ . Using this particular index,

$$ \begin{align*} \dim_{\mathrm{A}}\nu_{\mathbf{p}} \geqslant \frac{\log p(k)}{\log a_{k}} \geqslant \frac{\log( a_k^s -\varepsilon/(N-1))}{\log a_k} = s+ \frac{\log( (1- \varepsilon\cdot a_k^{-s}/(N-1) ))}{\log a_k}> s. \end{align*} $$

Therefore, choosing

$$ \begin{align*} \delta_F := \min \bigg\{ \frac{\log (a_{\ell}^s+\varepsilon)}{\log b_{\ell}} - s, \frac{\log( (1-\varepsilon\cdot a_k^{-s}/(N-1)))}{\log a_k} \bigg\} \end{align*} $$

completes the proof.

Proposition 4.1 shows that if a genuine Barański carpet whose Assouad dimension is realized by a self-affine measure exists, then its defining IFS must have at least three maps. Our second example shows that such a carpet does exist using only three maps. Giving a complete characterization for Barański carpets with three maps seems possible but perhaps tedious. However, it is straightforward to give an easy-to-check sufficient condition (valid for all Barański carpets) ensuring that the Assouad dimension of the carpet is attained by a Bernoulli measure. Comparing the formula from [10] with Theorem 2.5 shows that $\dim _{\mathrm {A}}F = \max _{\sigma \in \mathcal {A}}\overline {S}(\mathbf {q}^{\sigma } ,\sigma )$ . Therefore, if $\sigma $ satisfies $\overline {S}(\mathbf {q}^{\sigma } ,\sigma )\geqslant \max \{ \overline {S}(\mathbf {q}^{\omega } ,\omega ),\, \overline {S}(\mathbf {q}^{\sigma } ,\omega ) \}$ , then $\dim _{\mathrm {A}}F = \dim _{\mathrm {A}} \nu _{\mathbf {q}^{\sigma }}$ .

To demonstrate this, consider the Barański carpet whose first-level cylinders are depicted with the three shaded rectangles on the right-hand side of Figure 1. To ensure the attractor is a genuine Barański carpet, assume $a_1<b_1$ and $a_2> \min \{b_2,b_3\}$ . Define $r,s,t$ as follows: $b_2^r+b_3^r=1,\, a_1^s+a_2^s=1$ and $b_1^t+b_2^t+b_3^t=1$ . We assume $\max \{s,t\}<1$ so that the maps can be arranged in a way that satisfies the very strong SPPC. It follows from the formulas in [10] that $\dim _{\mathrm {A}}F = \max \{s+r,t\}$ .

Proposition 4.2. Consider a Barański carpet as on the right-hand side of Figure 1. Assume $s+r> t$ . If $a_2\geqslant \max \{b_2,b_3\}$ and $b_1^{1+r/s}\leqslant a_1<b_1$ , then $\dim _{\mathrm {A}} F= \dim _{\mathrm {A}} \nu _{\mathbf {q}^{\sigma }}$ for $\sigma =(1,2)$ .

Proof. Let $\sigma =(1,2)$ and $\omega =(2,1)$ . The vector $\mathbf {q}^{\sigma }$ is

$$ \begin{align*} q(1)=a_1^s,\quad q(2) = a_2^s\cdot b_2^r,\quad q(3) = a_2^s\cdot b_3^r. \end{align*} $$

A simple calculation gives $\overline {S}(\mathbf {q}^{\sigma } ,\sigma )=s+r=\dim _{\mathrm {A}} F$ , because we assume $s+r>t$ . Hence, it is enough to check when $\overline {S}(\mathbf {q}^{\sigma }, \omega )\leqslant s+r$ . Another calculation yields

$$ \begin{align*} \overline{S}(\mathbf{q}^{\sigma}, \omega) &= \max_{i\in\mathcal{I}_1^{\omega}} \frac{ \log P_{0}^{\omega}(i) }{ \log \unicode{x3bb}_{i}^{(\omega_1)} } + \max_{i\in\mathcal{I}_2^{\omega}} \frac{ \log P_{1}^{\omega}(i) }{ \log \unicode{x3bb}_{i}^{(\omega_2)} } \\ &= \max\bigg\{ s\cdot\frac{\log a_1}{\log b_1}, s\cdot\frac{\log a_2}{\log b_2} +r, s \cdot\frac{\log a_2}{\log b_3} +r \bigg\} + 0. \end{align*} $$

The last two terms are at most $s+r$ if and only if $a_2\geqslant \max \{b_2,b_3\}$ and the first term is at most $s+r$ if and only if $b_1^{1+r/s}\leqslant a_1$ , completing the proof.

4.2 Characterization of SPPC in dimension $3$

Recall from Lemma 3.2 that $\mathcal {A}=\mathcal {B}$ in $d=3$ and the notation $y\prec x$ from (3.1). If no coordinate dominates any other, then (recall) F is a genuine Barański sponge and projection to any of the three principal planes is a Barański carpet. For genuine Barański sponges with $d=3$ , it is not necessarily true that $\mathcal {B}=\mathcal {S}_3$ . For example, take an IFS consisting of two maps with $\unicode{x3bb} _1^{(3)}<\unicode{x3bb} _1^{(2)}<\unicode{x3bb} _1^{(1)}$ and $\unicode{x3bb} _2^{(1)}<\unicode{x3bb} _2^{(2)}<\unicode{x3bb} _2^{(3)}$ . Depending on these parameters, only one of the orderings $(1,3,2)$ and $(2,3,1)$ is an element of $\mathcal {B}$ because there is no $\mathbf {p}\in \mathcal {P}_{\mathcal {I}}$ that simultaneously satisfies $\chi _{1}(\mathbf {p}) < \chi _{3}(\mathbf {p}) < \chi _{2}(\mathbf {p})$ and $\chi _{2}(\mathbf {p}) < \chi _{3}(\mathbf {p}) < \chi _{1}(\mathbf {p})$ . BY analogous reasoning, either $(2,1,3)\in \mathcal {B}$ or $(3,1,2)\in \mathcal {B}$ .

Assuming that $y\prec x$ , we have $\mathcal {A}\subseteq \{(x,y,z), (x,z,y), (z,x,y)\}$ . Hence, projection onto the $(y,z)$ -plane never plays a role. If $\#\mathcal {A}=1$ , then F is a Lalley–Gatzouras sponge. There are potentially three possibilities for $\#\mathcal {A}=2$ :

1. (1) $\mathcal {A}=\{(x,y,z),(x,z,y)\}$ , that is, $\max \{y,z\}\prec x$ . In this case, the projections onto both the $(x,y)$ - and $(x,z)$ -planes are Lalley–Gatzouras carpets with x being the dominant side.

2. (2) $\mathcal {A}=\{(x,z,y),(z,x,y)\}$ , that is, $y\prec \min \{x,z\}$ . In this case, projection onto the $(x,z)$ -plane is a Barański carpet and $y\prec \min \{x,z\}$ implies that projection onto either the $(x,y)$ - or $(y,z)$ -plane can be arbitrary.

The third option is not possible due to the following proposition.

Proposition 4.3. Let F be a three-dimensional sponge that satisfies the SPPC, $y\prec x$ and $(x,y,z),(z,x,y)\in \mathcal {A}$ . Then also $(x,z,y)\in \mathcal {A}$ .

Proof. All maps of the IFS defining F cannot be ordered the same way; therefore, without loss of generality we assume that

(4.1) $$ \begin{align} \unicode{x3bb}_1^{(z)} < \unicode{x3bb}_1^{(y)} < \unicode{x3bb}_1^{(x)} \quad\text{and}\quad \unicode{x3bb}_2^{(y)} < \unicode{x3bb}_2^{(x)} < \unicode{x3bb}_2^{(z)} \end{align} $$

corresponding to ordering $(x,y,z)$ and $(z,x,y)$ , respectively. We also assume that $f_1$ and $f_2$ do not overlap exactly on either the $(x,y)$ - or $(x,z)$ -plane.

According to Lemma 3.1 it is enough to show that there exists $\mathbf {p}\in \mathcal {P}_{\mathcal {I}}$ such that $\chi _x(\mathbf {p}) < \chi _{z}(\mathbf {p}) < \chi _{y}(\mathbf {p})$ . Consider $\mathbf {p}=(p,1-p,0,\ldots ,0)$ noting that the calculations that follow can also be adapted to small enough perturbations of $\mathbf {p}$ . Straightforward algebraic manipulations yield

$$ \begin{align*} \chi_x(\mathbf{p}) < \chi_{z}(\mathbf{p})\ {\Longleftrightarrow}\ p>A \quad\text{and}\quad \chi_{z}(\mathbf{p}) < \chi_{y}(\mathbf{p})\ {\Longleftrightarrow}\ p<B, \end{align*} $$

where

$$ \begin{align*} A:= \frac{\log (\unicode{x3bb}_2^{(x)}/\unicode{x3bb}_2^{(z)})}{\log ( (\unicode{x3bb}_2^{(x)}\unicode{x3bb}_1^{(z)}) / (\unicode{x3bb}_2^{(z)}\unicode{x3bb}_1^{(x)}) )} \quad\text{and}\quad B:= \frac{\log (\unicode{x3bb}_2^{(y)}/\unicode{x3bb}_2^{(z)})}{\log ( (\unicode{x3bb}_2^{(y)}\unicode{x3bb}_1^{(z)}) / (\unicode{x3bb}_2^{(z)}\unicode{x3bb}_1^{(y)}) )}. \end{align*} $$

Additional manipulations show $A<B$ if and only if

$$ \begin{align*} \frac{\log (\unicode{x3bb}_1^{(z)}/\unicode{x3bb}_1^{(y)})}{\log ( \unicode{x3bb}_2^{(y)} / \unicode{x3bb}_2^{(z)} )} < \frac{\log (\unicode{x3bb}_1^{(z)}/\unicode{x3bb}_1^{(x)})}{\log ( \unicode{x3bb}_2^{(x)} / \unicode{x3bb}_2^{(z)} )}, \end{align*} $$

which is always true because of (4.1). This completes the proof.

5 Symbolic arguments

In this section we work on the symbolic space $\Sigma = \mathcal {I}^{\mathbb {N}}$ of all one-sided infinite words $\mathbf {i}=i_1,i_2,\ldots $ with the Bernoulli measure $\mu _{\mathbf {p}}=\mathbf {p}^{\mathbb {N}}$ . Recall the notation from §2. Throughout the section a $\sigma $ -order always refers to a cube as defined in (2.4). We define symbolic cubes whose images under the natural projection (1.1) well-approximate Euclidean balls on the sponge F. Let $\Sigma _{r}^{\sigma }:= \{\mathbf {i}\in \Sigma : \mathbf {i} \text { is } \sigma \text {-ordered at scale } r\}$ . We define the $\sigma $ -ordered symbolic r-approximate cube containing $\mathbf {i}\in \Sigma _{r}^{\sigma }$ to be

(5.1) $$ \begin{align} B_{\mathbf{i}}(r):= \{\mathbf{j} \in \Sigma: |\Pi_{n}^{\sigma} \mathbf{j} \wedge \Pi_{n}^{\sigma} \mathbf{i}| \geqslant L_{\mathbf{i}}(r, \sigma_{n}) \text { for every } 1 \leqslant n \leqslant d\}, \end{align} $$

where $\mathbf {i}\wedge \mathbf {j}$ denotes the longest common prefix of $\mathbf {i}$ and $\mathbf {j}$ . This is the natural extension of the notion of approximate squares used extensively in the study of planar carpets. Due to (2.2), the image $\pi (B_{\mathbf {i}}(r))$ is contained within a hypercuboid of $[0,1]^d$ aligned with the coordinate axes with side lengths at most r. Observe that if $\mathbf {i}\in \Sigma _{r}^{\sigma }$ , then for all $\mathbf {j}\in B_{\mathbf {i}}(r)$ also $\mathbf {j}\in \Sigma _{r}^{\sigma }$ . Thus, we identify the $\sigma $ -ordering of $B_{\mathbf {i}}(r)$ with the $\sigma $ -ordering of $\mathbf {i}$ at scale r. If $\mathbf {i}\in \Sigma _{r}^{\sigma }$ , then the surjectivity of the maps $\Pi _n^{\sigma }$ implies that $B_{\mathbf {i}}(r)$ can be identified with a sequence of symbols of length $L_{\mathbf {i}}(r,\sigma _1)$ of the form

where we set $L_{\mathbf {i}}(r,\sigma _{d+1}):= 0$ .

The following lemmas collect important properties about the $\mu _{\mathbf {p}}$ measure of a symbolic r-approximate cube. The first is the extension of [21, equation (6.2)]. We use the convention that any empty product is equal to $1$ .

Lemma 5.1. The $\mu _{\mathbf {p}}$ measure of a $\sigma $ -ordered symbolic r-approximate cube is equal to

$$ \begin{align*} \mu_{\mathbf{p}}(B_{\mathbf{i}}(r)) = \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(r,\sigma_{n+1})+1}^{L_{\mathbf{i}}(r,\sigma_n)} p_n^{\sigma}(\Pi_n^{\sigma}i_{\ell}) = \prod_{n=1}^{d} \prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_n)} P_{n-1}^{\sigma}(\Pi_{n}^{\sigma} i_{\ell}). \end{align*} $$

Proof. From definition (5.1) of $B_{\mathbf {i}}(r)$ it follows that an approximate cube is the disjoint union of level- $L_{\mathbf {i}}(r,\sigma _1)$ cylinder sets:

$$ \begin{align*} \{ [j_1,\ldots,j_{L_{\mathbf{i}}(r,\sigma_1)}]: \Pi_{n}^{\sigma} j_{\ell}&=\Pi_n^{\sigma} i_{\ell} \text{ for } \ell=L_{\mathbf{i}}(r,\sigma_{n+1})\\&\quad+1,\ldots,L_{\mathbf{i}}(r,\sigma_n) \text{ and } 1\leqslant n\leqslant d \}. \end{align*} $$

For each such cylinder, $\mu _{\mathbf {p}}([j_1,\ldots ,j_{L_{\mathbf {i}}(r,\sigma _1)}]) = \prod _{\ell =1}^{L_{\mathbf {i}}(r,\sigma _1)} p(j_{\ell })$ . Summing and using multiplicativity, we obtain

$$ \begin{align*} \mu_{\mathbf{p}}(B_{\mathbf{i}}(r)) = \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(r,\sigma_{n+1})+1}^{L_{\mathbf{i}}(r,\sigma_n)}\, \sum_{j\in\mathcal{I}: \Pi_n^{\sigma} j=\Pi_n^{\sigma} i_{\ell}} p(j) = \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(r,\sigma_{n+1})+1}^{L_{\mathbf{i}}(r,\sigma_n)}\, p_n^{\sigma}(\Pi_n^{\sigma} i_{\ell}). \end{align*} $$

The last equality in the assertion follows from definition (2.10) of $P_{n-1}^{\sigma }(\Pi _{n}^{\sigma } i_{\ell })$ .

Remark 5.2. Assume $B_{\mathbf {i}}(r)$ is $\sigma $ -ordered and $L_{\mathbf {i}}(r,\sigma _m)=L_{\mathbf {i}}(r,\sigma _{m-1})=\cdots =L_{\mathbf {i}}(r,\sigma _{m-k})$ for some $1\leqslant k< m\leqslant d$ . Then the formula for $\mu _{\mathbf {p}}(B_{\mathbf {i}}(r))$ can also be calculated using the ordering $(\sigma _1,\ldots ,\sigma _{m-k-1},\omega ,\sigma _{m+1},\ldots ,\sigma _d)$ , where the first block is empty if $k=m-1$ , the last block is empty if $m=d$ and $\omega $ is any permutation of $\sigma _m,\sigma _{m-1},\ldots ,\sigma _{m-k}$ .

Motivated by the definition of $\dim _{\mathrm {A}}\nu $ , the goal is to bound the ratio $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R))/\mu _{\mathbf {p}}(B_{\mathbf {i}}(r))$ for approximate cubes with different orderings. The first step is to consider when $B_{\mathbf {i}}(R)$ and $B_{\mathbf {i}}(r)$ have the same ordering.

Let $\unicode{x3bb} _{\min }:= \min _{n,i} \unicode{x3bb} _i^{(n)}$ and fix $\sigma \in \mathcal {A}$ . For $1\leqslant n\leqslant d$ , we introduce

(5.2) $$ \begin{align} \overline{k}_n^{\sigma} := \operatorname*{\mbox{arg max}}_{i\in\mathcal{I}_n^{\sigma}} \frac{ \log P_{n-1}^{\sigma}(i) }{ \log \unicode{x3bb}_{i}^{(\sigma_n)} },\quad \underline{k}_n^{\sigma} := \operatorname*{\mbox{arg min}}_{i\in\mathcal{I}_n^{\sigma}} \frac{ \log P_{n-1}^{\sigma}(i) }{ \log \unicode{x3bb}_{i}^{(\sigma_n)} } \end{align} $$

and

(5.3) $$ \begin{align} \overline{s}_n^{\sigma} := \frac{ \log P_{n-1}^{\sigma}(\overline{k}_n^{\sigma}) }{ \log \unicode{x3bb}_{\overline{k}_n^{\sigma}}^{(\sigma_n)} },\quad \underline{s}_n^{\sigma} := \frac{ \log P^\sigma_{n-1}(\underline{k}_n^{\sigma}) }{ \log \unicode{x3bb}_{\underline{k}_n^{\sigma}}^{(\sigma_n)} }. \end{align} $$

With this notation $\overline {S}(\mathbf {p},\sigma ) = \sum _{n=1}^d \overline {s}_n^{\sigma }$ and $\underline {S}(\mathbf {p},\sigma ) = \sum _{n=1}^d \underline {s}_n^{\sigma }$ . If there are multiple choices for either $\overline {k}_n^{\sigma }$ or $\underline {k}_n^{\sigma }$ , then choose one arbitrarily.

Lemma 5.3. Fix $\sigma \in \mathcal {A}$ and assume that both $B_{\mathbf {i}}(R)$ and $B_{\mathbf {i}}(r)$ are $\sigma $ -ordered, where $0<R\leqslant 1$ and $r<\unicode{x3bb} _{\min } R$ . Then there exists a constant $C>1$ depending only on the sponge F such that

$$ \begin{align*} C^{-1} \bigg( \frac{R}{r} \bigg)^{ \underline{S}(\mathbf{p},\sigma) } \leqslant \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} \leqslant C \bigg( \frac{R}{r} \bigg)^{ \overline{S}(\mathbf{p},\sigma) }. \end{align*} $$

Proof. It follows from Lemma 5.1 that

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} &= \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(R,\sigma_n)+1}^{L_{\mathbf{i}}(r,\sigma_n)} \frac{1}{P_{n-1}^{\sigma}(\Pi_{n}^{\sigma}i_{\ell})}\\ &= \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(R,\sigma_n)+1}^{L_{\mathbf{i}}(r,\sigma_n)} ( \unicode{x3bb}_{\Pi_n^\sigma i_{\ell}}^{(\sigma_n)} )^{{\log P_{n-1}^{\sigma}(\Pi_{n}^{\sigma}i_{\ell})}/{-\!\log \unicode{x3bb}_{\Pi_n^{\sigma} i_{\ell}}^{(\sigma_n)} }}. \end{align*} $$

The requirement that $r<\unicode{x3bb} _{\min } R$ ensures that $L_{\mathbf {i}}(R,\sigma _n)<L_{\mathbf {i}}(r,\sigma _n)$ for all n. We bound each exponent individually to obtain

(5.4) $$ \begin{align} \prod_{n=1}^{d} \bigg( \prod_{\ell=L_{\mathbf{i}}(R,\sigma_n)+1}^{L_{\mathbf{i}}(r,\sigma_n)} \unicode{x3bb}_{\Pi_n^{\sigma} i_{\ell}}^{(\sigma_n)} \bigg)^{ -\underline{s}_n^{\sigma} } \leqslant \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} \leqslant \prod_{n=1}^{d} \bigg( \prod_{\ell=L_{\mathbf{i}}(R,\sigma_n)+1}^{L_{\mathbf{i}}(r,\sigma_n)} \unicode{x3bb}_{\Pi_n^{\sigma} i_{\ell}}^{(\sigma_n)} \bigg)^{ -\overline{s}_n^{\sigma} }. \end{align} $$

From definition (2.2) of $L_{\mathbf {i}}(r,n)$ it follows that there exists $C>1$ such that

(5.5) $$ \begin{align} C^{-1} \cdot\frac{r}{R}\leqslant \prod_{\ell=L_{\mathbf{i}}(R,n)+1}^{L_{\mathbf{i}}(r,n)} \unicode{x3bb}_{i_{\ell}}^{(n)} \leqslant C\cdot \frac{r}{R}, \end{align} $$

which together with (5.4) concludes the proof.

Now we extend Lemma 5.3 so that $B_{\mathbf {i}}(R)$ and $B_{\mathbf {i}}(r)$ can have different orderings. This step, which represents one of the key technical challenges in the paper, is not necessary if F is a Lalley–Gatzouras sponge.

Proposition 5.4. Assume $0<R\leqslant 1$ and $r<\unicode{x3bb} _{\min } R$ . Then there exists a constant $C>1$ depending only on the sponge F such that

$$ \begin{align*} C^{-1} \bigg( \frac{R}{r} \bigg)^{ \min_{\sigma\in\mathcal{A}} \underline{S}(\mathbf{p},\sigma) } \leqslant \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} \leqslant C \bigg( \frac{R}{r} \bigg)^{ \max_{\sigma\in\mathcal{A}} \overline{S}(\mathbf{p},\sigma) }. \end{align*} $$

5.1 Proof of Proposition 5.4

Let $\sigma _{\mathbf {i}}(r)$ denote the ordering of $B_{\mathbf {i}}(r)$ and assume $\sigma _{\mathbf {i}}(R)\neq \sigma _{\mathbf {i}}(r)$ . Trying to estimate the ratio $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R))/\mu _{\mathbf {p}}(B_{\mathbf {i}}(r))$ directly using Lemma 5.1 did not lead us to a proof. Instead, the rough idea is to divide the interval $[r,R]$ of scales into a uniformly bounded number of subintervals so that the ordering at roughly the two endpoints of a subinterval is the same. Then we repeatedly apply Lemma 5.3 to each subinterval. The next lemma allows us to make a subdivision.

Lemma 5.5. Fix $\varepsilon>0$ such that $1-\varepsilon> \max _{n,i} \unicode{x3bb} _i^{(n)}$ . There exists a constant $C_1=C_1(F,\mathbf {p},\varepsilon )<\infty $ such that for all $\mathbf {i}\in \Sigma $ and $0<R\leqslant 1$ ,

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}((1-\varepsilon)R))} \leqslant C_1. \end{align*} $$

Proof. First assume that $\sigma _{\mathbf {i}}(R)= \sigma _{\mathbf {i}}((1-\varepsilon )R)=\sigma $ and consider the symbolic representation of $B_{\mathbf {i}}(R)$ and $B_{\mathbf {i}}((1-\varepsilon )R)$ . They could be different at indices

$$ \begin{align*} L_{\mathbf{i}}(R,\sigma_n)+1,\ldots, L_{\mathbf{i}}(R,\sigma_n)+ d-n+1 \quad\text{for each } 1\leqslant n\leqslant d, \end{align*} $$

but necessarily agree at all other indices due to the choice of $\varepsilon $ . Where they agree, the corresponding terms simply cancel out in $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R)) / \mu _{\mathbf {p}}(B_{\mathbf {i}}((1-\varepsilon )R))$ . Hence, there are at most $1+2+\cdots +d<d^2$ different indices of interest. An index where they differ corresponds in $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R)) / \mu _{\mathbf {p}}(B_{\mathbf {i}}((1-\varepsilon )R))$ to a ratio $p/q$ , where $p\geqslant q$ (p is a sum containing q by (2.9)) and both $p,q$ are uniformly bounded away from $0$ (simply because p and q are sums of different terms of $\mathbf {p}$ which all are strictly positive to begin with). Therefore, there exists a uniform upper bound C for $p/q$ . As a result,

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}((1-\varepsilon)R))} \leqslant C^{d^2}, \end{align*} $$

completing the proof in this case by setting $C_1=C^{d^2}$ .

We claim that even if $\sigma _{\mathbf {i}}(R)\neq \sigma _{\mathbf {i}}((1-\varepsilon )R)$ , there still exists an ordering $\omega $ such that the value of $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R))$ is the same when calculating it with $\sigma _{\mathbf {i}}(R)$ or $\omega $ , and likewise the value of $\mu _{\mathbf {p}}(B_{\mathbf {i}}((1-\varepsilon )R))$ is the same when calculating it with $\sigma _{\mathbf {i}}((1-\varepsilon )R)$ or $\omega $ . Hence, we may apply the previous argument to $\omega $ .

To see the claim, first observe that the ordering $\sigma _{\mathbf {i}}(R)=\sigma $ can be partitioned into $1\leqslant K\leqslant d$ blocks along indices $d\geqslant n_1>n_2>\cdots >n_K=1$ so that

$$ \begin{align*} L_{\mathbf{i}}(R,\sigma_d) = \cdots = L_{\mathbf{i}}(R,\sigma_{n_1}) < L_{\mathbf{i}}(R,&\sigma_{n_1+1}) = \cdots = L_{\mathbf{i}}(R,\sigma_{n_2}) \\ &\quad <\cdots< L_{\mathbf{i}}(R,\sigma_{n_{K-1}+1}) = \cdots = L_{\mathbf{i}}(R,\sigma_{n_K}). \end{align*} $$

The assumption on $\varepsilon $ implies that $L_{\mathbf {i}}((1\kern-1pt -\varepsilon )R,n)-L_{\mathbf {i}}(R,n)\kern-1pt\in\kern-1pt \{0,\kern-1pt 1\}$ for all coordinates n. Therefore, we can partition the block $X_{\ell }:= \{\sigma _{n_{\ell }},\ldots ,\sigma _{n_{\ell -1}+1}\}$ into $Y_{\ell }\sqcup Z_{\ell }$ , where $Y_{\ell }=\{n\in X_{\ell }: L_{\mathbf {i}}((1-\varepsilon )R,n)=L_{\mathbf {i}}(R,n)\}$ and $Z_{\ell }=\{n\in X_{\ell }: L_{\mathbf {i}}((1-\varepsilon )R,n)=L_{\mathbf {i}}(R,n)+1\}$ . We fix an (arbitrary) ordering of all $Y_{\ell }$ , $Z_{\ell }$ and define

$$ \begin{align*} \omega:= (Z_K,Y_K,Z_{K-1},Y_{K-1},\ldots,Z_2,Y_2,Z_1,Y_1). \end{align*} $$

By Remark 5.2, $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R))$ can be calculated by another ordering that only permutes elements within any of the blocks $X_{\ell }$ . The ordering $\omega $ clearly satisfies this. It remains to argue that $\omega $ also works for $\sigma _{\mathbf {i}}((1-\varepsilon )R)$ .

If $n\in Y_{\ell }$ and $m\in Z_\ell $ (for some $1\leqslant \ell \leqslant K$ ) then by definition $L_{\mathbf {i}}((1-\varepsilon )R,n) < L_{\mathbf {i}}((1-\varepsilon )R,m)$ . Moreover, If $n\in Z_{\ell }$ and $m\in Y_{\ell +1}$ (for some $1\leqslant \ell \leqslant K-1$ ) then we also have $L_{\mathbf {i}}((1-\varepsilon )R,n) \leqslant L_{\mathbf {i}}((1-\varepsilon )R,m)$ . These imply that $\sigma _{\mathbf {i}}((1-\varepsilon )R)$ can be obtained from $\omega $ by only permuting elements within a block $Y_{\ell }$ or $Z_{\ell }$ . This exactly means that $\mu _{\mathbf {p}}(B_{\mathbf {i}}((1-\varepsilon )R))$ can be calculated using $\omega $ .

We next define the scales where we subdivide $[r,R]$ . Let

$$ \begin{align*} R_1:= \inf\{ r'>r: \sigma_{\mathbf{i}}(r')=\sigma_{\mathbf{i}}(R) \} \end{align*} $$

and terminate if $\sigma _{\mathbf {i}}((1-\varepsilon )R_{1})=\sigma _{\mathbf {i}}(r)$ , otherwise, for $k\geqslant 2$ until $\sigma _{\mathbf {i}}((1-\varepsilon )R_{k})=\sigma _{\mathbf {i}}(r)$ define

$$ \begin{align*} R_k:= \inf\{ r'>r: \sigma_{\mathbf{i}}(r') = \sigma_{\mathbf{i}}((1-\varepsilon)R_{k-1}) \} \end{align*} $$

concluding with $R_M$ , where $\varepsilon =\varepsilon (r)>0$ is chosen so small that $1-\varepsilon > \max \{r/R_M, \max _{n,i} \unicode{x3bb} _i^{(n)}\}$ . It follows from the construction that $\sigma _{\mathbf {i}}((1-\varepsilon )R_{k})$ is always different from the previous orderings, hence $M\leqslant d!$ .

We are ready to conclude the proof. We suppress multiplicative constants c depending only on F by writing $X\lesssim Y$ if $X\leqslant cY$ . Using first Lemma 5.5 and then Lemma 5.3, we get the upper bound

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} &\lesssim \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R_1))} \cdot \prod_{k=2}^M \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}((1-\varepsilon)R_{k-1}))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R_k))} \cdot \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}((1-\varepsilon)R_M))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} \\ &\lesssim \bigg( \frac{R}{R_1} \bigg)^{ \overline{S}(\mathbf{p},\sigma_{\mathbf{i}}(R_1)) } \prod_{k=2}^M \bigg( \frac{(1-\varepsilon)R_{k-1}}{R_k} \bigg)^{ \overline{S}(\mathbf{p},\sigma_{\mathbf{i}}(R_k)) } \bigg( \frac{(1-\varepsilon)R_M}{r} \bigg)^{ \overline{S}(\mathbf{p},\sigma_{\mathbf{i}}(r)) } \\ &\lesssim \bigg( \frac{R}{r} \bigg)^{ \max_{\sigma\in\mathcal{A}} \overline{S}(\mathbf{p},\sigma) }. \end{align*} $$

The lower bound is very similar. Lemma 5.5 is not necessary because $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R)) \geqslant \mu _{\mathbf {p}}(B_{\mathbf {i}}((1-\varepsilon )R))$ holds for any $R>0$ and one uses $\min _{\sigma \in \mathcal {A}} \underline {S}(\mathbf {p},\sigma )$ instead in the last step. The proof of Proposition 5.4 is complete.

6 Proof of Theorem 2.5

6.1 Transferring symbolic estimates to geometric estimates

The very strong SPPC implies that there exists $\delta _0>0$ depending only on the sponge F such that for every $\sigma \in \mathcal {A}$ , $1\leqslant n\leqslant d$ and $i,j\in \mathcal {I}$ for which $f_i$ and $f_j$ do not overlap exactly on $E_n^{\sigma }$ ,

$$ \begin{align*} \mathrm{dist}( \Pi_n^{\sigma}(f_i([0,1]^d)), \Pi_n^{\sigma}(f_j([0,1]^d)) ) \geqslant \delta_0. \end{align*} $$

The next lemma allows us to replace a Euclidean ball $B(x,r)$ with the image of an approximate cube of roughly the same diameter under the natural projection $\pi $ ; recall (1.1). It is an adaptation of [21, Proposition 6.2.1]. The short proof is included for completeness.

Lemma 6.1. Assume the sponge F satisfies the SPPC. For all $\mathbf {i}\in \Sigma $ and $r>0$ ,

$$ \begin{align*} \pi(B_{\mathbf{i}}(r)) \subseteq B(\pi(\mathbf{i}),\sqrt{d}\cdot r). \end{align*} $$

Moreover, if F satisfies the very strong SPPC, then

$$ \begin{align*} B(\pi(\mathbf{i}), \delta_0 \cdot r)\cap F \subseteq \pi(B_{\mathbf{i}}(r)). \end{align*} $$

Proof. By definition (5.1), the image $\pi (B_{\mathbf {i}}(r))$ is contained inside a cuboid of side length $\prod _{\ell =1}^{L_{\mathbf {i}}(r,n)} \unicode{x3bb} _{i_\ell }^{(n)} \leqslant r$ in each coordinate n. In the worst case, $\pi (\mathbf {i})$ is a corner of this cuboid which is then certainly contained in $B(\pi (\mathbf {i}),\sqrt {d}\cdot r)$ .

We show that $\mathbf {j}\notin B_{\mathbf {i}}(r)$ implies $\pi (\mathbf {j})\notin B(\pi (\mathbf {i}), \delta _0 \cdot r)$ under the very strong SPPC. Assume $B_{\mathbf {i}}(r)$ is $\sigma $ -ordered. Since $\mathbf {j}\notin B_{\mathbf {i}}(r)$ , there exist a largest $n'\in \{1,\ldots ,d\}$ and a smallest $\ell '\in \{L_{\mathbf {i}}(r,\sigma _{n'+1})+1,\ldots ,L_{\mathbf {i}}(r,\sigma _{n'})\}$ such that $\Pi _{n'}^{\sigma }j_{\ell '}\neq \Pi _{n'}^{\sigma }i_{\ell '}$ . For this particular choice, the very strong SPPC implies that

$$ \begin{align*} \mathrm{dist}( \Pi_{n'}^{\sigma}(f_{i_{\ell'}}([0,1]^d)), \Pi_{n'}^{\sigma}(f_{j_{\ell'}}([0,1]^d)) ) \geqslant \delta_0. \end{align*} $$

Since the projection $\Pi _{n'}^{\sigma }$ can only decrease distance and $\Pi _{n'}^{\sigma }j_{\ell }= \Pi _{n'}^{\sigma }i_{\ell }$ for all $\ell <\ell '$ , we can bound

$$ \begin{align*} \mathrm{dist}(\pi(\mathbf{i}),\pi(\mathbf{j})) &\geqslant \mathrm{dist}(\Pi_{n'}^{\sigma}(\pi(\mathbf{i})),\Pi_{n'}^{\sigma}(\pi(\mathbf{j}))) \\ &\geqslant \mathrm{dist}(\Pi_{n'}^{\sigma}(f_{i_1\ldots i_{\ell'-1}i_{\ell'}}([0,1]^d)), \Pi_{n'}^{\sigma}(f_{j_1\ldots j_{\ell'-1}j_{\ell'}}([0,1]^d))) \\ &\geqslant \delta_0\cdot \prod_{\ell=1}^{\ell'-1} \unicode{x3bb}_{i_\ell}^{(\sigma_{n'})} \\ &\stackrel{(2.2)}{>} \delta_0\cdot r, \end{align*} $$

completing the proof.

The very strong SPPC also implies that the natural projection $\pi $ is injective and that $\mu _{\mathbf {p}}(B_{\mathbf {i}}(r))=\nu _{\mathbf {p}}(\pi (B_{\mathbf {i}}(r)))$ for any approximate cube $B_{\mathbf {i}}(r)$ . This, together with Lemma 6.1, implies that for any $\mathbf {i}\in \Sigma $ and $0<r<R\leqslant 1$ ,

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R/\sqrt{d}))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r/\delta_0))} \leqslant \frac{\nu_{\mathbf{p}}(B(\pi(\mathbf{i}),R))}{\nu_{\mathbf{p}}(B(\pi(\mathbf{i}),r))} \leqslant \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R/\delta_0))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r/\sqrt{d}))}. \end{align*} $$

Hence, it is enough to consider the ratio $\mu _{\mathbf {p}}(B_{\mathbf {i}}(R))/\mu _{\mathbf {p}}(B_{\mathbf {i}}(r))$ .

The upper bound for $\dim _{\mathrm {A}}\nu _{\mathbf {p}}$ and the lower bound for $\dim _{\mathrm {L}}\nu _{\mathbf {p}}$ now directly follow from Proposition 5.4. The lower bound for $\dim _{\mathrm {A}}\nu _{\mathbf {p}}$ requires more work and we give the argument in the next subsection. The argument for the upper bound for $\dim _{\mathrm {L}}\nu _{\mathbf {p}}$ is analogous and we omit the details.

6.2 Lower bound for Assouad dimension

Recall the notation from (5.2) and (5.3). Using Lemma 6.1, in order to bound $\dim _{\mathrm {A}}\nu _{\mathbf {p}}$ from below, it suffices to prove the following proposition.

Proposition 6.2. For all $\sigma \in \mathcal {B}$ , there exists a sequence of triples $(R, r, \mathbf {i}) \in (0,1) \times (0,1) \times \Sigma $ with $R/r\to \infty $ such that

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} \geqslant c \bigg( \frac{R}{r} \bigg)^{ \overline{S}(\mathbf{p},\sigma) } \end{align*} $$

for some constant $c>0$ uniformly for all triples in the sequence.

Proof. Fix $\sigma \in \mathcal {B}$ . By definition of $\mathcal {B}$ , there exist $\mathbf {j} \in \Sigma $ and $\rho>0$ such that $\mathbf {j}$ determines a strictly $\sigma $ -ordered cylinder at scale $\rho $ ; see (2.3). By passing to a finite iterate of the original IFS if necessary, we may assume that $L_{\mathbf {j}}(\rho ,\sigma _d) = 1$ . Therefore, there exists $j \in \mathcal {I}$ with

$$ \begin{align*} \unicode{x3bb}_{j}^{(\sigma_d)} < \unicode{x3bb}_{j}^{(\sigma_{d-1})} < \cdots < \unicode{x3bb}_{j}^{(\sigma_1)}. \end{align*} $$

We use this j together with $\overline {k}^\sigma _n$ ( $n=1, \ldots , d)$ (see (5.2)) to build the $\mathbf {i}\in \Sigma $ from the statement of the proposition. We now construct the sequence of triples $(R,r,\mathbf {i})$ . This is done by first choosing a decreasing sequence of R tending to 0 with the first term sufficiently small. For a particular R the associated r and $\mathbf {i}$ are built as follows. First, for $a,b \in \{1, \ldots , d\}$ and $v \in \mathcal {I}$ , write

(6.1) $$ \begin{align} \theta_{b}^{a}(v) = \frac{\log \unicode{x3bb}_v^{(a)}}{\log \unicode{x3bb}_v^{(b)}}>0. \end{align} $$

Observe that

(6.2) $$ \begin{align} \theta_{\sigma_{n}}^{\sigma_{n-1}}(j) < 1 \end{align} $$

for all $n=2, \ldots , d$ . Choose r to satisfy

(6.3) $$ \begin{align} \max_{v \in \mathcal{I}, n=2, \ldots, d} \frac{R^{1+({1-\theta_{\sigma_{n}}^{\sigma_{n-1}}(j)})/{\sum_{\ell=d}^n\theta_{\sigma_{\ell}}^{\sigma_{n-1}}(v) }}}{\unicode{x3bb}_{\min}^{1+{\theta_{\sigma_{n}}^{\sigma_{n-1}}(j)}/{\sum_{\ell=d}^n\theta_{\sigma_{\ell}}^{\sigma_{n-1}}(v) }}} < r< \unicode{x3bb}_{\min} R. \end{align} $$

Choosing r in the range (6.3) is possible for sufficiently small R since the bound on the left is $o(R)$ as $R \to 0$ due to (6.2). Moreover, this allows the choice to be made while also ensuring $R/r\to \infty $ . Let $\mathbf {i} = i_1, i_2, \ldots \in \Sigma $ be such that

$$ \begin{align*} i_{\ell} = \overline{k}^\sigma_n \end{align*} $$

for $\ell =L_{\mathbf {i}}(R,\sigma _n)+1, \ldots , L_{\mathbf {i}}(r,\sigma _n)$ and all other entries are j. Note that the upper bound from (6.3) immediately guarantees

$$ \begin{align*} L_{\mathbf{i}}(R,\sigma_n)<L_{\mathbf{i}}(r,\sigma_n) \end{align*} $$

for all $n=1, \ldots , d$ . In order to show that $\mathbf {i}$ is indeed well defined, we claim that the lower bound from (6.3) guarantees

(6.4) $$ \begin{align} L_{\mathbf{i}}(r,\sigma_n)<L_{\mathbf{i}}(R,\sigma_{n-1}) \end{align} $$

for $n=2, \ldots , d+1$ , where we adopt the convention that $L_{\mathbf {i}}(r,\sigma _{d+1})= 0$ . This takes more work. Proceeding by (backwards) induction, let $n \in \{2, \ldots , d\}$ and assume that (6.4) holds for $ n+1, \ldots , d+1$ . The goal is to establish (6.4) for n. By definition of $L_{\mathbf {i}}(R, \sigma _{n-1})$ (see (2.2)),

$$ \begin{align*} \unicode{x3bb}_{\min} R < \prod_{\ell=1}^{L_{\mathbf{i}}(R, \sigma_{n-1})} \unicode{x3bb}_{i_{\ell}}^{( \sigma_{n-1})} \leqslant R, \end{align*} $$

and therefore (6.4) will hold provided

$$ \begin{align*} \Lambda:= \prod_{\ell=1}^{L_{\mathbf{i}}(r, \sigma_{n})} \unicode{x3bb}_{i_{\ell}}^{( \sigma_{n-1})}> R. \end{align*} $$

By the inductive hypothesis and construction of $\mathbf {i}$ ,

$$ \begin{align*} \Lambda = \prod_{\ell=d}^n (\unicode{x3bb}_{j}^{( \sigma_{n-1})} )^{L_{\mathbf{i}}(R,\sigma_{\ell}) - L_{\mathbf{i}}(r,\sigma_{\ell+1}) } (\unicode{x3bb}_{\overline{k}^\sigma_{\ell}}^{ (\sigma_{n-1})} )^{L_{\mathbf{i}}(r,\sigma_{\ell}) - L_{\mathbf{i}}(R,\sigma_{\ell}) }, \end{align*} $$

where we have changed the use of the index $\ell $ slightly. Invoking (6.1) and using (2.2),

$$ \begin{align*} \Lambda &= \prod_{\ell=d}^n (\unicode{x3bb}_{j}^{( \sigma_{n})} )^{\theta_{\sigma_{n}}^{\sigma_{n-1}}(j) (L_{\mathbf{i}}(R,\sigma_{\ell}) - L_{\mathbf{i}}(r,\sigma_{\ell+1})) } (\unicode{x3bb}_{\overline{k}^\sigma_{\ell}}^{ (\sigma_{\ell})} )^{\theta_{\sigma_{\ell}}^{\sigma_{n-1}}(\overline{k}^\sigma_{\ell}) (L_{\mathbf{i}}(r,\sigma_{\ell}) - L_{\mathbf{i}}(R,\sigma_{\ell})) } \\ &= \bigg(\prod_{\ell=d}^n (\unicode{x3bb}_{j}^{( \sigma_{n})} )^{L_{\mathbf{i}}(R,\sigma_\ell) - L_{\mathbf{i}}(r,\sigma_{\ell+1}) } \bigg)^{\theta_{\sigma_{n}}^{\sigma_{n-1}}(j)} \prod_{\ell=d}^n \bigg( \frac{\prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_{\ell})} \unicode{x3bb}_{i_{\ell}}^{(\sigma_{n-1})}}{\prod_{\ell=1}^{ L_{\mathbf{i}}(R,\sigma_{\ell})} \unicode{x3bb}_{i_{\ell}}^{(\sigma_{n-1})}} \bigg)^{\theta_{\sigma_{\ell}}^{\sigma_{n-1}}(\overline{k}^\sigma_{\ell}) } \\ &\geqslant \bigg(\prod_{\ell=1}^{L_{\mathbf{i}}(R,\sigma_n)} \unicode{x3bb}_{i_{\ell}}^{(\sigma_n)} \bigg)^{\theta_{\sigma_{n}}^{\sigma_{n-1}}(j)}\prod_{\ell=d}^n \bigg(\frac{\unicode{x3bb}_{\min}r}{R} \bigg)^{\theta_{\sigma_{\ell}}^{\sigma_{n-1}}(\overline{k}^\sigma_{\ell}) } \\ &\geqslant (\unicode{x3bb}_{\min}R)^{\theta_{\sigma_{n}}^{\sigma_{n-1}}(j)} \bigg(\unicode{x3bb}_{\min} \frac{r}{R} \bigg)^{\sum_{\ell=d}^n\theta_{\sigma_{\ell}}^{\sigma_{n-1}}(\overline{k}^\sigma_{\ell}) } \\ &>R \end{align*} $$

by (6.3), which proves (6.4). With the sequence now in place, the result follows easily. For all triples $(R,r,\mathbf {i})$ in the sequence, Lemma 5.1 gives

$$ \begin{align*} \frac{\mu_{\mathbf{p}}(B_{\mathbf{i}}(R))}{\mu_{\mathbf{p}}(B_{\mathbf{i}}(r))} &= \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(R,\sigma_n)+1}^{L_{\mathbf{i}}(r,\sigma_n)} \frac{1}{P_{n-1}^{\sigma}( i_{\ell})} \\ &= \prod_{n=1}^{d}\, \prod_{\ell=L_{\mathbf{i}}(R,\sigma_n)+1}^{L_{\mathbf{i}}(r,\sigma_n)} ( \unicode{x3bb}_{ i_{\ell}}^{(\sigma_n)} )^{-\overline{s}_n^\sigma} \quad (\text{by construction of}\ \mathbf{i})\\ &= \prod_{n=1}^{d}\, \bigg( \frac{\prod_{\ell=1}^{L_{\mathbf{i}}(r,\sigma_n)} \unicode{x3bb}_{ i_{\ell}}^{(\sigma_n)} } {\prod_{\ell=1}^{L_{\mathbf{i}}(R,\sigma_n)} \unicode{x3bb}_{ i_{\ell}}^{(\sigma_n)} } \bigg)^{-\overline{s}_n^\sigma}\\ &\geqslant \prod_{n=1}^{d}\, \bigg( \frac{\unicode{x3bb}_{\min} R}{r} \bigg)^{\overline{s}_n^\sigma} \\ & = \unicode{x3bb}_{\min}^{ \overline{S}(\mathbf{p},\sigma)} \bigg( \frac{R}{r} \bigg)^{ \overline{S}(\mathbf{p},\sigma) } \end{align*} $$

as required.

6.3 Final claim for $\sigma $ -ordered coordinatewise natural measures

The claim for the $\sigma $ -ordered coordinatewise natural measure $\mathbf {q}^{\sigma }$ follows from the simple observation that

$$ \begin{align*} Q_{n-1}^{\sigma}(\Pi_{n}^{\sigma}i) = \frac{q_n^{\sigma}(\Pi_n^{\sigma} i)}{q_{n-1}^{\sigma}(\Pi_{n-1}^{\sigma} i)} = \frac{ \prod_{m=1}^n ( \unicode{x3bb}_{\Pi_m^{\sigma} i}^{(\sigma_m)} )^{s_{m-1}^{\sigma}(\Pi_{m-1}^{\sigma} i)} }{ \prod_{m=1}^{n-1} ( \unicode{x3bb}_{\Pi_m^{\sigma} i}^{(\sigma_m)} )^{s_{m-1}^{\sigma}(\Pi_{m-1}^{\sigma} i)} } = ( \unicode{x3bb}_{\Pi_n^{\sigma} i}^{(\sigma_n)} )^{s_{n-1}^{\sigma}(\Pi_{n-1}^{\sigma} i)}. \end{align*} $$

Hence,

$$ \begin{align*} \frac{ \log Q_{n-1}^{\sigma}(i) }{ \log \unicode{x3bb}_{i}^{(\sigma_n)} } = s_{n-1}^{\sigma}(\Pi_{n-1}^{\sigma}i) \quad\text{for every } i\in\mathcal{I}_n^{\sigma} \text{ and } 1\leqslant n\leqslant d, \end{align*} $$

completing the proof of the claim.