Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T07:16:49.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Attractors associated to a family of hyperbolic 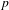$p$-adic plane automorphisms

Part of: Algebraic number theory: local and $p$-adic fields Complex dynamical systems Dynamical systems with hyperbolic behavior Topological dynamics Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  20 February 2020

CLAYTON PETSCHE
CLAYTON PETSCHE*
Affiliation:
Department of Mathematics, Oregon State University, Corvallis, OR97331, USA email petschec@math.oregonstate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a certain two-parameter family of automorphisms of the affine plane over a complete, locally compact non-Archimedean field. Each of these automorphisms admits a chaotic attractor on which it is topologically conjugate to a full two-sided shift map, and the attractor supports a unit Borel measure which describes the distribution of the forward orbit of Haar-almost all points in the basin of attraction. We also compute the Hausdorff dimension of the attractor, which is non-integral.

Keywords

p-adic or non-Archimedean dynamical systemsstrange attractorssymbolic dynamicsphysical measuresHausdorff dimension

MSC classification

Primary: 37P20: Non-Archimedean local ground fields
Secondary: 37D45: Strange attractors, chaotic dynamics 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.) 37B10: Symbolic dynamics 37F35: Conformal densities and Hausdorff dimension 11S82: Non-Archimedean dynamical systems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 6 , June 2021 , pp. 1867 - 1882
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, K., DeMark, D. and Petsche, C.. Non-Archimedean Hénon maps, attractors, and horseshoes. Res. Number Theory 4 (2018), Art. 5, 30 pp.Google Scholar
Benedetto, R., Briend, J.-Y. and Perdry, H.. Dynamique des polynômes quadratiques sur les corps locaux. J. Théor. Nombres Bordeaux 19 (2007), 325–336.CrossRefGoogle Scholar
Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. of Math. (2) 133 (1991), 73–169.CrossRefGoogle Scholar
Devaney, R.. An Introduction to Chaotic Dynamical Systems, 2nd edn. Addison-Wesley, Redwood City, CA, 1989.Google Scholar
Devaney, R. and Nitecki, Z.. Shift automorphisms in the Hénon mapping. Comm. Math. Phys. 67 (1979), 137–146.CrossRefGoogle Scholar
Folland, G. B.. Real Analysis: Modern Techniques and Their Applications (Pure and Applied Mathematics) , 2nd edn. John Wiley, New York, 1999.Google Scholar
Hénon, M.. A two-dimensional mapping with a strange attractor. Comm. Math. Phys. 50 (1976), 69–77.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.CrossRefGoogle Scholar
Woodcock, C. F. and Smart, N. P.. p-adic chaos and random number generation. Exp. Math. 7 (1998), 333–342.CrossRefGoogle Scholar
Young, L.-S.. What are SRB measures, and which dynamical systems have them? J. Stat. Phys. 108 (2002), 733–754.CrossRefGoogle Scholar