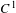Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T14:47:39.141Z Has data issue: false hasContentIssue false
  • English
  • Français

$C^{1}$-openness of non-uniform hyperbolic diffeomorphisms with bounded 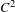$C^{2}$-norm

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  06 June 2019

CHAO LIANG ,
KARINA MARIN  and
JIAGANG YANG
CHAO LIANG
Affiliation:
School of Statistics and Mathematics, Central University of Finance and Economics, Beijing100081, China email chaol@cufe.edu.cn
KARINA MARIN
Affiliation:
Departamento de Matemática, Instituto de Ciências Exatas (ICEx), Universidade Federal de Minas Gerais, Brazil email kmarin@mat.ufmg.br
JIAGANG YANG
Affiliation:
Departamento de Geometria, Instituto de Matemática e Estatística, Universidade Federal Fluminense, Niterói, Brazil email yangjg@impa.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the 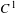$C^{1}$-topological properties of the subset of non-uniform hyperbolic diffeomorphisms in a certain class of 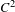$C^{2}$ partially hyperbolic symplectic systems which have bounded 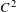$C^{2}$ distance to the identity. In this set, we prove the stability of non-uniform hyperbolicity as a function of the diffeomorphism and the measure, and the existence of an open and dense subset of continuity points for the center Lyapunov exponents. These results are generalized to the volume-preserving context.

Keywords

non-uniform hyperbolicitypartial hyperbolic diffeomorphismsLyapunov exponents

MSC classification

Primary: 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Secondary: 37D30: Partially hyperbolic systems and dominated splittings
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 11 , November 2020 , pp. 3078 - 3104
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Santamaria, J. and Viana, M.. Holonomy invariance: rough regularity and applications to Lyapunov exponents. Astérisque 358 (2013), 13–74.Google Scholar
Avila, A. and Viana, M.. Extremal Lyapunov exponents: an invariance principle and applications. Invent. Math. 181 (2010), 115–178.CrossRefGoogle Scholar
Avila, A. and Viana, M.. Stable accessibility with 2-dimensional center. Preprint, http://www.impa.br/∼viana/.Google Scholar
Backes, L., Brown, A. and Butler, C.. Continuity of Lyapunov exponents for cocycles with invariant holonomies. J. Mod. Dyn. 12 (2018), 223–260.CrossRefGoogle Scholar
Barreira, L., Pesin, Y. and Schmeling, J.. Dimension and product structure of hyperbolic measures. Ann. of Math. (2) 149 (1999), 755–783.CrossRefGoogle Scholar
Bochi, J.. Genericity of zero Lyapunov exponents. Ergod. Th. & Dynam. Sys. 22 (2002), 1667–1696.CrossRefGoogle Scholar
Bochi, J.. C 1 generic symplectic diffeomorphism: partial hyperbolicity and zero center Lyapunov exponents. J. Inst. Math. Jussieu 9(1) (2010), 49–93.CrossRefGoogle Scholar
Bochi, J., Bonatti, C. and Díaz, L. J.. Robust criterion for the existence of nonhyperbolic ergodic measures. Comm. Math. Phys. 344(3) (2016), 751–795.CrossRefGoogle Scholar
Bochi, J. and Viana, M.. The Lyapunov exponents of generic volume preserving and symplectic systems. Ann. of Math. (2) 161(3) (2005), 1423–1485.CrossRefGoogle Scholar
Bocker-Neto, C. and Viana, M.. Continuity of Lyapunov exponents for random two-dimensional matrices. Ergod. Th. & Dynam. Sys. 37 (2017), 1413–1442.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity (Encyclopedia of Mathematical Sciences, Vol. 102) . Springer, Berlin, 2005.Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171(1) (2010), 451–489.CrossRefGoogle Scholar
Furstenberg, H. and Kesten, H.. Products of random matrices. Ann. Math. Statist. 31 (1960), 457–469.CrossRefGoogle Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, Berlin, 1977.CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 131–173.CrossRefGoogle Scholar
Ledrappier, F.. Positivity of the exponent for stationary sequences of matrices. Lyapunov Exponents (Bremen, 1984) (Lecture Notes in Mathematics, 1186) . Springer, Berlin, 1986, pp. 56–73.CrossRefGoogle Scholar
Ledrappier, F. and Strelcyn, J. M.. A proof of the estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2 (1982), 203–219.CrossRefGoogle Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms I. Characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122(3) (1985), 509–539.CrossRefGoogle Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms II. Relations between entropy, exponents and dimension. Dimension and product structure of hyperbolic measures. Ann. of Math. (2) 122(3) (1985), 540–574.CrossRefGoogle Scholar
Liang, C., Marin, K. and Yang, J.. Lyapunov exponents of partially hyperbolic volume-preserving maps with 2-dimensional center bundle. Ann. Inst. H. Poincaré Anal. Non Linéaire 35(6) (2018), 1687–1706.CrossRefGoogle Scholar
Mañé, R.. The Lyapunov exponents of generic area preserving diffeomorphism. International Conference on Dynamical Systems (Montevideo 1995). Longman, Harlow, 1996, pp. 110–119.Google Scholar
Marin, K.. C r -density of (non-uniform) hyperbolicity in partially hyperbolic symplectic diffeomorphisms. Comment. Math. Helv. 91(2) (2016), 357–396.CrossRefGoogle Scholar
Obata, D. and Poletti, M.. On the genericity of positive exponents of conservative skew products with two-dimensional fibers. Preprint, 2018, arXiv:1809.03874.Google Scholar
Pesin, Ya.. Characteristic Lyapunov exponents and smooth ergodic theory. Uspekhi. Mat. Nauk 32(4(196)) (1977), 55–112, 287.Google Scholar
Poletti, M.. Stably positive Lyapunov exponents for symplectic linear cocycles over partially hyperbolic diffeomorphisms. Discrte Contin. Dyn. A 38(10) (2018), 5163–5188.CrossRefGoogle Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Hölder foliations, revisited. J. Mod. Dyn. 6 (2012), 835–908.Google Scholar
Rokhlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Transl. 10 (1952), 1–52. Transl. from Math. Sbornik 25 (1949), 107–150.Google Scholar
Rokhlin, V. A.. Lectures on the entropy theory of measure-preserving transformations. Russ. Math. Surveys 22(5) (1967), 1–52.CrossRefGoogle Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer, New York, 1987.CrossRefGoogle Scholar
Shub, M. and Wilkinson, A.. Stably ergodic approximation: two examples. Ergod. Th. & Dynam. Sys. 20(3) (2000), 875–893.CrossRefGoogle Scholar
Tahzibi, A. and Yang, J.. Invariance Principle and rigidity of high entropy measures. Trans. Amer. Math. Soc. 371 (2019), 1231–1251.CrossRefGoogle Scholar
Viana, M.. Lectures on Lyapunov Exponents. Cambridge University Press, Cambridge, 2014.CrossRefGoogle Scholar
Viana, M. and Yang, J.. Continuity of Lyapunov exponents in the C 0 topology. Israel J. Math. 229(1) (2019), 461–485.CrossRefGoogle Scholar
Wilkinson, A.. Stable ergodicity of the time-one map of a geodesic flow. Ergod. Th. & Dynam. Sys. 18(6) (1998), 1545–1588.CrossRefGoogle Scholar
Xia, Z. and Zhang, H.. A C r closing lemma for a class of symplectic diffeomorphisms. Nonlinearity 19 (2006), 511–516.CrossRefGoogle Scholar
Yang, J.. Entropy along expanding foliations. Preprint, 2016, arXiv:1601.05504.Google Scholar