No CrossRef data available.
Article contents
Cancellations of periodic orbits for non-singular Morse–Smale flows
Published online by Cambridge University Press: 25 May 2023
Abstract
In this work, we explore the dynamical implications of a spectral sequence analysis of a filtered chain complex associated to a non-singular Morse–Smale (NMS) flow 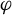 $\varphi $ on a closed orientable
$\varphi $ on a closed orientable 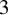 $3$-manifold
$3$-manifold 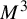 $M^3$ with no heteroclinic trajectories connecting saddle periodic orbits. We introduce the novel concepts of cancellations and reductions of pairs of periodic orbits based on Franks’ morsification and Smale’s cancellation theorems. The main goal is to establish an algebraic-dynamical correspondence between the unfolding of this spectral sequence associated to
$M^3$ with no heteroclinic trajectories connecting saddle periodic orbits. We introduce the novel concepts of cancellations and reductions of pairs of periodic orbits based on Franks’ morsification and Smale’s cancellation theorems. The main goal is to establish an algebraic-dynamical correspondence between the unfolding of this spectral sequence associated to 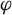 $\varphi $ and a family of flows obtained by cancelling and reducing pairs of periodic orbits of
$\varphi $ and a family of flows obtained by cancelling and reducing pairs of periodic orbits of 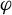 $\varphi $ on
$\varphi $ on 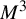 $M^3$. This correspondence is achieved through a spectral sequence sweeping algorithm (SSSA), which determines the order in which these cancellations and reductions of periodic orbits occur, producing a family of NMS flows that reaches a core flow when the spectral sequence converges.
$M^3$. This correspondence is achieved through a spectral sequence sweeping algorithm (SSSA), which determines the order in which these cancellations and reductions of periodic orbits occur, producing a family of NMS flows that reaches a core flow when the spectral sequence converges.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press


