A characterization of Thurston’s Master Teapot

Abstract

We prove an explicit characterization of the points in Thurston’s Master Teapot, which can be implemented algorithmically to test whether a point in $\mathbb {C}\times \mathbb {R}$ belongs to the complement of the Master Teapot. As an application, we show that the intersection of the Master Teapot with the unit cylinder is not symmetrical under reflection through the plane that is the product of the imaginary axis of $\mathbb {C}$ and $\mathbb {R}$.

1 Introduction

The growth rate of a continuous dynamical system $f:X \to X$ , where X is a compact topological space, is the exponential of the topological entropy of f, $e^{h_{\mathrm {top}}(f)}$ . When such a dynamical system admits a Markov partition—as is the case for continuous, multimodal, postcritically finite, self-maps of intervals, or pseudo-Anosov surface diffeomorphisms—a consequence of the Perron–Frobenius theorem is that the growth rate must be a weak Perron number, that is, a real, positive algebraic integer that is not less than the absolute value of any of its Galois conjugates. In [Thu14], Thurston proved that every weak Perron number arises as the growth rate of some continuous, multimodal, postcritically finite, self-maps of intervals. (The analogous question for pseudo-Anosov surface diffeomorphisms remains open.) By considering the set of all interval maps of any modality and any postcritical orbit portrait, Thurston stabilized the question; the question of characterizing the set of growth rates of all postcritically finite interval maps of any fixed modality $d \geq 2$ is more subtle, and remains open. This work investigates growth rates of the family of all continuous, unimodal, critically periodic interval self-maps, which we denote $\mathcal {F}^{cp}_2$ .

Since the growth rates of maps in $\mathcal {F}^{cp}_2$ are known to satisfy a condition involving their Galois conjugates (namely, they are weak Perron numbers), it is natural to consider, for any $f \in \mathcal {F}^{cp}_2$ , the set $\{z \in \mathbb {C} : z \textrm { is a Galois conjugate of the growth rate, } e^{h_{\mathrm {top}}(f)} \textrm {, of } f\}$ . Another, related reason to consider the set of Galois conjugates of $e^{h_{\mathrm {top}}(f)}$ is that the Galois conjugates can be used to construct a ‘lift’ of this real, one-dimensional dynamical system defined by f to a dynamical system defined on $\mathbb {C}^s\times \mathbb {R}^d$ , where r is the number of real Galois conjugates of $e^{h_{\mathrm {top}}(f)}$ and s is the number of non-real complex-conjugate pairs of Galois conjugates (see, e.g., Theorem 2.1 of [Thu14]). The Master Teapot for the family $\mathcal {F}^{cp}_2$ is the set

$$ \begin{align*} {\Upsilon_2^{cp}} := \overline{ \{ (z,\unicode{x3bb}) \in \mathbb{C} \times \mathbb{R} \mid \unicode{x3bb} = e^{h_{\mathrm{top}}(f)} \textrm{ for some } f \in \mathcal{F}^{cp}_2,z \textrm{ is a Galois conjugate of } \unicode{x3bb} \}}. \end{align*} $$

Thurston coined the term ‘Master Teapot’ because plots of finite approximations of this set resemble a teapot, with a roughly cylindrical body over the unit circle, a ‘spout’ consisting of points of the form $\{\unicode{x3bb} ,\unicode{x3bb} \}$ , and a ‘handle’ protruding from the body opposite the spout. (See Figure 1.) Clearly, the geometry and topology of this set encode information about which growth rates are realized by maps in the family $\mathcal {F}^{cp}_2$ . While the geometry of the Master Teapot retains information about which growth rate $\unicode{x3bb} $ corresponds to which Galois conjugate z, it is also interesting to consider the subset of $\mathbb {C}$ formed by plotting all the Galois conjugates (including the growth rate $\unicode{x3bb} $ ) of all maps in $\mathcal {F}^{cp}_2$ in the same copy of $\mathbb {C}$ , and taking the closure. The Thurston set is the set

$$ \begin{align*}{\Omega_2^{cp}} := \overline{ \{z \in \mathbb{C} \mid z \textrm{ is a Galois conjugate of } e^{h_{\mathrm{top}}(f)} \textrm{ for some } f \in \mathcal{F}_2^{cp}\} }.\end{align*} $$

Equivalently, the Thurston set is the projection of the Master Teapot to the complex plane.

Figure 1 A plot of a finite approximation of ${\Upsilon _2^{cp}}$ , showing all points coming from maps in $\mathcal {F}^{cp}$ whose critical orbits have periods at most 23. The two black circles are $S^1\times \{1\}$ and $S^1\times \{2\}$ , where $S^1$ is the unit circle. The color gradients show the height of the plotted points. This figure is from [BDLW19].

The Master Teapot and Thurston set have rich and mysterious geometrical and topological structures that have been investigated in several recent works, including [BDLW19, CKW17, Tho17, Thu14, Tio15, Tio18]. Describing the ‘shape’ of the Master Teapot $\Upsilon _2^{cp}$ or the Thurston set $\Omega _2^{cp}$ is a step toward refining Thurston’s result by characterizing which weak Perron numbers arise as the growth rates of which PCF interval maps. In particular, the ability to prove that a specific point z is not in the Master Teapot—which the algorithms we present in §8 accomplish—provides a necessary condition for a growth rate to be realized by a map in $\mathcal {F}_2^{cp}$ .

In [BDLW19], the authors prove that the Master Teapot $\Upsilon _2^{cp}$ is connected and contains the unit cylinder $S^1 \times [1,2]$ . Furthermore, the intersection of the height- $\unicode{x3bb} $ slice of the Master Teapot,

$$ \begin{align*}\Xi_{\unicode{x3bb}} := \{z \in \mathbb{C} : (z,\unicode{x3bb}) \in \Upsilon_2^{cp}\}\end{align*} $$

with the closed unit disk $\overline {\mathbb {D}}$ grows monotonically with $\unicode{x3bb} $ [BDLW19]. Consequently, the part of the top level slice of the Master Teapot that is inside the unit cylinder, $\Xi _2 \cap \overline {\mathbb {D}}$ , coincides with $\Omega _2^{cp} \cap \overline {\mathbb {D}}$ , the part of the Thurston set inside the unit disk.

The growth rates of PCF self-maps of real intervals may be seen as a specific case of core entropy for PCF complex polynomials. Indeed, the filled Julia set of a PCF complex polynomial contains a forward invariant, finite topological tree, called the Hubbard tree, that contains the critical points of the polynomial; the core entropy of such a polynomial is the topological entropy of the restriction of the dynamics to the Hubbard tree. For a polynomial with real coefficients, the Hubbard tree is a real interval, and so the restriction of the map to the Hubbard tree is a PCF multimodal self-map of an interval. Although we confine our investigation here to self-maps of real polynomials, similar questions could be explored in the complex setting. The interested reader may read more about core entropy for complex polynomials in [GT21, Tio16].

Another motivation for investigating PCF multimodal self-maps of real intervals is that these maps may also be seen as one-dimensional analogs of pseudo-Anosov surface diffeomorphisms. A uniform expander is a continuous, piecewise affine-linear (with finitely many pieces) self-map of an interval such that the derivative on each piece is $\pm \unicode{x3bb} $ for some expansion factor $\unicode{x3bb}> 1$ . Classical results in entropy theory imply that the growth rate of a uniform expander with expansion factor $\unicode{x3bb} $ is $\unicode{x3bb} $ . Milnor and Thurston proved that every continuous, self-map of an interval with finitely many critical points and positive topological entropy is semi-conjugate to a uniform expander with the same topological entropy [MT88]. Both PCF uniform expanders and pseudo-Anosov surface diffeomorphisms are uniformly expanding maps except at finitely many points, admit Markov partitions, and their expansion factors (called the dilatation of a pseudo-Anosov surface diffeomorphism) coincide with their growth rates. Constructions of pseudo-Anosov surface diffeomorphisms from uniform expanders are explored in [BRW16, Far21]. Characterizing the set of dilatations realized by pseudo-Anosov surface diffeomorphisms remains an open question.

The Master Teapot and Thurston set are also closely related to the theory of $\beta $ - and generalized $\beta $ -expansions (cf. [DMP11, Ǵ7, IS09, LSS16, Ste13]), roots of Littlewood, Newman, and Borwein polynomials (cf. [BEL08, HM14, Kon99, Muk10, OP93, SS06]), and dynamics of iterated function systems (cf. [Ban02, BH85, Sol04, SX03]).

1.1 Overview of main results

The main contribution of this paper is an explicit characterization of the Master Teapot ${\Upsilon _2^{cp}}$ —necessary and sufficient conditions for a point to be in ${\Upsilon _2^{cp}}$ . (The part of the Master Teapot inside the unit cylinder $\mathbb {D} \times [1,2]$ is described by Theorem 1.7 and the part outside the unit cylinder by Theorem 1.8.) Theorem 1.7 establishes a new connection between horizontal slices of the Master Teapot and iterated function systems. Specifically, the part in $\mathbb {D}$ of each horizontal slice of the Teapot can be viewed as an analog of the Mandelbrot set for a family of ‘restricted iterated function systems’ (cf. Remark 1.15). From this characterization, we prove an algorithm (§8) for showing that certain weak Perron numbers cannot be the exponent of the topological entropy of a critically periodic unimodal interval map. As an application of this algorithm, we prove that the part of the Master Teapot inside the unit cylinder is not symmetrical with respect to reflection across the imaginary axis (Theorem 1.14). Conjecture 1.16 proposes that an analogy of the Mandelbrot–Julia set correspondence holds for horizontal slices and limit sets of restricted iterated function systems.

1.2 Precise statement of results and commentary

To state the results precisely, we introduce some terminology and notation.

First, we define words and sequences in the alphabet $\{0, 1\}$ .

Definition 1.1

1. (1) A sequence $w=w_1w_2\ldots $ is an element in $\{0, 1\}^{\mathbb {N}}$ . The shift map $\sigma : \{0,1\}^{\mathbb {N}} \to \{0,1\}^{\mathbb {N}}$ is defined by removing the first element of a sequence, that is, $\sigma (w_1w_2w_3\ldots ) :=w_2w_3\ldots .$

2. (2) A word $w=w_1w_2\ldots w_n$ is an element in $\{0, 1\}^n$ for some positive integer n. The number n is called the length of the word w and is denoted by $|w|$ .

3. (3) For $n \in \mathbb {N}$ , the reverse function ${\textrm {Rev}} : \{0,1\}^n \to \{0,1\}^n$ is defined as

   $$ \begin{align*} {\textrm{Rev}}(w_1w_2\ldots w_n):=w_nw_{n-1}\ldots w_1.\end{align*} $$

4. (4) For $k \in \mathbb {N}$ , the k-prefix of a sequence $w=w_1w_2\ldots $ is the word

   $$ \begin{align*}{\textrm{Pre}}_k(w):=w_1\ldots w_k.\end{align*} $$

5. (5) For a word $w=w_1 \ldots w_n$ of length n and a natural number $k \leq n$ , the k-prefix and k-suffix of w are the words

   $$ \begin{align*} {\textrm{Pre}}_k(w) & :=w_1\ldots w_k,\\ {\textrm{Suf}}_k(w) &:=w_{n-k+1}w_{n-k+2}\ldots w_n. \end{align*} $$

Next, we relate words and sequences with dynamics on $\mathbb {C}$ via the following definitions.

Definition 1.2

1. (1) For any $z\in \mathbb {C}$ , define maps $f_{0,z},f_{1,z}: \mathbb {C} \to \mathbb {C}$ by

   $$ \begin{align*}f_{0, z}(x):=zx, \quad f_{1, z}(x):=2-zx.\end{align*} $$

2. (2) For any $w=w_1\ldots w_n$ and $z \in \mathbb {C}$ , set

   $$ \begin{align*}F(w,z):=f_{w_n,z}\circ \cdots \circ f_{w_1,z}(1).\end{align*} $$

3. (3) For any sequence $w=w_1w_2\ldots $ and any $z \in \mathbb {C}$ with $|z|>1$ , set

   $$ \begin{align*} H(w, z) := & \lim_{n\rightarrow\infty}(-1)^{(\sum_{i=1}^nw_i)}z^{-n} F({\textrm{Pre}}_n(w), z) \\ = &\lim_{n\rightarrow\infty}(-1)^{(\sum_{i=1}^nw_i)}z^{-n}f_{w_n,z}\circ\cdots \circ f_{w_1, z}(1). \end{align*} $$

4. (4) For any sequence $w=w_1w_2\ldots $ and $z \in \mathbb {C}$ with $|z|<1$ , set

   $$ \begin{align*} G(w, z):= & \lim_{n\rightarrow\infty}F({\textrm{Rev}}({\textrm{Pre}}_n(w)), z) \\ = &\lim_{n\rightarrow\infty}f_{w_1,z}\circ \cdots \circ f_{w_n, z}(1). \end{align*} $$

The following definition is partly from [MT88].

Definition 1.3

1. (1) The cumulative sign of a word $w=w_1w_2\ldots w_n$ is defined as $s(w):=(-1)^{\sum _iw_i}$ .

2. (2) The twisted lexicographic order $\le _E$ is a total ordering on the set of sequences, defined as follows: $w<_Ew'$ if and only if there is some $k\in \mathbb {N}$ such that ${\textrm {Pre}}_{k-1}(w){\kern-1pt}={\kern-1pt}{\textrm {Pre}}_{k-1}(w')$ , and $s({\textrm {Pre}}_{k-1}(w))(w^{\prime }_{k}{\kern-1pt}-{\kern-1pt}w_{k})>{\kern-1pt}0$ . In other words, $w {\kern-1pt}<_E w'$ if and only if, denoting by k the index of the first letter where w and $w'$ differ, either $w^{\prime }_k>w_k$ and the common $(k-1)$ -prefix has positive cumulative sign, or $w^{\prime }_k<w_k$ and the common $(k-1)$ -prefix has negative cumulative sign.

3. (3) We define the total order $\le _E$ on the set of words of length n exactly the same way as above.

Definition 1.4

1. (1) Let $\unicode{x3bb} \in (1, 2]$ . We call the map $f_{\unicode{x3bb} }:[0,1] \to [0,1]$ given by

   $$ \begin{align*}f_\unicode{x3bb}(x)=\begin{cases} \unicode{x3bb} x, & x\leq 1/\unicode{x3bb}, \\ 2-\unicode{x3bb} x, & x>1/\unicode{x3bb},\end{cases}\end{align*} $$
   the $\unicode{x3bb} $ -tent map. Let $I_{0, \unicode{x3bb} }=[0, 1/\unicode{x3bb} ]$ , $I_{1, \unicode{x3bb} }=[1/\unicode{x3bb} , 1]$ .

2. (2) The $\unicode{x3bb} $ -itinerary, denoted as $\mathrm {{It}}_\unicode{x3bb} $ , is the minimum (with respect to $\leq _E$ ) sequence w such that for any $k\geq 0$ , $f_\unicode{x3bb} ^k(1)\in I_{w_{k+1},\unicode{x3bb} }$ .

One can easily check that $\mathrm {{It}}_{\unicode{x3bb} }$ is the itinerary of $1$ under $f_\unicode{x3bb} $ in the convention of the Milnor–Thurston kneading theory.

Now we introduce a combinatorial condition on sequences.

Definition 1.5. For $\unicode{x3bb} \in (1,2]$ , a sequence w is called $\unicode{x3bb} $ -suitable if for every $\unicode{x3bb} '\in (\unicode{x3bb} , 2]$ , the following conditions hold:

1. (1) ${\textrm {Rev}} ( {\textrm {Pre}}_n(w)) \leq _E {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$ for all $n \in \mathbb {N}$ ;

2. (2) if ${\textrm {Rev}}({\textrm {Pre}}_n(w)) = {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$ , then the cumulative sign $s({\textrm {Pre}}_n(w)) = -1$ ;

3. (3) if $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots , k \in \mathbb {N}$ , then w does not contain $k+1$ consecutive $0$ s (that is, if $\mathrm {{It}}_{\unicode{x3bb} '}$ starts with $1$ followed by $k\ 0$ s and then $1$ , writing w as $w=w_1w_2\ldots ,$ there does not exist $n \in \mathbb {N}$ such that $w_i = 0$ for all $n \leq i \leq n+k$ );

4. (4) if $k \in \mathbb {N}$ satisfies $\sqrt {2}\leq \unicode{x3bb} ^{2^k}<2$ , then $w=\mathfrak {D'}^k(w')$ for some sequence $w'$ , where $\mathfrak {D'}$ is the map that replaces $0$ with $11$ and $1$ with $01$ , such that for every $\unicode{x3bb} '>\unicode{x3bb} ^{2^k}$ , if $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots ,$ then $w'$ does not contain $k+1$ consecutive $0$ s.

Remark 1.6. Every sequence is (vacuously) $2$ -suitable.

For $\unicode{x3bb} \in (1, 2)$ , let ${\Xi }_\unicode{x3bb} $ be a height- $\unicode{x3bb} $ slice of the Master Teapot $\Upsilon _2$ :

$$ \begin{align*}{\Xi}_\unicode{x3bb}:=\{z: (z, \unicode{x3bb})\in \Upsilon_2\}.\end{align*} $$

We will use the following notation:

$$ \begin{align*} \mathbb{D} & := \{z \in \mathbb{C} : |z| <1\}\quad \textrm{the open unit disk}, \\ \overline{\mathbb{D}} & := \{z \in \mathbb{C} : |z| \leq 1\}\quad \textrm{the closed unit disk},\\ S^1 & := \{z \in \mathbb{C} : |z| = 1\}\quad \textrm{the unit circle} ,\\ \mathcal{C} & := \overline{\mathbb{D}} \times [1,2]\quad \textrm{the closed `unit cylinder'}. \end{align*} $$

Our main theorem is the following.

Theorem 1.7. For any $\unicode{x3bb} \in (1,2]$ , the part of the slice ${\Xi }_\unicode{x3bb} $ inside the closed unit disk can be characterized as

$$ \begin{align*}{\Xi}_\unicode{x3bb} \cap \overline{\mathbb{D}} = S^1\cup \{z\in\mathbb{D}: G(w, z)=1\text{ for some }\unicode{x3bb}\text{-suitable sequence }w \}.\end{align*} $$

There is a similar characterization for outside the unit disc, which follows directly from results in [Tio18].

Theorem 1.8. For any $\unicode{x3bb} \in (1,2)$ , the part of the slice ${\Xi }_\unicode{x3bb} $ outside the unit disk can be characterized as follows.

• • If the $\unicode{x3bb} $ -tent map is not critically periodic, then

  $$ \begin{align*}{\Xi}_\unicode{x3bb} \setminus \overline{\mathbb{D}}= \{z \in \mathbb{C} \setminus \overline{\mathbb{D}}: H(\mathrm{{It}}_\unicode{x3bb}, z)=0 \}.\end{align*} $$

• • If the $\unicode{x3bb} $ -tent map is critically periodic with period p, then

  $$ \begin{align*}{\Xi}_\unicode{x3bb} \setminus \overline{\mathbb{D}}= \{z \in \mathbb{C} \setminus \overline{\mathbb{D}}: H(\mathrm{{It}}_\unicode{x3bb}, z)=0\text{ or }z^p=2 \}.\end{align*} $$

Remark 1.9. Theorems 1.7 and 1.8 both provide algorithms to certify that a point is in the complement of ${\Xi }_\unicode{x3bb} $ . This is useful since the definition of ${\Upsilon _2^{cp}}$ is not constructive, as it involves taking a closure. Section 8 describes these algorithms. Figure 4 is a finite approximation of ${\Xi }_{1.8} \cap \overline {\mathbb {D}}$ using Theorem 1.7, and Figure 2 is a finite approximation of ${\Upsilon _2^{cp}}\backslash (\overline {\mathbb {D}}\times [1, 2])$ using Theorem 1.8.

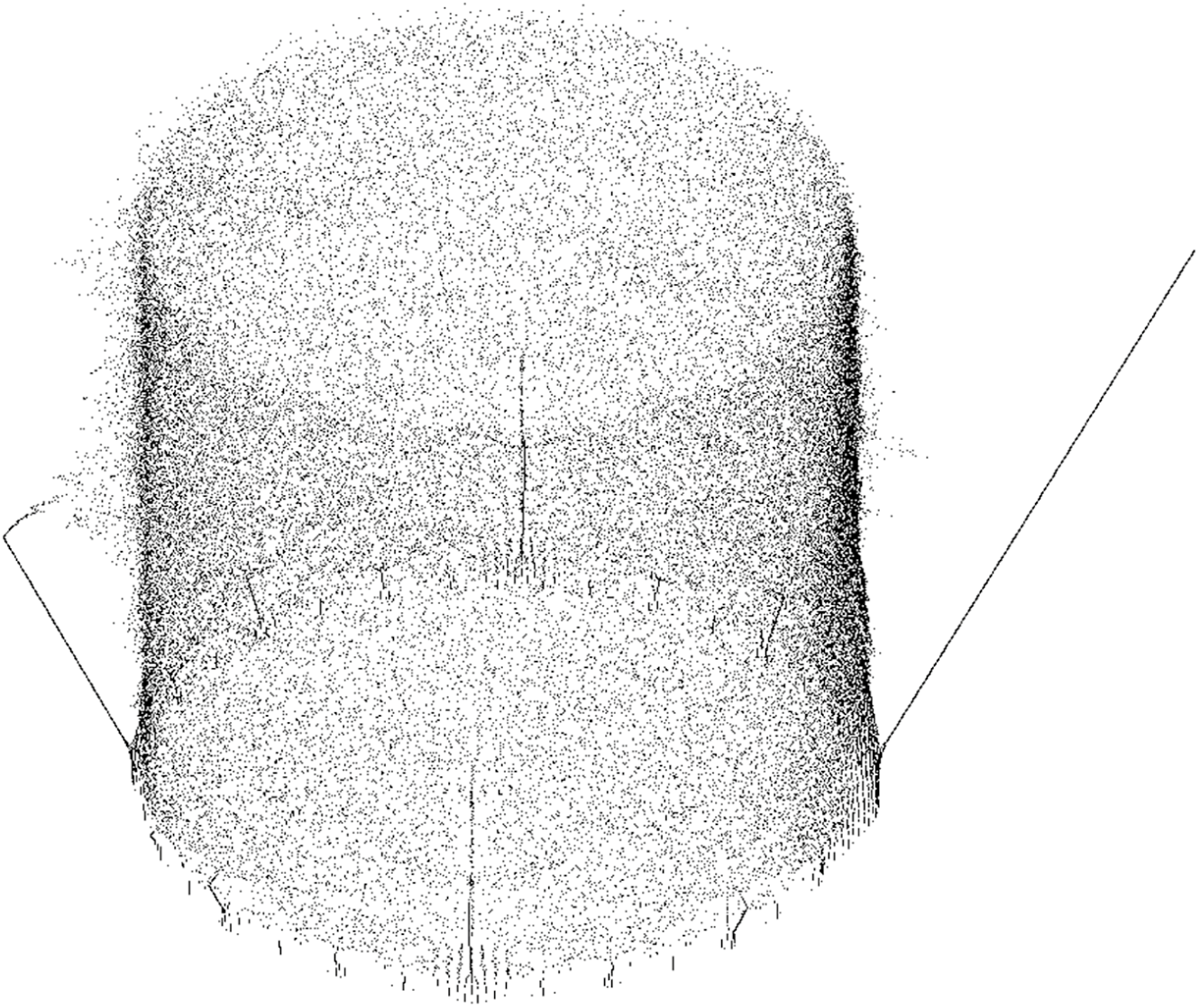
Figure 2 A constructive approximation of the part of ${\Upsilon _2^{cp}}$ outside the unit cylinder. This plot shows the 56 737 points outside the cylinder $S^1 \times [1,2]$ that are roots of the degree 100 partial sums of the kneading power series for $1000$ different growth rates $\unicode{x3bb} $ in $[1,2]$ . The ‘spout’ on the right side of the image consists of points of the form $(\unicode{x3bb} ,\unicode{x3bb} )$ .

Remark 1.10. Since the set of $\unicode{x3bb} $ -suitable sequences is semicontinuous with $\unicode{x3bb} $ (Lemma 5.5), Theorem 1.7 implies that if $1<\unicode{x3bb} <\unicode{x3bb} ' \leq 2$ , then

$$ \begin{align*}{\Xi}_\unicode{x3bb}\cap\overline{\mathbb{D}}\subseteq {\Xi}_{\unicode{x3bb}'}\cap\overline{\mathbb{D}},\end{align*} $$

which is the ‘persistence theorem’ proved in [BDLW19]. However, our proof of Theorem 1.7 depends on the persistence theorem in [BDLW19].

Remark 1.11. Tiozzo showed in [Tio18] that

$$ \begin{align*}\Omega_2^{cp} \cap \overline{\mathbb{D}} = S^1 \cup \{z \in \mathbb{D} : G(w,z) = 1 \textrm{ for some sequence } w\},\end{align*} $$

and the persistence theorem [BDLW19] shows that $\Omega _2 \cap \overline {\mathbb {D}} = {\Xi }_2 \cap \overline {\mathbb {D}}$ . It is also known that the unit cylinder is in the teapot, that is, $S^1 \times [1,2] \subset \Upsilon _2^{cp}$ [BDLW19]. Since every sequence is $2$ -suitable, this proves the conclusion of Theorem 1.7 for the top level of the teapot, the case $\unicode{x3bb} = 2$ .

Remark 1.12. Our first step towards proving Theorem 1.7 is proving Theorem 4.5, an alternative characterization of slices $\Xi _{\unicode{x3bb} } \cap \overline {\mathbb {D}}$ . A corollary of Theorem 4.5 is that all roots in $\overline {\mathbb {D}}$ of all Parry polynomials coming from admissible words—even reducible Parry polynomials—are in the Thurston set $\Omega _2^{cp}$ .

Corollary 1.13. $\Omega _2^{cp} \cap \overline {\mathbb {D}}$ is the closure of the set of all roots in $\overline {\mathbb {D}}$ of all Parry polynomials associated to admissible words.

In particular, when using Parry polynomials to plot approximations of $\Omega _2^{cp}$ , it is not necessary to check whether the Parry polynomials are irreducible.

As an application of Theorem 1.7, we will show the following.

Theorem 1.14. The part of the Master Teapot inside the unit cylinder is not symmetrical with respect to reflection across the imaginary axis, that is, ${\Upsilon _2^{cp}} \cap \mathcal {C}$ is not invariant under the map $(z,\unicode{x3bb} ) \mapsto (-z,\unicode{x3bb} )$ .

Since Galois conjugates occur in complex conjugate pairs, it is immediate that $(x+iy,\unicode{x3bb} ) \in {\Upsilon _2^{cp}}$ if and only if $(x-iy,\unicode{x3bb} ) \in {\Upsilon _2^{cp}}$ .

Theorem 1.14 is surprising because the Thurston set, ${\Omega _2^{cp}}$ , which is the projection to $\mathbb {C}$ of ${\Upsilon _2^{cp}}$ , is symmetrical under the map $z \mapsto -z$ (Proposition 9.1). However, this asymmetry in the Master Teapot is confined to the slices of heights $\geq \sqrt {2}$ ; one can prove, via the renormalization procedure described in §2.3, that the unit cylinder part of slices of height $< \sqrt {2}$ is symmetrical under reflection across the imaginary axis.

Remark 1.15. Theorem 1.7 allow us to interpret each slice ${\Xi }_\unicode{x3bb} \cap \mathbb {D}$ as an analogy of the Mandelbrot set. The conclusion of Theorem 1.7 for the top slice (cf. Remark 1.11) allows one to characterize ${\Xi }_2$ as the union of $S_1$ and the set of all parameters $z \in \mathbb {D}$ such that the point $1$ is an element of the limit set $\Lambda _z$ associated to the iterated function system generated by $f_{0,z}$ and $f_{1,z}$ . Theorem 1.7 suggests viewing ${\Xi }_\unicode{x3bb} \cap \mathbb {D}$ as the set of parameters z for which the point $1$ is an element of the ‘limit set’ associated to the ‘restricted iterated function system’ generated by $f_{0,z}$ and $f_{1,z}$ in which only the compositions represented by $\unicode{x3bb} $ -suitable sequences are allowed.

Based on numerical experiments, we propose the following conjectured analogy of the Julia–Mandelbrot correspondence [DH85, Lei90].

Conjecture 1.16. For any complex number $|z|<1$ , any $\unicode{x3bb} \kern1.2pt{\in}\kern1.2pt (1, 2]$ , the set ${\{z'-z: z'\in {\Xi }_\unicode{x3bb} \}}$ is asymptotically similar to the set

$$ \begin{align*}J_z=\{G(w, z)-1:w\text{ is }\unicode{x3bb}\text{-suitable}\}.\end{align*} $$

By these two sets being asymptotically similar, we mean there exists a real number $r>0$ and sequences $(t_n), (t^{\prime }_n) \in \mathbb {C}$ with $t_n, t_n' \to \infty $ such that, denoting Hausdorff distance by $d_{\textrm {Haus}}$ ,

$$ \begin{align*}\lim_{n \to \infty} d_{\textrm{Haus}} ( \overline{B_r(0)} \cap (t_n({\Xi}_\unicode{x3bb}-z)), \overline{B_r(0)} \cap (t_n' J_z) ) = 0.\end{align*} $$

If Conjecture 1.16 is true, or at least true for ‘enough’ points z, we would also be able to show the following.

Conjecture 1.17. There exists $\unicode{x3bb} \in (1, 2)$ such that ${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$ has infinitely many connected components.

Figure 3 shows a constructive plot (in black) of the slice ${\Xi }_{1.8} \cap \overline {\mathbb {D}}$ , while Figure 4 shows (in white) points of $\overline {\mathbb {D}} \setminus {\Xi }_{1.8}$ . Comparison of these images suggests the existence of multiple small connected components in the region $\textrm {Re}(z) < 0$ near the inner boundary of the ‘ring.’

Figure 3 A constructive plot of an approximation of the slice ${\Xi }_{1.8} \cap \mathbb {D}$ . The plotted black points are all the roots of modulus $\leq 1$ of all Parry polynomials for superattracting tent maps with growth rate $<1.8$ and critical length at most $29$ .

Figure 4 The upper half of the slice ${\Upsilon _2^{cp}} \cap (\mathbb {D} \times \{1.8\})$ plotted using Theorem 1.7. Specifically, the plotted white points are shown to be in the complement of ${\Upsilon _2^{cp}}$ (by checking the condition of Theorem 1.7 for all $m \leq 18$ ).

The Thurston set ${\Omega _2^{cp}}$ is known to be path-connected and locally connected [Tio18, Theorem 1.3]. It follows from Theorem 1.8 that for many heights $\unicode{x3bb} \in (1,2]$ , the part of the slice of height $\unicode{x3bb} $ that is outside the unit cylinder consists of more than one connected component.

Conjecture 1.17 could be potentially proven by computation via an effective version of Theorem 1.7 similar to Proposition 8.4. However, a tighter bound than that obtained in Proposition 8.4 would probably be needed for the computation to be feasible.

The structure of the paper is as follows.

Section 2 provides definitions and notation for Parry polynomials, admissible and dominant words and sequences, growth rates, and the renormalization/doubling operators.

Section 3 proves some elementary results about the doubling map which we will need in later sections to extend results about the top part of the teapot to the part with height $<\sqrt {2}$ .

Section 4 proves Theorem 4.5, which implies that all roots in the unit disk of all Parry polynomials associated to admissible words are in the teapot.

Section 5 discusses $\unicode{x3bb} $ -suitability and proves Lemma 5.7, which is the key combinatorial result we need to prove Theorem 1.7.

Section 6 uses Theorem 4.5 and Lemma 5.7 to prove Theorem 1.7.

Section 7 proves Theorem 1.8.

Section 8 presents algorithms, derived from Theorems 1.7 and 1.8, which will detect if a point $(z,\unicode{x3bb} ) \in \mathbb {C} \times \mathbb {R}$ belongs to the complement of the height- $\unicode{x3bb} $ slice ${\Xi }_{\unicode{x3bb} }$ , and proves lemmas that justify the algorithms.

Section 9 proves Theorem 1.14 by exhibiting a point $(z,\unicode{x3bb} )$ that is in the teapot and using the algorithm from §8 to prove that $(-\bar {z},\unicode{x3bb} )$ is in the complement of the slice ${\Xi }_{\unicode{x3bb} }$ .

2 Preliminaries

2.1 Concatenation

We use $\cdot $ or just adjacency to denote concatenations, that is, for any word $w=w_1\ldots w_n$ and any word or sequence $v=v_1v_2\ldots\, $ ,

$$ \begin{align*}w\cdot v = wv = w_1\ldots w_n v_1 v_2 \ldots.\end{align*} $$

We denote the concatenation of n copies of a word w by $w^n$ for $n \in \mathbb {N} \cup \{\infty \}$ .

2.2 Parry polynomials

Let w be a word with positive cumulative sign. The Parry polynomial of w, $P_w:\mathbb {C} \to \mathbb {C}$ , is defined as

$$ \begin{align*}P_w(z):=F(w, z)-1\end{align*} $$

(cf. [BDLW19, Definition 2.7]). It is evident that if $\mathrm {{It}}_\unicode{x3bb} =w^\infty $ , then $\unicode{x3bb} $ is a root of $P_w$ , and hence all Galois conjugates of $\unicode{x3bb} $ must be roots of $P_w$ .

One can check by simple bookkeeping that for any word w of positive cumulative sign, $P_w(z)$ , $G({\textrm {Rev}}(w)^\infty , z)$ and $H(w^\infty , z)$ satisfy the following relationship.

Lemma 2.1. If w is of length n and has positive cumulative sign, then

$$ \begin{align*}P_w(z)=(1-z^n)G(\mathrm{{Rev}}(w)^\infty, z )=z^n(1-z^{-n})H(w^\infty,z).\end{align*} $$

2.3 Admissibility, itineraries, and dominance

The shift map $\sigma $ is defined on sequences by

$$ \begin{align*}\sigma(w_1w_2w_3\ldots) = (w_2w_3\ldots).\end{align*} $$

A sequence $w=w_1w_2\ldots $ is a generalized symbolic coding of $f_\unicode{x3bb} $ for some $\unicode{x3bb} \in (1,2]$ if and only if

$$ \begin{align*}f^k_{\unicode{x3bb}}(1) \in I_{w_{k+1},\unicode{x3bb}}\end{align*} $$

for every integer $k \geq 0$ . Because the point $1/\unicode{x3bb} $ belongs to both intervals $I_{0,\unicode{x3bb} }$ and $I_{1,\unicode{x3bb} }$ , there may exist more than one generalized symbolic coding for the itinerary of the point $1$ under $f_{\unicode{x3bb} }$ . The $\unicode{x3bb} $ -itinerary $\mathrm {{It}}_{\unicode{x3bb} }$ is the least (with respect to $\leq _E$ ) such generalized symbolic coding.

A sequence w starting with $10$ is called admissible if

$$ \begin{align*}\sigma^k(w)\le_E w\end{align*} $$

for all $k \in \mathbb {N}$ . A word w is called admissible if w has positive cumulative sign and $w^\infty $ is admissible.

We will use the following immediate consequence of Theorem 12.1 of [MT88].

Theorem 2.2. For every $\unicode{x3bb} \in (1,2]$ , $\mathrm {{It}}_{\unicode{x3bb} }$ is admissible.

Proposition 2.3. [BDLW19]

Let w be a word with positive cumulative sign. If w is admissible and the associated Parry polynomial, $P_w(z)$ , can be written as the product of $(z-1)$ and another irreducible factor, then $w^{\infty } = \mathrm {{It}}_{\unicode{x3bb} }$ for some $\unicode{x3bb} \in (1,2]$ .

The following is a straightforward corollary [MT88, Theorem 13.1].

Corollary 2.4. If $1 < \unicode{x3bb} < \unicode{x3bb} ' \leq 2$ , then $\mathrm {{It}}_{\unicode{x3bb} }<_E \mathrm {{It}}_{\unicode{x3bb} '}$ .

A word w is called dominant (cf. [BDLW19, Definition 4.1, Lemma 4.2]) if it has positive cumulative sign, and for any $1\leq k\leq |w|-1$ ,

$$ \begin{align*}{\textrm{Suf}}_k(w)\cdot 1<_E{\textrm{Pre}}_{k+1}(w).\end{align*} $$

Every dominant word is admissible, but admissible words may not be dominant. A key property of the dominant words is the following, which is proved in [Tio15] and reviewed in [BDLW19, Proposition 4.4].

Proposition 2.5. If $\unicode{x3bb} \in (\sqrt {2}, 2)$ and $\mathrm {{It}}_\unicode{x3bb} =w^\infty $ , then for any $n>0$ , there exists a word $w'$ such that $w^nw'$ is dominant.

2.4 Growth rates and critically periodic tent maps

When a continuous self-map f of an interval is postcritically finite, the exponential of its topological entropy, $e^{h_{\mathrm {top}}(f)}$ , also called its growth rate, is a weak Perron number—a real positive algebraic integer whose modulus is greater than or equal to that of all of its Galois conjugates. This is because cutting the interval at the critical and postcritical sets yields a Markov partition; each of the resulting subintervals is mapped to a finite union of subintervals. The leading eigenvalue of the associated incidence matrix is $e^{h_{\mathrm {top}}(f)}$ , which the Perron–Frobenius theorem implies is a weak Perron number.

In the present work, we consider growth rates of critically periodic unimodal interval self-maps. A unimodal map f is said to be critically periodic if, denoting the critical point of f by c, there exists $n \in \mathbb {N}$ such that $f^n(c) = c$ . A theorem of Milnor and Thurston [MT88, Theorem 7.4] tells us that, from the point of view of entropy, instead of considering all critically periodic unimodal maps, we only need to consider critically periodic tent maps. For tent maps, it is easy to see that the growth rate is just the slope $\unicode{x3bb} $ .

2.5 Renormalization and doubling

As shown in [BDLW19, §3], for any $1< \unicode{x3bb} <\sqrt {2}$ , the tent map $f_\unicode{x3bb} $ is critically periodic if and only if the tent map $f_{\unicode{x3bb} ^2}$ is critically periodic. (This phenomenon is related to renormalization of the Mandelbrot set.) Furthermore, whenever $1<\unicode{x3bb} <\sqrt {2}$ , $\mathrm {{It}}_{\unicode{x3bb} }$ can be obtained from $\mathrm {{It}}_{\unicode{x3bb} ^2}$ by replacing each $1$ in $\mathrm {{It}}_{\unicode{x3bb} }$ with $10$ and each $0$ in $\mathrm {{It}}_{\unicode{x3bb} }$ with $11$ . That is, the doubling map $\mathfrak {D}:\{0,1\}^n \to \{0,1\}^{2n}$ , $n \in \mathbb {N} \cup \{\infty \}$ , defined by

$$ \begin{align*}\mathfrak{D}(w_1 w_2 \ldots ) = 1 \cdot (1-w_1) \cdot 1 \cdot (1-w_2) \cdot \ldots ,\end{align*} $$

satisfies $\mathfrak {D}(\mathrm {{It}}_{\unicode{x3bb} ^2}) = \mathrm {{It}}_{\unicode{x3bb} }$ whenever $f_{\unicode{x3bb} }$ with $1 < \unicode{x3bb} < 2$ is critically periodic. We say that a sequence w is renormalizable if there exists a sequence $w'$ such that $w=\mathfrak {D}(w')$ ; in this case, we say that w is the doubling of $w'$ and call $w'$ the renormalization of w. We define renormalizable, doubling, and renormalization for words analogously.

Remark 2.6. The ‘renormalization’ we are considering here is only the period- $2$ renormalization, that is, the inverse of tuning by the basilica. The reason is that higher order renormalization would create roots in the $P_w$ that are Galois conjugate of the leading root.

3 Properties of the doubling map

The goal of this section is to prove some elementary properties of renormalizable words and sequences that we will use in later sections to extend the results about the part of the teapot above height $\sqrt {2}$ to the lower part.

Lemma 3.1. The doubling map $\mathfrak {D}$ preserves the twisted lexicographic ordering $\leq _E$ , cumulative signs, and hence also admissibility.

Proof. If the number of $1$ s in a word w equals n, then for any letter a, the number of $1$ s in ${\textrm {Pre}}_{2|w|+1}(\mathfrak {D}(w\cdot a))$ equals $2|w|+1-n$ . It follows that if n is odd, $w\cdot 1 <_E w \cdot 0$ and $\mathfrak {D}(w\cdot 1) <_E \mathfrak {D}(w\cdot 0)$ ; if n is even, $w\cdot 0 <_E w\cdot 1$ and $\mathfrak {D}(w\cdot 0) <_E \mathfrak {D}(w\cdot 1)$ . Thus, $\mathfrak {D}$ preserves $\leq _E$ . Furthermore, if a word w has positive cumulative sign, then the number, n, of $1$ s in w is even, implying that $\mathfrak {D}(w)$ , which contains $2w-n 1$ s, also has positive cumulative sign.

Lemma 3.2. The doubling map $\mathfrak {D}$ takes itineraries to itineraries. That is, if $\unicode{x3bb} ^{2^k} = \unicode{x3bb} '$ , then $\mathfrak {D}^k(\mathrm {{It}}_{\unicode{x3bb} '}) = \mathrm {{It}}_{\unicode{x3bb} }$ .

Proof. By induction, it is easy to see that we only need to prove it for $k=1$ , that is, $\mathfrak {D}(\mathrm {{It}}_{\unicode{x3bb} ^2})=\mathrm {{It}}_\unicode{x3bb} $ . For any $\unicode{x3bb} \leq \sqrt {2}$ , the tent map $f_{\unicode{x3bb} }$ sends the interval $[2/(\unicode{x3bb} +1), 1]$ to $[2-\unicode{x3bb} , 2/(\unicode{x3bb} +1)]$ and vice versa. Hence, $f^2_{\unicode{x3bb} }$ is a tent map from $[2/(\unicode{x3bb} +1), 1]$ of slope $\unicode{x3bb} ^2$ , and any $x=f^{2k}_{\unicode{x3bb} }(1)$ lies on the left-hand side of the critical point of $f^2_{\unicode{x3bb} }$ if and only if x and $f_{\unicode{x3bb} }(x)$ are both to the right of $1/\unicode{x3bb} $ , while $f^{2k}_{\unicode{x3bb} }(1)$ lies on the right-hand side of the critical point of $f^2_{\unicode{x3bb} }$ if and only if x is to the right of $1/\unicode{x3bb} $ and $f_{\unicode{x3bb} }(x)$ is to the left of $1/\unicode{x3bb} $ , and this finishes the proof for the case when $\mathrm {{It}}_{\unicode{x3bb} ^2}$ is not periodic. The case when $\mathrm {{It}}_{\unicode{x3bb} ^2}$ is periodic follows from this argument together with Lemma 3.1.

Proposition 3.3. If w is a word with positive cumulative sign and $w'$ is the renormalization of w, then

$$ \begin{align*}P_w(z)={z-1\over z+1}P_{w'}(z^2).\end{align*} $$

Proof. Suppose w and $w'$ are words satisfying $\mathfrak {D}(w')=w$ . It is easy to see that if $w=w_1w_2\ldots w_{2n}$ has a positive cumulative sign, then $w'=w^{\prime }_1w^{\prime }_2\ldots w^{\prime }_n$ also has a positive cumulative sign. So, the proposition follows from the following more general statement: if $w'$ is any word, w is the doubling of $w'$ , then

(3.1) $$ \begin{align} F(w, z)-1={z-1\over z+1}(F(w', z^2)-1). \end{align} $$

We will prove (3.1) using induction on $|w'|$ . In the base case, $|w'|=1$ , $w'=1$ , or $w'=0$ , and the statement is true by calculation. Now assume the statement is true for all words $w'$ such that $|w'| \leq n-1$ . Let $w'$ and w be words with $|w'| =n$ and $\mathfrak {D}(w')=w$ . Let $w^{\prime }_0$ be $w'$ with the last letter removed, and let $w_0$ be w with the last two letters removed. Then, by the inductive hypothesis,

$$ \begin{align*}F(w_0, z)-1={z-1\over z+1}(F(w^{\prime}_0, z^2)-1).\end{align*} $$

We divide the inductive step into two cases.

Case 1: $w^{\prime }_n=0$ . This implies $w=w_0\cdot 11$ , so

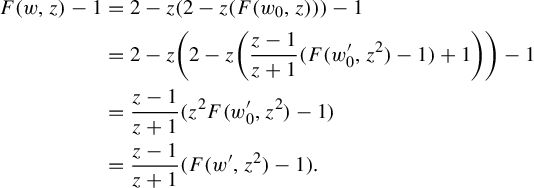$$ \begin{align*} F(w, z)-1 &=2-z (2-z(F(w_0, z)))-1\\ &=2-z \bigg(2-z \bigg({z-1\over z+1}(F(w^{\prime}_0, z^2)-1)+1 \bigg)\bigg)-1\\ &={z-1\over z+1}(z^2F(w^{\prime}_0, z^2)-1)\\ &={z-1\over z+1}(F(w', z^2)-1). \end{align*} $$

Case 2: $w^{\prime }_n=1$ . This implies $w=w_0\cdot 10$ , so

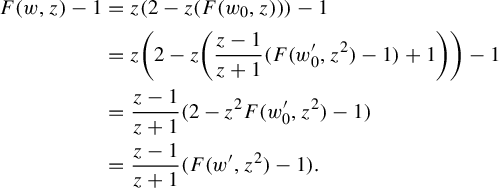$$ \begin{align*} F(w, z)-1 &=z(2-z(F(w_0, z)) )-1\\ &=z \bigg(2-z \bigg({z-1\over z+1}(F(w^{\prime}_0, z^2)-1)+1\bigg)\bigg)-1\\ &={z-1\over z+1} (2-z^2F(w^{\prime}_0, z^2)-1)\\ &={z-1\over z+1}(F(w', z^2)-1).\\[-3.4pc] \end{align*} $$

Proposition 3.4. Let w be an admissible word. Then $w^{\infty }$ renormalizable if only if

$$ \begin{align*}w^\infty<_E \mathrm{{It}}_{\sqrt{2}} \quad (= 10\cdot 1^\infty).\end{align*} $$

Proof. First, it is easy to see that a sequence is renormalizable if and only if all its odd index letters are $1$ , and a word is renormalizable if and only if it has even length and all its odd indexed letters are $1$ . Because any admissible word starts with $10$ , an admissible word w is renormalizable if and only if $w^\infty $ is admissible and renormalizable.

Now suppose $w^\infty $ is admissible and renormalizable. Suppose the second $0$ in $w^\infty $ is at the $k\textrm {th}$ location. It suffices to show that ${\textrm {Pre}}_{k-1}(w^\infty )$ has positive cumulative sign, which is equivalent to showing that k is even, because the $(k-1)$ -prefix of $w^\infty $ and $10\cdot 1^\infty $ are the same. This is an immediate consequence of the admissibility of $w^\infty $ .

Now we prove the other direction. The sequence $w^\infty $ being admissible implies that the first $0$ in $w^\infty $ is at the second location. If we can further prove that the distance between any two consecutive $0$ s is even, then all $0$ s are at even locations, and hence $w^\infty $ is admissible. Denote by $i_k$ the location of the $k\textrm {th} 0$ . Let $k_m$ be the smallest number such that $i_{k_m}-i_{k_{m-1}}$ is odd. Then by definition of $<_E$ ,

$$ \begin{align*}\sigma^{i_{k_{m-1}}-1}(w^\infty)>_E10\cdot 1^\infty.\\[-36pt]\end{align*} $$

Remark 3.5. By $k\textrm {th}$ renormalization or $k\textrm {th}$ doubling, we mean carrying out the renormalization or doubling on a word or sequence k times. Proposition 3.3 above implies that if $w'$ is the $k\textrm {th}$ renormalization of w, then the roots of $P_w$ not on the unit circle are the $(2^k)\textrm {th}$ roots of the roots of $P_{w'}$ that are not on the unit circle.

Furthermore, because renormalization of sequences preserves $<_E$ (Lemma 3.1), we can apply Proposition 3.4 above repeatedly to show that if the $w_k$ is the $k\textrm {th}$ doubling of $10\cdot 1^\infty $ , w is admissible, and $w^\infty <_Ew_k$ , then w has a $k\textrm {th}$ renormalization.

4 Roots in $\mathbb {D}$ of reducible Parry polynomials

The purpose of this section is to prove Theorem 4.5, an alternative characterization of sets ${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$ , for $\unicode{x3bb} \in (1,2]$ , using the results in [BDLW19]. An upshot of Theorem 4.5 is that we do not need to worry about extraneous roots in $\mathbb {D}$ from reducible Parry polynomials.

We will use the following four results from [BDLW19].

Theorem 4.1. [BDLW19, Theorem 1 (‘persistence theorem’), Theorem 2]

If $(z, \unicode{x3bb} )\in {\Upsilon _2^{cp}}$ , $|z|\leq 1$ , then so is $(z, y)$ for any $y\in [\unicode{x3bb} , 2]$ .

Proposition 4.2. [BDLW19, Lemma 5.3]

Let $w_1$ be dominant, $w_1>_E10\cdot 1^{|w_1|-2}$ , $w_2$ be admissible, $w_1^\infty>_Ew_2^\infty $ , and assume that there is some m such that

$$ \begin{align*}2m|w_2|>|w_1|>m|w_2|.\end{align*} $$

Then there is some $w'$ , some integer $m'\geq m$ , such that $(w_1w'w_2^{m'})^\infty $ is admissible,

$$ \begin{align*}|w_1|+|w'|\geq m'|w_2|,\end{align*} $$

and the Parry polynomial $P_{w_1w'w_2^{m'}}(z)$ can be written as the product of $(z-1)$ and another polynomial $Q(z)$ such that $Q(z^{2^k})$ is irreducible for all integers $k \geq 0$ .

Proposition 4.3. [BDLW19, Lemma 5.5]

If $w_2$ is an admissible word and $z\in \mathbb {D}$ is a root of $P_{w_2}$ , then for any $\epsilon>0$ , there exists $N\in \mathbb {N}$ such that for any word $w_1$ and any integer $n\ge N$ , $P_{w_1w_2^n}$ has a root within distance $\epsilon $ of z.

Proposition 4.4. [BDLW19, Lemma 5.7, Remark 5.8]

If $y\in [\sqrt {2}, 2]$ , for any $\epsilon>0$ , there exists a dominant word $w_1$ such that for any word $w_2$ , the leading root of $P_{w_1w_2}$ is within distance $\epsilon $ of y, and $w_1>_E10\cdot 1^{|w_1|-2}$ .

We now use the above results to establish the following characterization of the sets ${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$ , which will be the starting point of our proof of Theorem 1.7.

Theorem 4.5. Fix $1 < \unicode{x3bb} < 2$ . For each $\unicode{x3bb} '> \unicode{x3bb} $ , define $Y_{\unicode{x3bb} '}$ to be the closure of the set of roots in $\overline {\mathbb {D}}$ of all Parry polynomials $P_w$ such that w is admissible and $w^\infty \leq _E\mathrm {{It}}_{\unicode{x3bb} '}$ , union with $S^1$ , that is,

$$ \begin{align*}Y_{\unicode{x3bb}'} := S^1 \cup \overline{ \{z \in \overline{\mathbb{D}} : P_w(z) = 0 \textrm{ for some admissible word } w \textrm{ such that } w^\infty \leq_E\mathrm{{It}}_{\unicode{x3bb}'}\} }.\end{align*} $$

Then,

$$ \begin{align*}{\Xi}_{\unicode{x3bb}}\cap \overline{\mathbb{D}} = \bigcap_{\unicode{x3bb}'> \unicode{x3bb}} Y_{\unicode{x3bb}'}.\end{align*} $$

Remark 4.6. The condition ‘ $w^\infty <_E\mathrm {{It}}_{\unicode{x3bb} '}$ for every $\unicode{x3bb} '>\unicode{x3bb} $ ’ is different from ‘ $w^{\infty } \leq \mathrm {{It}}_{\unicode{x3bb} }$ ’ because there could exist a symbolic coding for the itinerary of $1$ under the tent map $f_{\unicode{x3bb} }$ that is $>_E \mathrm {{It}}_{\unicode{x3bb} }$ .

Proof. For any $1 < \unicode{x3bb} < 2$ , let

$$ \begin{align*}{\Xi}^{\prime}_\unicode{x3bb} = \bigcap_{\unicode{x3bb}'> \unicode{x3bb}} Y_{\unicode{x3bb}'}.\end{align*} $$

We will first prove ${\Xi }_{\unicode{x3bb} } \subseteq {\Xi }_{\unicode{x3bb} }'$ . For any $\unicode{x3bb} '$ , define the set $Z_{\unicode{x3bb} '}$ to be the closure of the set of Galois conjugates of critically periodic growth rates that are at most $\unicode{x3bb} '$ , union with $S^1$ . By the persistence theorem, $\unicode{x3bb} _1 < \unicode{x3bb} _2$ implies $Z_{\unicode{x3bb} _1} \subseteq Z_{\unicode{x3bb} _2}$ . So if any point $x \in \bigcap _{\unicode{x3bb} '> \unicode{x3bb} } Z_{\unicode{x3bb} '}$ , then $x \in {\Xi }_{\unicode{x3bb} }$ since $\Upsilon _2^{cp}$ is closed; similarly, if $x \not \in \bigcap _{\unicode{x3bb} '> \unicode{x3bb} } Z_{\unicode{x3bb} '}$ , then $x \not \in {\Xi }_{\unicode{x3bb} }$ . Hence,

$$ \begin{align*}{\Xi}_{\unicode{x3bb}}\cap\overline{\mathbb{D}} = \bigcap_{\unicode{x3bb}'> \unicode{x3bb}} Z_{\unicode{x3bb}'}.\end{align*} $$

The conclusion will now follow from the statement that $Z_{\unicode{x3bb} '} \subseteq Y_{\unicode{x3bb} '}$ for all $\unicode{x3bb} '$ . If z is a Galois conjugate of a critically periodic growth rate $\unicode{x3bb} "$ that is at most $\unicode{x3bb} '$ , then z is a root of the Parry polynomial $P_w$ such that $w^{\infty }=\mathrm {{It}}_{\unicode{x3bb} "}$ , and $\mathrm {{It}}_{\unicode{x3bb} "} \leq _E \mathrm {{It}}_{\unicode{x3bb} '}$ by Corollary 2.4. Thus, $Z_{\unicode{x3bb} '} \subseteq Y_{\unicode{x3bb} '}$ for all $\unicode{x3bb} '$ .

We will now prove ${\Xi }^{\prime }_\unicode{x3bb} \subseteq {\Xi }_\unicode{x3bb} $ . To do this, it suffices to show

$$ \begin{align*}Y_{\unicode{x3bb}'} \subseteq \bigcap_{\unicode{x3bb}"> \unicode{x3bb}'} Z_{\unicode{x3bb}"}.\end{align*} $$

We first consider the case $\unicode{x3bb} '\geq \sqrt {2}$ . Suppose z is the root of some $P_w$ , where w is admissible and the leading root of $P_w$ is no larger than $\unicode{x3bb} '$ . ( $Y_{\unicode{x3bb} '}$ is the closure of all such z terms.) For any $\epsilon>0$ , Proposition 4.4 guarantees the existence of a dominant word $w_1$ such that for any $w_2$ , the leading root of $P_{w_1w_2}$ is in $[\unicode{x3bb} ', \unicode{x3bb} '+\epsilon )$ and $w_1>_E10\cdot 1^{|w_1|-2}$ . By monotonicity (Corollary 2.4), $w_1^{\infty }>_E w^{\infty }$ . Without loss of generality, we may choose $w_1$ so that its length, $|w_1|$ , is arbitrarily big (this is because as we let $\epsilon \to 0$ , we get arbitrarily many such dominant strings, and there are finitely many strings of at most any given length). Thus we may assume that $w_1$ and w satisfy the assumptions of Proposition 4.2 with the m of Proposition 4.2 being arbitrarily large, and in particular, m is $\geq $ the N of Proposition 4.3 using w for $w_2$ . Let $w_3$ be the word constructed by Proposition 4.2. Because $w_3$ is admissible, has positive cumulative sign, and $P_{w_3}(z)/(z-1)$ is irreducible, $w_3^{\infty } = \mathrm {{It}}_{\unicode{x3bb} _3}$ for some $\unicode{x3bb} _3$ by Proposition 2.3. We know $\unicode{x3bb} _3 \in [\unicode{x3bb} ', \unicode{x3bb} '+\epsilon ]$ because $w_3$ has the prefix $w_1$ . Also, any root of $P_{w_3}$ in $\mathbb {D}$ will be a Galois conjugate of $\unicode{x3bb} _3$ , and by construction, $P_{w_3}$ has a root close to z. The containment now follows from letting $\epsilon \rightarrow 0$ .

Now we deal with the case $1<\unicode{x3bb} '<\sqrt {2}$ . Let k be the unique natural number such that $(\unicode{x3bb} ')^{2^k}\in [\sqrt {2}, 2)$ . Remark 3.5 implies that w has a $k\textrm {th}$ renormalization $w_0$ , and $z^{2^k}$ is a root of $P_{w_0}$ . Using $w_0$ in place of w in the argument in the previous paragraph, we get a critically periodic growth rate $\unicode{x3bb} _4$ close to $(\unicode{x3bb} ')^{2^k}$ , such that one of its Galois conjugates $z_2$ is close to $z^{2^k}$ . The conclusion in Proposition 4.2 further implies that any $(2^k)\textrm {th}$ root of $z_2$ must be a Galois conjugate of the $(2^k)\textrm {th}$ root of $\unicode{x3bb} _4$ as well, which implies that there is a Galois conjugate of $\unicode{x3bb} _4^{2^{-k}}$ which is close to z, which finishes the proof of the proposition.

The following corollary is not used to prove any further results in the present work.

Corollary 4.7. Let V denote the set of all real numbers $\unicode{x3bb} \in (1,2)$ such that:

1. (1) the tent map $f_{\unicode{x3bb} }$ is critically periodic;

2. (2) there exists a word w such that $\mathrm {{It}}_{\unicode{x3bb} } = w^{\infty }$ ;

3. (3) the Parry polynomial $P_w(z)$ can be written as the product of an irreducible polynomial (in $\mathbb {Z}[z]$ ) and some cyclotomic polynomials.

Then V is dense in $[1,2]$ .

Proof. The growth rates $\unicode{x3bb} _3$ , as well as the growth rates $\unicode{x3bb} _3^{2^{-k}}$ , $k \in \mathbb {N}$ , constructed in the proof of Theorem 4.5 all satisfy conditions (1)–(3).

5 $\unicode{x3bb} $ -suitability

In this section, we establish some basic properties of $\unicode{x3bb} $ -suitability and prove the technical lemmas about $\unicode{x3bb} $ -suitability that we will need in §6.

For convenience, we reproduce the definition of $\unicode{x3bb} $ -suitability here. For $\unicode{x3bb} \in (1,2)$ , a sequence w is called $\unicode{x3bb} $ -suitable if for every $\unicode{x3bb} '\in (\unicode{x3bb} , 2]$ , the following conditions hold.

1. (1) ${\textrm {Rev}} ( {\textrm {Pre}}_n(w)) \leq _E {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$ for all $n \in \mathbb {N}$ .

2. (2) If ${\textrm {Rev}}({\textrm {Pre}}_n(w)) = {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$ , then the cumulative sign $s({\textrm {Pre}}_n(w)) = -1$ .

3. (3) If $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots , k \in \mathbb {N}$ , then w does not contain $k+1$ consecutive $0$ s (that is, if $\mathrm {{It}}_{\unicode{x3bb} '}$ starts with $1$ followed by $k 0$ s and then $1$ , writing w as $w=w_1w_2\ldots ,$ there does not exist $n \in \mathbb {N}$ such that $w_i = 0$ for all $n \leq i \leq n+k$ ).

4. (4) If $n \in \mathbb {N}$ satisfies $\sqrt {2} \leq _E (\unicode{x3bb} ')^{2^n} < 2$ , then $w = \mathfrak {D}^{\prime {n}}(w')$ for some sequence $w'$ , where $\mathfrak {D}'$ is the map that replaces $0$ with $11$ and $1$ with $01$ . Furthermore, if

   $$ \begin{align*}\mathrm{{It}}_{\unicode{x3bb}^{\prime2^n}} = 1\cdot 0^k \cdot1\ldots,\end{align*} $$
   then $w'$ does not contain $k+1$ consecutive $0$ s.

The intuition behind the definition of $\unicode{x3bb} $ -suitability is that we need a condition on sequences w so that Lemma 5.7 works.

Remark 5.1. An immediate consequence of monotonicity (Corollary 2.4) is that if $\unicode{x3bb} '$ satisfies conditions (1)–(4) of Definition 1.5 for a sequence w, then so does every $\unicode{x3bb} "> \unicode{x3bb} '$ .

Remark 5.2. Every itinerary $\mathrm {{It}}_{\unicode{x3bb} '}$ is admissible (by Theorem 2.2), so the admissibility condition implies that if $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots $ , then $\mathrm {{It}}_{\unicode{x3bb} }$ does not contain $k+1$ consecutive $0$ s.

Remark 5.3. Note that the map $\frak {D}'$ defined in the definition of $\unicode{x3bb} $ -suitability is related to the doubling map $\frak {D}$ by

$$ \begin{align*}{\textrm{Rev}} \circ {\textrm{Pre}}_{2n} \circ \frak{D} = \frak{D}' \circ {\textrm{Rev}} \circ {\textrm{Pre}}_n (w)\end{align*} $$

for every sequence w and $n \in \mathbb {N}$ . (Recall that $\frak {D}$ is replacing $0$ with $11$ , $1$ with $10$ , while $\frak {D}'$ is replacing $0$ with $11$ , $1$ with $01$ .)

Lemma 5.4. The set of $\unicode{x3bb} $ -suitable sequences is closed.

Proof. We will show that the set of all sequences that are not $\unicode{x3bb} $ -suitable is open. To do this, it suffices to show that given any sequence w which is not $\unicode{x3bb} $ -suitable, we can find a prefix of w such that every sequence that shares this prefix is not $\unicode{x3bb} $ -suitable. It is clear that conditions (1) and (2) are closed conditions. For condition (3), we choose the prefix to be one that contains the first $k+1$ consecutive $0$ s. Condition (4) is similar.

The following lemma is immediate because the definition of $\unicode{x3bb} $ -suitability is of the form ‘for all $\unicode{x3bb} '> \unicode{x3bb} $ , $P(w,\unicode{x3bb} ')$ ,’ where P is a predicate.

Lemma 5.5. Let $\mathcal {M}_\unicode{x3bb} $ denote the set of $\unicode{x3bb} $ -suitable sequences. Then,

$$ \begin{align*}\mathcal{M}_\unicode{x3bb}=\bigcap_{\unicode{x3bb}" \in (\unicode{x3bb},2]}\mathcal{M}_{\unicode{x3bb}"}.\end{align*} $$

Lemma 5.6. If w is an admissible word that satisfies $w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} }$ for $\unicode{x3bb} \in (1,2)$ , then $(\mathrm {{Rev}}(w))^{\infty }$ is $\unicode{x3bb} $ -suitable.

Proof. Observe that for any $n \in \mathbb {N}$ , if we pick some $k\in \mathbb {N}$ such that $n+k$ is some multiple of $|w|$ , then we have

(5.1) $$ \begin{align} {\textrm{Rev}} ( {\textrm{Pre}}_n({\textrm{Rev}}(w)^{\infty}))) = {\textrm{Pre}}_n(\sigma^{k}(w^{\infty})). \end{align} $$

Since w is admissible, ${\textrm {Pre}}_n(\sigma ^k(w^{\infty })) \leq _E {\textrm {Pre}}_n(w^{\infty })$ for all $k,n \in \mathbb {N}$ . By Corollary 2.4, for any $\unicode{x3bb} '> \unicode{x3bb} $ ,

(5.2) $$ \begin{align} \mathrm{{It}}_{\unicode{x3bb}} <_E \mathrm{{It}}_{\unicode{x3bb}'}. \end{align} $$

We thus have that for any $n \in \mathbb {N}$ ,

$$ \begin{align*} {\textrm{Rev}} ( {\textrm{Pre}}_n({\textrm{Rev}}(w)^{\infty})) = {\textrm{Pre}}_n(\sigma^{k}(w^{\infty})) \leq_E {\textrm{Pre}}_n(w^{\infty}) \leq_E {\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}}) \leq_E {\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}'}), \end{align*} $$

which is condition (1) of the definition of $\unicode{x3bb} $ -suitability.

Now suppose that for some $\unicode{x3bb} '> \unicode{x3bb} $ ,

$$ \begin{align*}{\textrm{Rev}} ( {\textrm{Pre}}_n({\textrm{Rev}}(w)^{\infty}) = {\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}'})\end{align*} $$

and ${\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$ has a positive cumulative sign. Then from (5.1), we have

$$ \begin{align*}{\textrm{Pre}}_n(\sigma^{k}(w^{\infty})) = {\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}'}).\end{align*} $$

Admissibility of w and (5.2) together imply that

(5.3) $$ \begin{align} \sigma^{k}(w^{\infty})\leq_E w^{\infty}<_E\mathrm{{It}}_{\unicode{x3bb}'}. \end{align} $$

Because ${\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$ is the common prefix of $\sigma ^{k}(w^{\infty })$ and $\mathrm {{It}}_{\unicode{x3bb} '}$ , (5.3) implies it must also be a prefix of $w^\infty $ . Removing this common n-prefix with positive cumulative sign from both sides of the inequality (by applying $\sigma ^n$ ) yields

$$ \begin{align*}w^\infty\leq_E\sigma^{n}(w^\infty).\end{align*} $$

However, admissibility also implies that $\sigma ^{n}(w^\infty )\leq w^\infty $ , so in fact

$$ \begin{align*}w^\infty = \sigma^{n}(w^\infty).\end{align*} $$

Therefore,

(5.4) $$ \begin{align} w^\infty=({\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}'}))^{\infty}. \end{align} $$

Let j be the index of the first place $w^{\infty }$ differs from $\mathrm {{It}}_{\unicode{x3bb} '}$ . Clearly, $j>n$ . Pick $m \in \mathbb {N}$ such that $mn<j\leq (m+1)n$ . Then, after removing the common prefix of length $mn$ and positive cumulative sign from both $w^{\infty }$ and $\mathrm {{It}}_{\unicode{x3bb} '}$ , we get from (5.4) and (5.2) that

$$ \begin{align*}\sigma^{mn}(w^{\infty}) = w^{\infty}<_E \mathrm{{It}}_{\unicode{x3bb}'},\end{align*} $$

and hence,

$$ \begin{align*}{\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}'})={\textrm{Pre}}_n(w^\infty)<_E{\textrm{Pre}}_n(\sigma^{mn}(\mathrm{{It}}_{\unicode{x3bb}'})),\end{align*} $$

which contradicts with the fact that $\mathrm {{It}}_{\unicode{x3bb} '}$ is admissible (by Theorem 2.2). Thus, condition (2) of the definition of $\unicode{x3bb} $ -suitability holds.

Now condition (3) of the definition of $\unicode{x3bb} $ -suitability follows from the assumption that $w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} }$ .

For condition (4), suppose for some $\unicode{x3bb} '>\unicode{x3bb} $ , $\sqrt {2}\leq (\unicode{x3bb} ')^{2^n}<2$ . Then $\unicode{x3bb} ^{2^n}<2$ , so by Lemma 3.4, $w=\mathfrak {D}^n(w')$ for some $w'$ . Hence,

$$ \begin{align*}({\textrm{Rev}}(w))^\infty=(\mathfrak{D}^{\prime{n}}({\textrm{Rev}}(w'))^\infty.\end{align*} $$

Because $\mathfrak {D}$ preserves $\leq _E$ and sends itineraries to itineraries (Lemma 3.2), the number of consecutive $0$ s in $({\textrm {Rev}}(w'))^\infty $ , which is the number of consecutive $0$ s in $w^{\prime \infty }$ , cannot be more than the number of consecutive $0$ s in $\mathrm {{It}}_{\unicode{x3bb} ^{\prime 2^n}}$ .

The key combinatorial result we need to prove Theorem 1.7 is the following.

Lemma 5.7. Fix $\unicode{x3bb} \in [1,2)$ and let $w_0$ be a finite dominant word such that $\mathrm {{It}}_{\unicode{x3bb} '}\leq _E w_0^\infty $ for some $\unicode{x3bb} '>\unicode{x3bb} $ . Let $\alpha $ be a word such that $\alpha $ :

1. (1) ends with $1$ ;

2. (2) is a prefix of some $\unicode{x3bb} $ -suitable sequence;

3. (3) has positive cumulative sign; and

4. (4) $|w_0|>|\alpha |$ .

Then the word $w_0\cdot \mathrm {{Rev}}(\alpha )$ is admissible.

Proof. Let $\alpha '={\textrm {Rev}}(\alpha )$ . It suffices to show that the admissibility criterion

$$ \begin{align*}\sigma^k((w_0\alpha')^\infty)\leq_E (w_0\alpha')^\infty\end{align*} $$

holds for all $1\leq k< |\alpha |+|w_0|$ .

Case 1: $k<|w_0|$ . This implies that the comparison between $\sigma ^k((w_0\alpha ')^\infty )$ and $(w_0\alpha ')^\infty $ is equivalent to the comparison of a proper suffix of $w_0$ concatenated with $1$ with a prefix of $w_0$ of the same length. Hence,

$$ \begin{align*}\sigma^k((w_0\alpha')^\infty)\leq_E (w_0\alpha')^\infty\end{align*} $$

because $w_0$ is dominant.

Case 2: $|w_0|\leq k < |\alpha |+|w_0|$ . Suppose the first place $\sigma ^k((w_0\alpha ')^\infty )$ and $(w_0\alpha ')^\infty $ differ is at the $j\textrm {th}$ position. It is evident that $1\leq j\leq |\alpha |+|w_0|$ . We divide this into two subcases.

Case 2A: $j\leq |w_0|+|\alpha |-k$ . The fact that $|w_0|>|\alpha |$ and $k\geq |w_0|$ implies that $j\leq |w_0|$ . Hence, the comparison between $\sigma ^k((w_0\alpha ')^\infty )$ and $(w_0\alpha ')^\infty $ is equivalent to the comparison of a proper suffix of $\alpha '$ with a prefix of $w_0$ . Hence, item (1) of Definition 1.5 gives us

$$ \begin{align*}\sigma^k((w_0\alpha')^\infty)\leq_E (w_0\alpha')^\infty.\end{align*} $$

Case 2B: $j>|w_0|+|\alpha |-k$ . The word $\beta :={\textrm {Suf}}_{|w_0|+|\alpha |-k}(\alpha ')$ , which is a common prefix of $\sigma ^k((w_0\alpha ')^\infty )$ and $(w_0\alpha ')^\infty $ , is identical to a prefix of $w_0$ , which is $\ge _E$ than a prefix of $\mathrm {{It}}_{\unicode{x3bb} '}$ for some $\unicode{x3bb} '>\unicode{x3bb} $ . Hence, due to item (2) of Definition 1.5, $\beta $ has a negative cumulative sign. Now, using the conclusion of Case 1, we have

$$ \begin{align*}\sigma_k^{|w_0|+|\alpha|-k}(\sigma^k((w_0\alpha')^\infty))=(w_0\alpha')^\infty>_E \sigma_k^{|w_0|+|\alpha|-k}((w_0\alpha')^\infty).\end{align*} $$

Hence,

$$ \begin{align*}\sigma^k((w_0\alpha')^\infty)\leq_E (w_0\alpha')^\infty\end{align*} $$

because $\beta $ has a negative cumulative sign.

Lemma 5.8. Let w and $w'$ be sequences, and let $\unicode{x3bb} {\kern-1pt}\in{\kern-1pt} (1,2)$ and $k {\kern-1pt}\in{\kern-1pt} \mathbb {N}$ satisfy $\sqrt {2}{\kern-1pt} \leq{\kern-1pt} \unicode{x3bb} ^{2^k} {\kern-2pt}<{\kern-1pt} 2$ . If w is $\unicode{x3bb} $ -suitable and $w = \mathfrak {D'}^k(w')$ , then $w'$ is $\unicode{x3bb} ^{2^k}$ -suitable.

Proof. By induction, we only need to prove it for $k=1$ . Assume $w=\mathfrak {D'}(w')$ is $\unicode{x3bb} $ -suitable, we will now show that $w'$ satisfies conditions (1)–(4) of Definition 1.5. By definition,

$$ \begin{align*}{\textrm{Rev}}(\mathfrak{D'}(v))=\mathfrak{D}({\textrm{Rev}}(v))\end{align*} $$

for any word v, so for any $\unicode{x3bb} '>\unicode{x3bb} $ ,

$$ \begin{align*}{\textrm{Rev}}({\textrm{Pre}}_{2n}(\mathfrak{D'}(w'))={\textrm{Rev}}(\mathfrak{D'}({\textrm{Pre}}_n(w')))\end{align*} $$

$$ \begin{align*}=\mathfrak{D}({\textrm{Rev}}({\textrm{Pre}}_n(w')))\leq {\textrm{Pre}}_{2n}(\mathrm{{It}}_{\unicode{x3bb}'})=\mathfrak{D}({\textrm{Pre}}_n(\mathrm{{It}}_{\unicode{x3bb}^{\prime2}})).\end{align*} $$

Hence condition (1) is true for $w'$ because of Lemmas 3.1 and 3.2. Condition (2) of Definition 1.5 can be verified similarly. It is easy to see that w satisfies condition (4) implies that $w'$ satisfies condition (4). Lastly, we will now show that w satisfies condition (4) will imply $w'$ satisfies condition (3): if $\unicode{x3bb} ^2\geq \sqrt {2}$ , this follows from the statement of condition (4). If $\unicode{x3bb} ^2<\sqrt {2}$ , condition (4) implies that $w'=\mathfrak {D'}(w")$ for some $w"$ , which implies that $w'$ can never have more than one consecutive 0, and hence it also satisfies condition (3).

6 Characterization inside the unit cylinder

Lemma 6.1. Let $\mathcal {K}$ denote the space of compact subsets of $\mathbb {R}^3$ with the Hausdorff metric topology. Given any compact subset K of $\mathcal {K}$ , the union of the elements of K is a compact subset of $\mathbb {R}^3$ .

Proof. First, we claim there exists $R>0$ such that $k \subset \overline {B_R(0)}$ for all $k \in K$ . If this was not the case, then there exist $k_1$ and $k_2$ in K such that $d_{\textrm {Haus}}(k_1,k_2)$ is arbitrarily large, contradicting the fact that K is compact. Thus the claim is true.

Consider $K \times \overline {B_R(0)}$ . As a product of compact sets, it is compact. Consider the subset $C \subseteq K$ such that C consists of all pairs $(k,x)$ such that $x \in k$ . We claim C is closed, and thus as a closed subset of a compact set, C is compact. To see this, we will show that C is sequentially closed, that is, if $(k_i,x_i)$ is a sequence in C converging to $(k_{\infty },x_{\infty }) \in K \times \overline {B_R(0)}$ , then $(k_{\infty },x_{\infty }) \in C$ . We have that $k_i \to k_{\infty }$ and $x_i \to x_{\infty }$ , so suppose $x_{\infty } \not \in k_{\infty }$ . Since $k_{\infty }$ is a compact set, $x \not \in k_{\infty }$ implies there exists $\epsilon> 0$ such that $B_{\epsilon }(x)$ is contained in the complement of $k_{\infty }$ . This implies that $\liminf d_{\textrm {Haus}}(k_i,k_{\infty }) \geq \epsilon $ , contradicting the fact that $k_i \to k_{\infty }$ in the Hausdorff metric. So we have a continuous map from C to $\mathbb {R}^3$ sending $(k,x)$ to x. The image under this map is compact.

The following two lemmas, which we state without proof, are immediate consequences of Rouché’s theorem.

Lemma 6.2. Let $M>0$ be some fixed number. Let A be the set of power series with coefficients bounded by M equipped with the product topology. Let $\mathcal {C}$ be the set of compact subsets of $\mathbb {C}$ equipped with the Hausdorff topology. Then the map $\rho :A \to \mathcal {C}$ defined by

$$ \begin{align*}\rho(f) = S^1 \cup \{z \in \mathbb{D} : f(z) = 0\}\end{align*} $$

is continuous.

Lemma 6.3. Fix real numbers $M>0$ , $0<r<1$ , $\epsilon>0$ . Suppose $\alpha $ is a power series whose coefficients are all bounded in absolute value by M. Then there exists a real number $N = N(\alpha ,r,\epsilon ,M)$ such that for every power series $\beta $ , whose coefficients are all bounded in absolute value by M and whose first N terms equal the first N terms of $\alpha $ , for each root z of $\alpha $ with $|z|<r$ , there exists a root $z'$ of $\beta $ such that $|z-z'|<\epsilon $ .

Now we prove the first main theorem.

Proof of Theorem 1.7

For the reader’s convenience, we reproduce here the statement of Theorem 1.7. For any $\unicode{x3bb} \in (1,2]$ ,

$$ \begin{align*}{\Xi}_\unicode{x3bb} \cap \overline{\mathbb{D}} = S^1\cup \{z\in\mathbb{D}: G(w, z)=1\text{ for some }\unicode{x3bb}\text{-suitable sequence }w \}.\end{align*} $$

By Remark 1.11, the result holds for $\unicode{x3bb} =2$ . So fix $\unicode{x3bb} \in (1,2)$ . For brevity, let

$$ \begin{align*}Z_\unicode{x3bb}:=\{z\in \mathbb{D}: G(w, z)=1\text{ for some }\unicode{x3bb}\text{-suitable sequence }w\}.\end{align*} $$

First, we show that $S^1\cup Z_\unicode{x3bb} $ is compact. For each sequence w, the function from $\mathbb {D}$ to $\mathbb {C}$ given by $z \mapsto G(w, \cdot )-1$ is a power series with bounded coefficients. Furthermore, the map from the set of sequences w (with the product topology) to the set of power series (with the product topology on coefficients) given by $w \mapsto G(w,\cdot )-1$ is continuous. Therefore, Lemma 6.2 implies that the map $\rho $ from the set of sequences with the product topology to $\mathcal {C}$ , the set of compact subsets of $\mathbb {C}$ with the Hausdorff topology, given by

$$ \begin{align*}\rho(w) = S^1 \cup \{z \in \mathbb{D} : G(w,z) = 1\},\end{align*} $$

is continuous. By Lemma 5.4, the set of all $\unicode{x3bb} $ -suitable sequences is closed (in the product topology on the set of sequences), and hence compact. Therefore, since $\rho $ is continuous,

$$ \begin{align*}\{\rho(w) : w \textrm{ is } \unicode{x3bb}-\textrm{suitable}\}\end{align*} $$

is a compact subset of $\mathcal {C}$ . Hence, Lemma 6.1 implies that

$$ \begin{align*}\bigcup_{w\text{ is }\unicode{x3bb}\text{-suitable}}\rho(w)\end{align*} $$

is compact. However, this set is precisely $S^1\cup Z_\unicode{x3bb} $ , so we have shown $S^1\cup Z_\unicode{x3bb} $ is compact for any $\unicode{x3bb} \in [1,2]$ .

Next, we show that

$$ \begin{align*}{\Xi}_\unicode{x3bb}\cap \overline{\mathbb{D}}\subseteq S^1\cup Z_\unicode{x3bb}.\end{align*} $$

Theorem 4.5 shows that

(6.1) $$ \begin{align} {\Xi}_\unicode{x3bb}\cap \overline{\mathbb{D}}=\bigcap_{\unicode{x3bb}'>\unicode{x3bb}}Y_{\unicode{x3bb}'}, \end{align} $$

where $Y_{\unicode{x3bb} '}$ is defined to be the closure of the set of roots in $\overline {\mathbb {D}}$ of all Parry polynomials $P_w$ such that w is admissible and $w^\infty \leq _E\mathrm {{It}}_{\unicode{x3bb} '}$ , union with $S^1$ . For each such w, let $w_r$ be the sequence

$$ \begin{align*}w_r :=({\textrm{Rev}}(w))^\infty.\end{align*} $$

So fix $\unicode{x3bb} '> \unicode{x3bb} $ and consider any admissible word w such that $w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} '}$ . By Lemma 2.1,

$$ \begin{align*}P_w(z) = (1-z^{|w|})G(w_r,z).\end{align*} $$

By Lemma 5.6, $w_r$ is $\unicode{x3bb} '$ -suitable. Hence, all roots in $\overline {\mathbb {D}}$ of $P_w$ are in $S^1 \cup Z_{\unicode{x3bb} '}$ . Then, since $Z_{\unicode{x3bb} '}$ is closed, we have that

(6.2) $$ \begin{align} Y_{\unicode{x3bb}'}\subseteq S^1\cup Z_{\unicode{x3bb}'}. \end{align} $$

Now, combining (6.1) and (6.2) shows that for any point $z\in {\Xi }_\unicode{x3bb} \cap \mathbb {D}$ , for each $n\in \mathbb {N}$ , there exists a $(\unicode{x3bb} +{1/n})$ -suitable sequence $v_n$ such that $G(v_n, z)=1$ . Let $v_\infty $ be an accumulation point of the set $\{v_n : n \in \mathbb {N}\}$ . By Lemma 5.5, the sequence $v_\infty $ is $\unicode{x3bb} $ -suitable. The continuity of $w\mapsto G(w, \cdot )$ implies that $G(v_\infty , z)=1$ . Hence, ${\Xi }_{\unicode{x3bb} }\cap \overline {\mathbb {D}}\subseteq S^1\cup Z_{\unicode{x3bb} }$ .

Lastly, we show that $S^1\cup Z_\unicode{x3bb} \subseteq {\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}.$ We know from [BDLW19] that $S^1 \times [1,2] \subset \Upsilon _2^{cp}$ . Thus, $S^1\subset {\Xi }_\unicode{x3bb} $ , so it suffices to show that $Z_\unicode{x3bb} \subset {\Xi }_{\unicode{x3bb} }$ . Fix a point $z\in Z_\unicode{x3bb} $ and let w be a $\unicode{x3bb} $ -suitable sequence such that $G(w, z)=1$ . By condition (4) of Definition 1.5, there exists a sequence $w'$ such that $w=\mathfrak {D'}^k(w')$ , and by Lemma 5.8, $w'$ is $\unicode{x3bb} ^{2^k}$ -suitable and $\unicode{x3bb} ^{2^k}\geq \sqrt {2}$ . In particular, if $\unicode{x3bb} \geq \sqrt {2}$ , we can let $k=0$ and $w'=w$ . As a consequence, there are infinitely many prefixes of $w'$ that end with $1$ and have a positive cumulative sign.

For any $m \in \mathbb {N}$ such that ${\textrm {Pre}}_m(w')$ has a positive cumulative sign and any word $w"$ with a positive cumulative sign, it follows immediately from the definitions of a Parry polynomial and of G that the first m terms of the power series $G(w', z)-1$ and $P_{w" \cdot {\textrm {Rev}}({\textrm {Pre}}_m(w'))}(z)$ agree. Therefore, for any fixed $\epsilon _1>0$ , by Lemma 6.3, there exists $N \in \mathbb {N}$ such that ${\textrm {Pre}}_N(w')$ ends with $1$ and has a positive cumulative sign, and for any word $w"$ with a positive cumulative sign, there exists a point $z' \in B_{\epsilon _1}(z^{2^k})$ such that

(6.3) $$ \begin{align} P_{w"\cdot {\textrm{Rev}}({\textrm{Pre}}_N(w'))}(z')=0. \end{align} $$

For any fixed $\unicode{x3bb} '$ satisfying $2> \unicode{x3bb} ' > \unicode{x3bb} ^{2^k}$ , pick a critically periodic growth rate $\unicode{x3bb} " \in (\unicode{x3bb} ^{2^k},\unicode{x3bb} ')$ and word $w_0$ with a positive cumulative sign such that $\mathrm {{It}}_{\unicode{x3bb} "}=w_0^{\infty }$ . Since $\unicode{x3bb} " < \unicode{x3bb} '$ , for sufficiently large n,

$$ \begin{align*}w_0^n <_E {\textrm{Pre}}_{n|w_0|}(\mathrm{{It}}_{\unicode{x3bb}'}).\end{align*} $$

Hence, by Proposition 2.5, there exists $n \in \mathbb {N}$ and a word $w_1'$ such that the word

$$ \begin{align*}w_1:= w_0^nw^{\prime}_1\end{align*} $$

is dominant, $|w_1|> |w'|$ , and

(6.4) $$ \begin{align} w_1<_E{\textrm{Pre}}_{|w_1|}(\mathrm{{It}}_{\unicode{x3bb}'}). \end{align} $$

By Lemma 5.7,

$$ \begin{align*}w_1 \cdot {\textrm{Rev}}({\textrm{Pre}}_N(w))'\end{align*} $$

is admissible. By (6.3),

$$ \begin{align*}P_{w_1\cdot {\textrm{Rev}}({\textrm{Pre}}_N(w'))}\end{align*} $$

has a root within distance $\epsilon _1$ of $z^{2^k}$ . By (6.4),

$$ \begin{align*}(w_1\cdot {\textrm{Rev}}({\textrm{Pre}}_N(w')))^\infty<_E \mathrm{{It}}_{\unicode{x3bb}'}.\end{align*} $$

Hence, the $k\textrm {th}$ doubling of $w_1\cdot {\textrm {Rev}}({\textrm {Pre}}_N(w'))$ , denoted as $w_d$ , satisfies

$$ \begin{align*}w_d^\infty<_E\mathrm{{It}}_{(\unicode{x3bb}')^{1/2^k}}\end{align*} $$

and $P_{w_d}$ has leading root in $[\unicode{x3bb} , (\unicode{x3bb} ')^{1/2^k}]$ and a root in $B_{\epsilon ^{\prime }_1}(z)$ , where $\epsilon ^{\prime }_1$ is the diameter of the preimage of $B_{\epsilon '}(z^{2^k})$ under the map $z\mapsto z^{2^k}$ .

Now, since $\epsilon _1>0$ and $\unicode{x3bb} '>\unicode{x3bb} $ were arbitrary, and since ${\Upsilon _2^{cp}}$ is closed, we obtain that $(z, \unicode{x3bb} )\in {\Upsilon _2^{cp}}$ , and hence $z\in {\Xi }_\unicode{x3bb} $ .

7 Characterization outside the unit cylinder

The goal of this section is to prove Theorem 1.8, a characterization of the part of the Master Teapot that is outside the unit cylinder.

Proof of Theorem 1.8

For any $\unicode{x3bb} \in (1, 2)$ , denote by $f_\unicode{x3bb} $ the $\unicode{x3bb} $ -tent map, and define the set

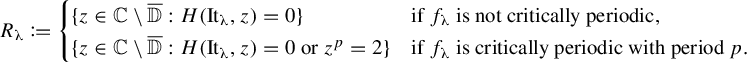
Next, define

We will show that

$$ \begin{align*}R = {\Upsilon_2^{cp}} \cap (\{z : |z| \geq 1\} \times (1,2)).\end{align*} $$

Our argument will almost immediately follow from results in [Tio18], though these results must be translated from the context of the Mandelbrot set to the context of tent maps. The Milnor–Thurston kneading theory [MT88] yields an entropy-preserving semiconjugacy from the set of real quadratic polynomials $f_c$ , $c \in [-2,1/4]$ , to the set of tent maps. If the quadratic $f_c$ is sent by this semiconjugacy to a tent map $f_{\unicode{x3bb} }$ , then $(1-z^{-1})K_c(z^{-1}) = H(\mathrm {It}_{\unicode{x3bb} },z)$ , and hence the roots (in $\mathbb {D}$ ) of the kneading determinant $K_c$ coincide with the reciprocals of the roots (in $\mathbb {C} \setminus \overline {\mathbb {D}}$ ) of $H(\mathrm {It}_{\unicode{x3bb} },z)$ . By [Jun14, Theorem 4.7], on the real slice of the Mandelbrot set, core entropy of $f_c:z \mapsto z^2+c$ is strictly increasing except on ‘small Mandelbrot sets,’ where the core entropy is constant. Consequently, the entropy-preserving semiconjugacy from real quadratics to tent maps is injective except for collapsing each small Mandelbrot set to a single tent map. Furthermore, the semiconjugacy induces a surjection from the set of critically periodic quadratics $f_c$ to the set of critically periodic tent maps, and each small Mandelbrot set contains a critically periodic quadratic.

We will first show that R is a (relatively) closed subset of $\mathbb {C}\times (1, 2)$ . By Proposition 3.3 of [Tio18], the set that is the union of $S^1$ and the roots of $K_c$ varies continuously in the Hausdorff topology with the parameter c. Consequently, when $f_\unicode{x3bb} $ is not critically periodic, the function $s\mapsto R_s\cup S_1$ is continuous at $s=\unicode{x3bb} $ . As stated in the proof of Theorem 7.1 of [Tio18], if $(c_1,c_0)$ is the real section of a small Mandelbrot set of period p, then $K_{c_0}(t) = P_{c_0}(t) / (1-t^p)$ and $K_{c_1}(t) = P_{c_0}(t)(1-2t^p) / (1-t^p)$ . Thus, in the Hausdorff topology,

$$ \begin{align*}\{z \in \mathbb{D} : K_{c_0}(z) = 0 \textrm{ or } z^p = \tfrac{1}{2} \} \cup S^1= \lim_{c_* \nearrow c_1} \{z \in \mathbb{D} : K_{c_*}(z) = 0\} \cup S^1,\end{align*} $$

and so denoting by $\unicode{x3bb} $ the growth rate of $f_{c_0}$ , we have

$$ \begin{align*}\{z \in \mathbb{C} \setminus \overline{\mathbb{D}} : H(\mathrm{It}_{\unicode{x3bb}},z) = 0 \textrm{ or } z^p = 2 \} \cup S^1= \lim_{\unicode{x3bb}_* \searrow \unicode{x3bb}} \{z \in \mathbb{C} \setminus \overline{\mathbb{D}} : H(\mathrm{It}_{\unicode{x3bb}_*},z) = 0\} \cup S^1.\end{align*} $$

Therefore, for any $\unicode{x3bb} $ for which the tent map $f_\unicode{x3bb} $ is critically periodic,

$$ \begin{align*}R_\unicode{x3bb}\cup S^1=\lim_{s\rightarrow \unicode{x3bb}_-}(R_s\cup S^1)\cup \lim_{s\rightarrow \unicode{x3bb}_+}(R_s\cup S^1).\end{align*} $$

Hence, R is a closed subset of $\mathbb {C}\times (1, 2)$ .

When $f_\unicode{x3bb} $ is critically periodic, $H(\mathrm {{It}}_\unicode{x3bb} , z)$ can be written as a rational function with integer coefficients; consequently, $R_{\unicode{x3bb} }$ contains all the Galois conjugates of $\unicode{x3bb} $ in $\mathbb {C} \setminus \mathbb {D}$ . Therefore, for every $\unicode{x3bb} $ such that the tent map $f_{\unicode{x3bb} }$ is critically periodic,

$$ \begin{align*}({\Xi}_\unicode{x3bb}\backslash\mathbb{D})\cup S^1\subseteq R_\unicode{x3bb}\cup S^1.\end{align*} $$

Since ${\Upsilon _2^{cp}} \cap \{z \mid |z| \geq 1\} \times (1,2)$ is formed by taking the closure of the union of all sets $({\Xi }_\unicode{x3bb} \backslash \mathbb {D})\cup S^1$ for $\unicode{x3bb} $ critically periodic, and since R is already closed, this implies

$$ \begin{align*}{\Upsilon_2^{cp}} \cap (\{z : |z| \geq 1\} \times (1,2)) \subseteq R.\end{align*} $$

To show containment in the other direction, Lemma 7.3 in [Tio18] implies that when $f_\unicode{x3bb} $ is not critically periodic, $R_\unicode{x3bb} \times \{\unicode{x3bb} \}\subset {\Upsilon _2^{cp}}$ . However,

$$ \begin{align*}\bigcup_{f_\unicode{x3bb}\text{ is not critically periodic}}(R_\unicode{x3bb}\cup S^1)\times \{\unicode{x3bb}\}\end{align*} $$

is dense in R, and hence $R\subset {\Upsilon _2^{cp}}$ .

8 Algorithms to test membership of ${\Xi }_\unicode{x3bb} $

In this section, we will describe an algorithm to check if a point $z_0\in \mathbb {C}$ is in the complement of a slice ${\Xi }_\unicode{x3bb} $ for $\unicode{x3bb} \in (1, 2)$ .

First, if $\unicode{x3bb} <\sqrt {2}$ , Theorems 1.7 and 1.8 imply that $z\in {\Xi }_\unicode{x3bb} $ if and only if $z^2\in {\Xi }_{\unicode{x3bb} ^2}$ , so we can always reduce the question to the case $\unicode{x3bb} \in [\sqrt {2}, 2)$ .

8.1 Testing $z_0$ with $|z_0|> 1$

When $|z_0|>1$ , Theorem 1.8 gives us a straightforward way to test if $z_0\not \in {\Xi }_\unicode{x3bb} $ : calculating the first few terms of the power series $H(\mathrm {{It}}_\unicode{x3bb} , z^{-1})$ , then checking if $z_0^{-1}$ is a root of this power series. More precisely, we have the following algorithm.

Algorithm 1.

Remark 8.1. If instead of checking if $z_0\not \in {\Xi }_\unicode{x3bb} $ , we want to see if an $\epsilon $ -neighborhood of $z_0$ is contained in the complement of ${\Xi }_\unicode{x3bb} $ , we can change the last line of Algorithm 1 to make use of Rouché’s theorem.

8.2 Testing $z_0$ with $|z_0| < 1$

If $|z_0|<1$ , a way to certify that $z_0\not \in {\Xi }_\unicode{x3bb} $ is by first finding the set of all words of length N that satisfy conditions (1)–(3) of Definition 1.5 (condition (4) is trivial because $\unicode{x3bb} \geq \sqrt {2}$ ), denoted as $\mathcal {M}_{N, \unicode{x3bb} }$ , for each word $w=(w_1\ldots w_N)\in \mathcal {M}_{N, \unicode{x3bb} }$ , evaluating $f_{w_N, z_0}^{-1}\circ f_{w_{N-1}, z_0}^{-1}\ldots f_{w_1, z_0}^{-1}(1)$ , and checking that they are all sufficiently large. More precisely, the algorithm can be described as follows.

Algorithm 2.

Remark 8.2. In the definition of $\mathcal {M}_{N, \unicode{x3bb} }$ above, one needs to check conditions (1)–(3) in Definition 1.5 for all the $\unicode{x3bb} '>\unicode{x3bb} $ . However, in practice, one does not really need to check these conditions for infinitely many $\unicode{x3bb} '$ : instead, one can pick a decreasing sequence $\unicode{x3bb} ^{\prime }_j$ converging to $\unicode{x3bb} $ , then there must be some $j=j_0$ such that for any $i\leq N$ , let $f_s$ be the s-tent map, then $H_i(s)=f_s^{\circ i}(1)$ does not have any critical points in $(\unicode{x3bb} , \unicode{x3bb} ^{\prime }_{j_0})$ . One can show that the N-prefix of $\mathrm {{It}}_{\unicode{x3bb} ^{\prime }_j}$ for $j>j_0$ should be the same as the N-prefix of $\mathrm {{It}}_{\unicode{x3bb} ^{\prime }_{j_0}}$ , and in Definition 1.5, the only thing we ever used for $\mathrm {{It}}_{\unicode{x3bb} '}$ is its N-prefix, so we can set $\unicode{x3bb} '=\unicode{x3bb} ^{\prime }_{j_0}$ and verify the three conditions in finite time.

The reason that Algorithm 2 is true is due to the following proposition.

Proposition 8.3. Let $\unicode{x3bb} \in [\sqrt {2}, 2)$ , and let $\mathcal {M}_{N, \unicode{x3bb} }$ be defined as in Algorithm 2. Suppose $|z|<1$ , then $z\not \in {\Xi }_\unicode{x3bb} $ if and only if there exists $N \in \mathbb {N}$ such that for every word $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$ ,

$$ \begin{align*}f_{w_N, z}^{-1}\circ \cdots \circ f_{w_1, z}^{-1}(1)\geq {2\over 1-|z|}+\epsilon.\end{align*} $$

Proof. First, we assume that there is some N such that for every word $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$ ,

$$ \begin{align*}f_{w_N, z}^{-1}\circ \cdots \circ f_{w_1, z}^{-1}(1)\geq {2\over 1-|z|}+\epsilon\end{align*} $$

and prove that $z\not \in {\Xi }_\unicode{x3bb} $ . Suppose $z\in {\Xi }_\unicode{x3bb} $ . Then by Theorem 1.7, there must be some $\unicode{x3bb} $ -suitable sequence $v=v_1v_2\ldots $ such that

$$ \begin{align*}1=G(v, z)=\lim_{n\rightarrow\infty}f_{v_1, z} \circ\cdots \circ f_{v_n, z}(1).\end{align*} $$

In other words, for any $\delta>0$ , there is some $n>N$ such that

$$ \begin{align*} |f_{v_1, z}\circ\cdots \circ f_{v_n, z}(1)-1 |<\delta.\end{align*} $$

By the definition of $\mathcal {M}_{N, \unicode{x3bb} }$ , the word $v_1\ldots v_N\in \mathcal {M}_N$ . Let $u=f_{v_1, z}\circ \cdots \circ f_{v_n, z}(1)$ . Then, $|u-1|<\delta $ . Because $f_{v_N, z}^{-1} \circ \cdots \circ f_{v_1, z}^{-1}$ is continuous, we can pick $\delta $ small enough such that

$$ \begin{align*}f_{v_N, z}^{-1}\circ \cdots \circ f_{v_1, z}^{-1}(u)>{2\over 1-|z|}.\end{align*} $$

However,

$$ \begin{align*}f_{v_N, z}^{-1}\circ \cdots \circ f_{v_1, z}^{-1}(u)=f_{v_{N+1}, z}\circ\cdots \circ f_{v_n, z}(1).\end{align*} $$

By calculation, it is easy to verify that $1$ is in the disc

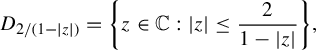$$ \begin{align*}D_{2/ ({1-|z|})}= \bigg\{z\in\mathbb{C}:|z|\leq {2\over {1-|z|}} \bigg\},\end{align*} $$

and both $f_{0, z}$ and $f_{1, z}$ send $D_{2/ ({1-|z|})}$ to itself. Hence,

$$ \begin{align*} |f_{v_{N+1}, z}\circ\cdots \circ f_{v_n, z}(1) |\leq {2\over {1-|z|}},\end{align*} $$

which is a contradiction.

Now, for the other direction, we assume that for any $N \in \mathbb {N}$ , there is some word $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$ such that

$$ \begin{align*}f_{w_N, z}^{-1}\circ \cdots \circ f_{w_1, z}^{-1}(1)\leq {2\over 1-|z|}\end{align*} $$

and prove that $z\not \in {\Xi }_\unicode{x3bb} $ . Let $C_N$ be the set of sequences such that an N-prefix of it is in $\mathcal {M}_{N, \unicode{x3bb} }$ , and this N prefix is of the form $w_1\ldots w_N$ such that

$$ \begin{align*}f_{w_N, z}^{-1}\circ f_{w_{N-1}, z}^{-1}\ldots f_{w_1, z}^{-1}(1)\leq {2\over 1-|z|}.\end{align*} $$

The fact that $f_{0, z}$ and $f_{1, z}$ both send $D_{2/({1-|z|})}$ to itself implies that $C_{N+1}\subset C_{N}$ , and all these sets are non-empty and compact under the product topology, and hence their intersection is non-empty. Let $w\in \bigcap _NC_N$ , then w is $\unicode{x3bb} $ -suitable and it is easy to see that $G(w, z)=1$ .

Furthermore, we have an effective version of the Proposition 8.3 above.

Proposition 8.4. Let $\unicode{x3bb} $ , z, N, and $\epsilon $ be as in Proposition 8.3 above, ${1\over 2}<|z|<1$ . Then for any $y\in \mathbb {C}$ , if

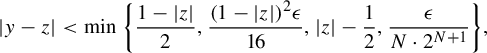$$ \begin{align*}|y-z|<\min \bigg\{{1-|z|\over 2}, {(1-|z|)^2\epsilon\over 16}, |z|-{1\over 2}, {\epsilon\over N\cdot 2^{N+1}} \bigg\},\end{align*} $$

then $y\not \in {\Xi }_\unicode{x3bb} $ .

Remark 8.5. The assumption $|z|>{1\over 2}$ is a reasonable one because it is well known (cf. [Tio18]) that if $|z|<{1\over 2}$ , then $z\not \in {\Xi }_\unicode{x3bb} $ for any $\unicode{x3bb} \in (1, 2)$ .

Proof. It is easy to see that as long as $|y|<1$ ,

$$ \begin{align*}\bigg|{2\over 1-|z|}-{2\over 1-|y|}\bigg|<\epsilon/2,\end{align*} $$

and for any $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$ ,

$$ \begin{align*} |f_{w_N, z}^{-1}\circ f_{w_{N-1}, z}^{-1}\ldots f_{w_1, z}^{-1}(1)-f_{w_N, y}^{-1}\circ f_{w_{N-1}, y}^{-1}\ldots f_{w_1, y}^{-1}(1)|<\epsilon/2,\end{align*} $$

then y also satisfies the assumption in Proposition 8.3. The first condition, $|y|<1$ , holds because $|y-z|<{(1-|z|)/ 2}$ , which implies $|y|<{(1+|z|)/ 2}<1$ . The second condition,

$$ \begin{align*}\bigg|{2\over 1-|z|}-{2\over 1-|y|}\bigg|<\epsilon/2,\end{align*} $$

holds because $|y|<{(1+|z|)/ 2}$ and $|y-z|<{(1-|z|)^2\epsilon / 16}$ . The third condition,

$$ \begin{align*} |f_{w_N, z}^{-1}\circ f_{w_{N-1}, z}^{-1}\ldots f_{w_1, z}^{-1}(1)-f_{w_N, y}^{-1}\circ f_{w_{N-1}, y}^{-1}\ldots f_{w_1, y}^{-1}(1) |<\epsilon/2,\end{align*} $$

holds because of the following argument. As a polynomial of ${1/ z}$ ,

$$ \begin{align*}f_{w_N, z}^{-1}\circ f_{w_{N-1}, z}^{-1}\ldots f_{w_1, z}^{-1}(1)\end{align*} $$

has degree N and coefficients bounded between $-2$ and $2$ , and hence has its derivative bounded by $N2^{N-1}\cdot 2=N\cdot 2^N$ on the annulus $\{y\in \mathbb {C}:1\leq |y|\leq 2\}$ . Because $|y-z|<|z|-{1\over 2}$ , y is inside this annulus, so this third condition follows from the assumption that $|y-z|<{\epsilon / N\cdot 2^{N+1}}$ and the mean value theorem.

9 Asymmetry of ${\Xi }_{\unicode{x3bb} }$

The following proposition is likely well known to experts; we include the proof for completeness.

Proposition 9.1. $\Omega _2^{cp} \cap \mathbb {D}$ is invariant under reflection across the real axis and across the imaginary axis.

Proof. The set $\Omega _2^{cp} \cap \mathbb {D}$ is invariant under reflection across the real axis because Galois conjugates come in complex conjugate pairs. Tiozzo [Tio18] showed that $\Omega _2^{cp} \cap \mathbb {D}\backslash S^1$ is the set of all the roots in $\mathbb {D}$ of all power series with all coefficients in $\{\pm 1\}$ . So if $z \in \mathbb {D}$ is a root of a power series S with coefficients in $\{\pm 1\}$ , then $-z$ is a root of the power series formed from S by flipping the sign of the coefficients on all terms of odd degree. Therefore, the complex conjugate, $\overline {-z}$ , is in $\Omega _2^{cp}$ .

However, our Algorithm 2 in the previous section can be used to show that ${\Xi }_\unicode{x3bb} \cap \mathbb {D}$ does not necessarily have such symmetry, which proves Theorem 1.14.

Proof of Theorem 1.14

We only need to show that there is some $z\in {\Xi }_{1.82}\cap \mathbb {D}$ such that $-z\not \in {\Xi }_{1.82}\cap \mathbb {D}$ . Consider the tent map with growth rate being the leading root of

$$ \begin{align*}-1 + z^2 - z^4 + z^6 - 2 z^7 + 3 z^8 - 4 z^9 + 3 z^{10} - 2 z^{11} + z^{12} - 2 z^{13} + z^{14},\end{align*} $$

which is approximately $1.8149185987640513$ and is smaller than $1.82$ , and hence any Galois conjugate of this leading root must be in ${\Xi }_{1.82}$ . Let z be the Galois conjugate near the point $-0.5840341196392905+0.4820600149798202 i$ . Applying Algorithm 2 to $-z$ for $N=20$ shows that $-z\not \in {\Xi }_{1.82}$ .