Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T13:03:36.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of regular dicritical foliations

Published online by Cambridge University Press:  23 March 2016

GABRIEL CALSAMIGLIA  and
YOHANN GENZMER
GABRIEL CALSAMIGLIA
Affiliation:
Instituto de Matemática, Universidade Federal Fluminense, Rua Mário Santos Braga s/n, 24020-140, Niterói, Brazil email gabriel@mat.uff.br
YOHANN GENZMER
Affiliation:
I.M.T., Université Paul Sabatier, Toulouse, France email yohann.genzmer@math.univ-toulouse.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we give complete analytic invariants for the set of germs of holomorphic foliations in 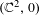$(\mathbb{C}^{2},0)$ that become regular after a single blow-up. Some of the invariants describe the holonomy pseudogroup of the germ and are called transverse invariants. The other invariants lie in a finite dimensional complex vector space. Such singularities admit separatrices tangentially to any direction at the origin. When enough separatrices are leaves of a radial foliaton (a condition that can always be attained if the multiplicity of the germ at the origin is at most four) we are able to describe and realize all the analytical invariants geometrically and provide analytic normal forms. As a consequence, we prove that any two such germs sharing the same transverse invariants are conjugated by a very particular type of birational transformation. We also provide explicit examples of universal equisingular unfoldings of foliations that cannot be produced by unfolding functions. With these at hand we are able to explicitly parametrize families of analytically distinct foliations that share the same transverse invariants.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 5 , August 2017 , pp. 1443 - 1479
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, M.. On the solutions of analytic equations. Invent. Math. 5 (1968), 277–291.CrossRefGoogle Scholar
Brunella, M.. Birational Theory of Foliations (IMPA Monographs, 1). Springer, New York, 2015.Google Scholar
Calsamiglia, G.. Finite determinacy of dicritical singularities. Ann. Inst. Fourier (Grenoble) 57(2) (2007), 673–691.CrossRefGoogle Scholar
Camacho, C. and Movasati, H.. Neighborhoods of Analytic Varieties (Monografias del IMCA, MI-35). IMCA, Lima, 2003.Google Scholar
Camacho, C. and Sad, P.. Invariant varieties through singularities of vector fields. Ann. of Math. (2) 115 (1982), 579–595.Google Scholar
Genzmer, Y.. Analytical and formal classification of quasi-homogeneous foliations. J. Differential Equation 245(6) (2008), 1656–1680.Google Scholar
Genzmer, Y. and Paul, E.. Normal forms of foliations and curves defined by a function with generic tangent cone. Mosc. Math. J. (1) (2011), 41–72.Google Scholar
Ilyashenko, Yu. S.. Topology of phase portraits of analytic differential equations on a complex projective plane. Tr. Semin. im. I. G. Petrovskogo 4 (1978), 83–136.Google Scholar
Klughertz, M.. Existence d’une intégrale première méromorphe pour des germes de feuilletages à feuilles fermées du plan complexe. Topology 2 (1992), 255–269.Google Scholar
Loray, F.. A preparation theorem for codimension-one foliations. Ann. of Math (2) 2 (2006), 709–722.Google Scholar
Marin, D.. Moduli spaces of germs of holomorphic foliations in the plane. Comment. Math. Helv. 78(3) (2003), 518–539.Google Scholar
Mattei, J.-F.. Modules de feuilletages holomorphes singuliers. I. Équisingularité. Invent. Math. 103(2) (1991), 297–325.Google Scholar
Mattei, J.-F. and Salem, E.. Modules formels locaux de feuilletages holomorphes. Preprint, 2010.Google Scholar
Ortiz, L., Rosales, E. and Voronin, S.. Rigidity theorems for generic holomorphic germs of dicritic foliations and vector fields in (ℂ2, 0). Mosc. Math. J. 5(1) (2005), 171–206.Google Scholar
Ortiz, L., Rosales, E. and Voronin, S.. Analytic normal forms of germs of holomorphic dicritic foliations. Mosc. Math. J. 8(3) (2008), 521–545, 616.Google Scholar
Ortiz, L., Rosales, E. and Voronin, S.. Thom’s problem for degenerated singular points of holomorphic foliations in the plane. Mosc. Math. J. 12(4) (2012), 825–862.Google Scholar
Perez-Marco, R.. Sur les dynamiques holomorphes non-linéarisables et une conjecture de V.I. Arnold. Ann. Sci. Éc. Norm. Supér. (4) 26(5) (1993), 565–644.Google Scholar
Savelev, V. I.. Zero-type embedding of a sphere into complex surfaces. Moscow Univ. Math. Bull. 37 (1982), 34–39.Google Scholar
Ueda, T.. On the neighborhood of a compact complex curve with topologically trivial normal bundle. Kyoto J. Math. Univ. 22(4) (1982/83), 583–607.Google Scholar