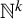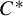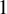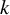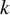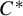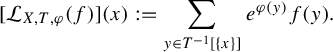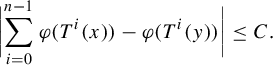Cocycles on groupoids arising from $\mathbb {N}^k$-actions

Abstract

We consider groupoids constructed from a finite number of commuting local homeomorphisms acting on a compact metric space and study generalized Ruelle operators and $ C^{\ast } $ -algebras associated to these groupoids. We provide a new characterization of $ 1 $ -cocycles on these groupoids taking values in a locally compact abelian group, given in terms of $ k $ -tuples of continuous functions on the unit space satisfying certain canonical identities. Using this, we develop an extended Ruelle–Perron–Frobenius theory for dynamical systems of several commuting operators ( $ k $ -Ruelle triples and commuting Ruelle operators). Results on KMS states on $ C^{\ast } $ -algebras constructed from these groupoids are derived. When the groupoids being studied come from higher-rank graphs, our results recover existence and uniqueness results for KMS states associated to the graphs.

1 Introduction

Let X be a compact Hausdorff space and $ \sigma : X \to X $ a local homeomorphism of $ X $ onto itself. The so-called Deaconu–Renault groupoid and its associated $C^*$ -algebra corresponding to the pair $ ({X,\sigma }) $ were first studied by Deaconu in [7] based on a construction of Renault in [22] in the setting of groupoids of Cuntz algebras. Deaconu adapted Renault’s construction by replacing the shift map on the infinite sequence space with a local homeomorphism. Renault further generalized this construction to local homeomorphisms defined on open subsets in [23]. The étale groupoid associated to a finite family of commuting local homeomorphisms of a compact metric space has gone by various names including Deaconu–Renault groupoids of higher rank and the semidirect product groupoid corresponding to the action of the semigroup $ \mathbb {N}^{k} $ [10]. In [26], these groupoids were generalized to the setting of partial semigroup actions. Our main purpose in this paper is the study of these groupoids, their associated $ C^{\ast } $ -algebras, and KMS states which arise naturally on a specific class of related dynamical systems. This is a sufficiently broad class to include higher-rank graph $C^*$ -algebras associated to finite k-graphs. We develop cohomological methods to characterize $ 1 $ -cocycles on these $ C^{\ast } $ -algebras, which in turn give rise to one-parameter automorphism groups. This leads us to study the KMS states on these $ C^{\ast } $ -algebras.

KMS states have their origin in equilibrium statistical mechanics and have long been a very fruitful tool in the study of operator algebras. For the precise definition of KMS states see [12] and the references contained therein. In this paper, we study KMS states for groupoids associated to a finite family of commuting local homeomorphisms of a compact metric space by further developing a Ruelle–Perron–Frobenius (RPF) theory of dynamical systems of several commuting operators. Although an RPF theory for free abelian semigroups has been introduced by Carvalho, Rodrigues, and Varandas in [4, 5], their main emphasis was on skew products, random walks, and topological entropy, whereas our emphasis here will be on the connection to the $ C^{\ast } $ -algebras and the use of the Ruelle–Perron–Frobenius operator to prove the existence of measures with appropriate properties (hence states with related properties).

In the groupoid perspective, as first explained by Renault in [22], time evolutions (dynamics) on the reduced $ C^{\ast } $ -algebra of a groupoid $ \mathcal {G} $ are implemented by continuous real-valued $ 1 $ -cocycles on $ \mathcal {G} $ and the task of understanding the KMS states for these dynamics on $ C^{\ast }_{\textrm {r}} ({\mathcal {G}}) $ requires, at a minimum, identifying the measures on the unit space of $ \mathcal {G} $ that are quasi-invariant. There are now refinements of Renault’s result; see, for example, work by Neshveyev [20] and Thomsen [30]. More recently, Christensen’s paper [6] combines quasi-invariant measures with a certain group of symmetries to describe KMS states on groupoid $ C^{\ast } $ -algebras for locally compact second countable Hausdorff étale groupoids.

Our analysis of the KMS states on groupoids associated to a finite family of commuting local homeomorphisms of a compact metric space stems from a new characterization of their continuous real-valued $1$ -cocycles, which in a nutshell are determined completely by a $ k $ -tuple of continuous real-valued functions on the unit space of the groupoid satisfying canonical identities. In so doing, we give an isomorphism between the first monoid cohomology of $ \mathbb {N}^{k} $ with coefficients in the module $ \operatorname {C} ({X,H}) $ of continuous functions on X with values in H, where $ H $ is a locally compact abelian group, and the first continuous cocycle groupoid cohomology taking values in $ H $ .

We base our constructions on the established analysis of KMS states on Deaconu–Renault groupoids of [9, 13, 17, 24], together with an extended Ruelle–Perron–Frobenius theory for dynamical systems of several commuting operators, modelled on the one-dimensional theory of Ruelle [27] and Walters [31].

In [17], Kumjian and Renault associated KMS states to Ruelle operators constructed on a groupoid arising from a single expansive map and, in [13], Ionescu and Kumjian related the associated states to Hausdorff measures, which led to applications to KMS states on Cuntz algebras, $ C^{\ast } $ -algebras arising from directed graphs, and $ C^{\ast } $ -algebras associated to fractafolds. In addition, Ruelle operators were used in [2]. In this paper, we generalize some of these results to groupoids associated to a finite family of commuting local homeomorphisms of a compact metric space. In particular, we deduce that in order for the adjoint of the Ruelle operator associated to a finite family of commuting local homeomorphism to have an eigenmeasure, it is necessary and sufficient that the adjoint of the Ruelle operator corresponding to a non-trivial product of the local homeomorphisms have that same eigenmeasure, thus reducing matters to the one-dimensional case studied by Walters.

Ruelle operators are important tools in mathematical physics, particularly thermodynamics, and yield a formulation of a ‘continuous’ extension of the seminal Perron–Frobenius theorem. Ruelle’s classical result, known as the ‘Ruelle–Perron–Frobenius (RPF) theorem’, gives a sufficient condition for a Ruelle triple to satisfy the unique positive eigenvalue condition [27, 28]. In [32], building on earlier work of Bowen, Walters gave criteria for the RPF theorem to hold for more general Ruelle triples $ ({X,\sigma ,\varphi }) $ merely demanding that $ X $ be a metric space, $ \sigma $ be positively expansive and exact, and $ \varphi $ satisfy a smoothness condition. We extend the RPF theorem to certain Ruelle triples of type $ ({X,\sigma ,\varphi }) := ({X,\sigma _{i},\varphi _{i}})_{i = 1}^{k} $ , where the $ \sigma _{i} $ form a commuting family of local homeomorphisms which are positively expansive and exact, and the $ \varphi _{i} $ satisfy the Walters conditions.

To derive our generalization of the the RPF theorem, we first need to construct continuous $ 1 $ -cocycles on the groupoid $ \mathcal {G} ({X,\sigma }) $ arising from a $ k $ -tuple of commuting local homeomorphisms on $ X $ with values in $ \mathbb {R} $ . In order to study this in the greatest possible generality, we first study the problem of calculating $ H^{1} ({\mathbb {N}^{k},A}) $ , where $ A $ is an $ \mathbb {N}^{k} $ -module. In Theorem 3.4, we are able to give an explicit formula for all elements of $ Z^{1} ({\mathbb {N}^{k},A}) $ from $ k $ -tuples in $ A^{k} $ satisfying what we call the ‘module cocycle condition’ and describe which of these are coboundaries. In the case $ k = 1 $ , this formula is similar to the formula given in [8].

We apply this theorem by starting with a $ k $ -tuple of commuting local homeomorphisms of $ X $ and using them to give $ \operatorname {C} ({X,H}) $ an $ \mathbb {N}^{k} $ -module structure for any locally compact abelian group $ H $ . We then provide an explicit isomorphism between $ H^{1} ({\mathbb {N}^{k},\operatorname {C} ({X,H})}) $ and the first cohomology group $ H_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ of the groupoid $ \mathcal {G} ({X,\sigma }) $ . Specializing to the case where $ H = \mathbb {R} $ , we obtain explicit formulas for elements of $ Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),\mathbb {R}}) $ that we use in the generalized RPF theorem.

Recently there has been great interest (cf. [1, 12, 18]) in the KMS states associated to one-parameter dynamical systems on $ C^{\ast } ({\Lambda }) $ , where $ \Lambda $ is a higher-rank graph and the dynamics arises either from the canonical gauge action of $ \mathbb {T}^{k} $ on $ C^{\ast } ({\Lambda }) $ or from a generalized gauge action. In particular, for a finite strongly connected $ k $ -graph, in [1, 12, 18], one can endow $ C^{\ast } ({\Lambda }) $ with a (generalized) gauge dynamics and show the existence of unique KMS states. Here, we are able to recover some of the results in [1, 12, 18] from a different perspective, using the Ruelle–Perron–Frobenius theorem and the generalized gauge dynamics that we obtain from our description of $ Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),\mathbb {R}}) $ given in Proposition 3.10.

We now outline the structure of the paper. Section 2 introduces classical Ruelle triples, triples that satisfy the unique positive eigenvalue condition (see Definition 2.3), and Ruelle operators. These are basic objects that we will generalize to higher dimensions in §4. We also review several essential results of Walters, Bowen, and Ruelle in this section. In §3, we review the construction of the groupoid $\mathcal {G} ({X,\sigma })$ associated to a finite family $\sigma $ of commuting local homeomorphisms of a compact metric space X, and then briefly review level-one semigroup cohomology and continuous groupoid cohomology and relate the two. We also give an algebraic way of constructing all continuous $ 1 $ -cocycles in both the semigroup and groupoid cases. Our main interest are continuous real-valued $ 1 $ -cocycles on $ \mathcal {G} ({X,\sigma }) $ . In §4, we introduce $ k $ -Ruelle dynamical systems, the related families of commuting Ruelle operators and their duals, and their eigenmeasures. In §5, we use the results of the previous sections to consider the Radon–Nikodym problem for these groupoids, which provides a link between quasi-invariant measures for the groupoids $\mathcal {G} ({X,\sigma })$ and KMS states for a generalized gauge dynamics. In particular, we prove that if the generalized Ruelle operator associated to a k-Ruelle system has an eigenmeasure with eigenvalue one, then there exists a KMS state for the generalized gauge dynamics coming from certain groupoid $ 1 $ -cocycles related to the groupoid $ C^{\ast } $ -algebra. Finally, in §6, we apply the results obtained thus far to answer some existence and uniqueness questions concerning KMS states for a generalized gauge dynamics associated to higher-rank graphs.

1.1 Notation and conventions

In the rest of the paper, we will use the following notational conventions. We denote by $ \mathbb {N} $ the semigroup of natural integers $ \{ 0,1,2,\ldots \} $ and by $ \mathbb {N}_{>0} $ the set of positive elements of $\mathbb {N}$ . For fixed $ k \in \mathbb {N}_{>0} $ , we denote by $\mathbb {N}^k$ the semigroup of all ordered k-tuples of elements of $\mathbb {N}$ and by $ [ k ] $ the set $[ k ]=\{ 1,\ldots ,k \} $ . We define the length $\lvert n \rvert $ of an element $n=(n_1,\ldots, n_k) \in \mathbb {N}^k$ by $\lvert n \rvert := n_{1} + \cdots + n_{k} $ .

For every compact Hausdorff space $ X $ , and topological locally compact group H, we let $ C(X,H) $ be the group of continuous functions from X to H. In many instances $H=\mathbb {R} $ in this paper. We will also let $ \mathcal {M} ({X}) $ denote the Banach space of finite signed Borel measures on the Borel subsets of $ X $ , which is isometrically isomorphic to the dual space $ C(X,\mathbb {R})' $ of $ C(X,\mathbb {R}) $ .^†

For every (locally) compact Hausdorff étale groupoid $ \mathcal {G} $ , there is a standard dense linear embedding of $ \operatorname {C_{c}} ({\mathcal {G}}) $ into $ C^{\ast }_{\textrm {r}} ({\mathcal {G}}) $ . The groupoids that we study are amenable, so, unless there is a danger of confusion, we shall identify $ f \in \operatorname {C_{c}} ({\mathcal {G}}) $ with its image (also denoted by $ f $ ) in $ C^{\ast }_{\textrm {r}} ({\mathcal {G}}) \cong C^{\ast } ({\mathcal {G}}) $ .

In what follows, $ X $ will always denote a (non-empty) compact Hausdorff topological space.

2 Ruelle triples and Ruelle operators

We begin by defining Ruelle triples and Ruelle operators (sometimes called transfer operators), which were introduced in [27] in the case of totally disconnected spaces and generalized to arbitrary compact metric spaces by Walters in [31, 32]. These will be the basic objects of concern in this paper. Ruelle operators are important tools in mathematical physics, particularly thermodynamics, and yield a formulation of a ‘continuous’ extension of the classical Perron–Frobenius theorem. In [17], Kumjian and Renault associated KMS states to Ruelle operators constructed on a groupoid arising from a single expansive map on a compact metric space, which led to applications to KMS states on Cuntz $ C^{\ast } $ -algebras and $ C^{\ast } $ -algebras associated to higher-rank graphs.

Definition 2.1. (Ruelle triples and operators)

1. (1) A Ruelle triple is an ordered triple $ ({X,T,\varphi }) ,$ where:

   1. (a) $ X $ is a compact metric space;

   2. (b) $ T : X \to X $ is a surjective local homeomorphism;

   3. (c) $ \varphi : X \to \mathbb {R} $ is a continuous function, that is, $ \varphi \in \operatorname {C} ({X,\mathbb {R}}) $ .

2. (2) The Ruelle operator associated to a Ruelle triple $ ({X,T,\varphi }) $ is the bounded linear operator

   $$ \begin{align*}\mathcal{L}_{X,T,\varphi}: \operatorname{C} ({X,\mathbb{R}}) \to \operatorname{C} ({X,\mathbb{R}}) \end{align*} $$
   defined by, for all $f \in \operatorname {C} ({X,\mathbb {R}}), ~ \text { for all } x \in X$ ,
   (1) $$ \begin{align} [ \mathcal{L}_{X,T,\varphi} ({f}) ] ({x}) := \sum_{y \in T^{- 1} [ \{ x \} ]} e^{\varphi ({y})} f ({y}). \end{align} $$

Our goal is to extend some results from [13, 17, 25] from a single local homeomorphism to commuting k-tuples of local homeomorphisms on $ X $ in part by employing cohomological methods. The following lemma follows from [10, Proposition 2.2].

Lemma 2.2. (Composition of Ruelle operators)

Let $ ({X,S,\varphi }) $ and $ ({X,T,\psi }) $ be Ruelle triples. Then $ ({X,S \circ T,\varphi \circ T + \psi }) $ is a Ruelle triple and

$$ \begin{align*}\mathcal{L}_{X,S,\varphi} \circ \mathcal{L}_{X,T,\psi} = \mathcal{L}_{X,S \circ T,\varphi \circ h + \psi}. \end{align*} $$

We will now define an important subclass of Ruelle triples, those for which the positive eigenvalue problem for the dual Ruelle operator has a unique solution. These Ruelle triples enjoy important fixed-point properties and admit generalizations to dynamical systems that will be described in §4.

Definition 2.3. A Ruelle triple $ ({X,T,\varphi }) $ is said to satisfy the unique positive eigenvalue condition if there exists a unique ordered pair $ ({\unicode{x3bb} ,\mu }) $ such that:

1. (1) $ \unicode{x3bb} $ is a positive real number;

2. (2) $ \mu $ is a Borel probability measure on $ X $ ;

3. (3) if we denote by $ ({\mathcal {L}_{X,T,\varphi }})^{\ast }: \mathcal {M} ({X}) \to \mathcal {M} ({X}) $ the dual of the Ruelle operator $ \mathcal {L}_{X,T,\varphi } $ , then

   $$ \begin{align*} ({\mathcal{L}_{X,T,\varphi}})^{\ast} ({\mu}) = \unicode{x3bb} \mu .\end{align*} $$

Ruelle’s classical result, known as the ‘Ruelle–Perron–Frobenius (RPF) theorem’, generalizes the seminal Perron–Frobenius theorem for primitive matrices to subshifts of finite type and gives a sufficient condition for a Ruelle triple to satisfy Definition 2.3 [27, 28]. The RPF theorem below is taken from [9, Theorem 2.2].

To introduce the required notation to state the RPF theorem, fixing $ k \in \mathbb {N}_{> 0} $ , let $ A = ({A_{i,j}})_{i,j \in [ k ]}$ be an $ {n \times n} $ zero–one matrix with no row or column of zeros and let $ ({\Sigma _{A},\sigma }) $ be the associated (one-sided) subshift of finite type, where $ \Sigma _{A} $ is the compact topological subspace of the infinite product space $ \prod _{j \in \mathbb {N}} [ k ] $ defined by

$$ \begin{align*}\Sigma_{A} := \bigg\{{x = ({x_{0},x_{1},x_{2},\ldots}) \in \prod_{j \in \mathbb{N}} [ k ]}~ \bigg|~{A_{x_{i},x_{i + 1}} = 1\quad\text{for all } i \geq 0}\bigg\} \end{align*} $$

and $ \sigma : \Sigma _{A} \to \Sigma _{A} $ is the ‘left shift’ given by

$$ \begin{align*}\sigma ({x_{0},x_{1},x_{2},\ldots}) = ({x_{1},x_{2},x_{3},\ldots}). \end{align*} $$

Moreover, given a real number $ \beta \in ({0,1}) $ , we define a compatible metric $ d $ on $ \Sigma _{A} $ by setting, for $ x,y \in \Sigma _{A} $ and $ x \neq y $ , $ d ({x,y}) = \beta ^{N ({x,y})} $ , where $ N ({x,y}) $ is the least integer $ N \in \mathbb {N} $ such that $ x_{i} \not = y_{i} $ . Furthermore, $ \min ({\varnothing }) := \infty $ by convention; in this case $d(x,y)=0$ .

We can now state the Ruelle–Perron–Frobenius theorem as presented by Exel; see [9, Theorem 2.2] and [9, Proposition 2.3].

Theorem 2.4. (Ruelle–Perron–Frobenius theorem)

With notation as above, let $ \varphi $ be a continuous real-valued function defined on $ \Sigma _{A} $ . Suppose that:

1. (1) there exists a positive integer $ m $ such that $ A^{m}> 0 $ (in the sense that all entries are positive); and

2. (2) $ \varphi $ is Hölder-continuous.

Then there exist a strictly positive function $ h \in \operatorname {C} ({\Sigma _{A},\mathbb {R}}) $ , a Borel probability measure $ \mu $ on $ \Sigma _{A} $ , and a positive real number $ \unicode{x3bb} $ such that:

1. (a) $ ({\mathcal {L}_{\Sigma _A,\sigma ,\varphi }}) ({h}) = \unicode{x3bb} h $ ; and

2. (b) $ ({\mathcal {L}_{\Sigma _A,\sigma ,\varphi }})^{\ast } ({\mu }) = \unicode{x3bb} \mu $ .

In particular, $ ({\Sigma _A,\sigma ,\varphi }) $ also satisfies the unique positive eigenvalue condition of Definition 2.3.

In the following, we will also refer to the Ruelle–Perron–Frobenius theorem as the RPF theorem. In [32, 33], Walters gave criteria for the RPF theorem to hold for more general Ruelle triples $ ({X,T,\varphi }) $ , which was modified by Kumjian and Renault in [17], requiring that $ X $ be a metric space, $ T $ be positively expansive and exact, and $ \varphi $ obey some summability condition. We will now detail these results.

Definition 2.5. Let $ ({X,T,\varphi }) $ be a Ruelle triple and let $ d $ be the metric on $ X $ . Consider the three conditions listed below.

1. (1) $ T $ is positively expansive, that is, there is an $ \epsilon> 0 $ such that for all distinct $ x,y \in X $ , there exists an $ n \in \mathbb {N} $ such that $ d ({T^{n} ({x}),T^{n} ({y})}) \geq \epsilon $ .

2. (2) $ T $ is exact, that is, for every non-empty open subset $ U $ of $ X $ , there exists an $ n \in \mathbb {N} $ such that $ T^{n} [ U ] = X $ .

3. (3) There exist a compatible metric $ d' $ on $ X $ and positive numbers $ \delta> 0 $ and $ C> 0 $ with the property that for all $n \in \mathbb {N}_{> 0} $ and for all $ x,y \in X $ , we have that $ d' ({T^{i} ({x}),{T}^{i} ({y})}) \leq \delta $ for all $ i \in \{ 0,1,\ldots ,n - 1 \} $ implies that

   $$ \begin{align*}\bigg\lvert{\sum_{i = 0}^{n - 1} \varphi ({T^{i} ({x})}) - \varphi ({T^{i} ({y})})}\bigg\rvert \leq C. \end{align*} $$

We say that $ (X, T,\varphi )$ satisfies the Walters conditions if it satisfies Conditions (1) and (2) above, and it satisfies the Bowen condition [3] if it satisfies Condition (3) above. Moreover, $ T $ is positively expansive if and only if there is an open neighbourhood $ U $ of $ \Delta ({X}) $ , the diagonal of $ X $ , such that for all distinct $ x,y \in X $ , there exists an $ n \in \mathbb {N} $ such that $ ({T^{n} ({x}),T^{n} ({y})}) \notin U $ .

In all of our examples the function $\varphi $ is Hölder continuous, and that together with Condition (1) implies the Bowen condition, as noted in the following well-known proposition, whose proof is sketched in [17, p. 2071].

Proposition 2.6. Let $ ({X,T,\varphi }) $ be a Ruelle triple with T positively expansive. If $ \varphi $ is Hölder-continuous with respect to a compatible metric $ d $ on $ X $ , then Condition (3) of Definition 2.5 is satisfied for $ d $ by $ \varphi $ with respect to $ T $ .

The main results of [14, 32] yield the following theorem.

Theorem 2.7. A Ruelle triple satisfies the unique positive eigenvalue condition of Definition 2.3 if it satisfies the conditions in Definition 2.5.

In [14], Jiang and Ye stated analogous conditions for weakly contractive iterated function systems for which results similar to Theorem 2.7 hold.

3 Continuous $ 1 $ -cocycles on semigroups and continuous $ 1 $ -cocycles on $ \mathcal {G} ({X,\sigma }) $

3.1 Semigroup cocycles

We now discuss semigroup cocycles with values in a semigroup module $ A $ with the aim of explicitly constructing all $ \mathbb {N}^{k} 1 $ -cocycles with values in the $ \mathbb {N}^{k} $ -module $ A $ .

Definition 3.1. (Semigroup cocycles)

Let $ S $ be a semigroup and $ A $ an $ S $ -module, so that $ A $ is an abelian group and there exists a homomorphism $ \pi : S \to \operatorname {End} ({A}) $ . When there is no danger of confusion, for $ s \in S $ and $ \alpha \in A $ , we denote by $ s \alpha \in A $ the element $ [ \pi ({s}) ] ({\alpha }) $ of $ A $ . Define $ Z^{1} ({S,A}) $ to be the set of $ A $ -valued $ 1 $ -cocycles on $ S $ , that is, $ Z^{1} ({S,A}) $ is the set of functions

$$ \begin{align*}Z^{1} ({S,A}) := \{ \gamma: S \to A ~ | ~ \gamma ({st}) = \gamma ({s}) + s \gamma ({t})~\text{for all } s,t \in S \}. \end{align*} $$

A function $ \gamma : S \to A $ is said to be an $ A $ -valued $ 1 $ -coboundary on $ S $ if there is an $ \alpha \in A $ such that $ \gamma ({s}) = \alpha - s \alpha $ for all $ s \in S $ , in which case we write $\gamma = \gamma _{\alpha } $ . Let $ B^{1} ({S,A}) $ denote the collection of all $ A $ -valued $ 1 $ -coboundaries on $ S $ .

Routine computations show that $ Z^{1} ({S,A}) $ forms a group under addition, that every $ 1 $ -coboundary is a $ 1 $ -cocycle, and that $ B^{1} ({S,A}) $ is a subgroup of $ Z^{1} ({S,A}) $ . We verify that every $ 1 $ -coboundary is in fact a $ 1 $ -cocycle. Let $ \alpha \in A $ and $ s,t \in S $ ; then

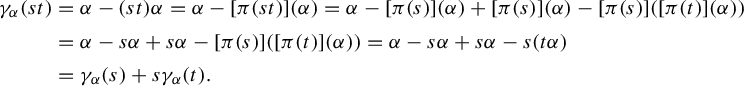$$ \begin{align*} \gamma_{\alpha} ({s t}) & = \alpha - ({s t}) \alpha = \alpha - [ \pi ({st}) ] ({ \alpha}) = \alpha - [ \pi ({s}) ] ({ \alpha}) + [ \pi ({s}) ] ({ \alpha}) - [ \pi ({s}) ] ({[ \pi ({t}) ] ({ \alpha})}) \\ & = \alpha - s \alpha + s \alpha - [ \pi ({s}) ] ({[ \pi ({t}) ] ({ \alpha})}) = \alpha - s \alpha + s \alpha - s ({t \alpha}) \\ & = \gamma_{\alpha} ({s}) + s \gamma_{ \alpha} ({t}). \end{align*} $$

Hence, $ B^{1} ({S,A}) \subseteq Z^{1} ({S,A}) $ . Moreover, we define the first semigroup cohomology of $ S $ with coefficients in $ A $ by $ H^{1} ({S,A}) := Z^{1} ({S,A}) / B^{1} ({S,A}) $ .

For the special case $ S = \mathbb {N}^{k} $ , $k\in \mathbb {N}_{>0}$ , the following definition provides an important example of an $ S $ -module.

Definition 3.2. Let $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ be a $ k $ -tuple of commuting surjective local homeomorphisms on the locally compact Hausdorff space $ X $ . Let $ H $ be a topological locally compact abelian group. Define an $ \mathbb {N}^{k} $ -module structure on $ A = \operatorname {C} ({X,H}) $ by setting

$$ \begin{align*}[ \pi_{n} ({f}) ] ({x}) := f ({\sigma^{n} ({x})}) \end{align*} $$

for all $ n \in \mathbb {N}^{k} $ , $ f \in \operatorname {C} ({X,H}) $ , and $ x \in X $ .

The next condition will be crucial in constructing $ 1 $ -cocycles on $ \mathbb {N}^{k} $ .

Definition 3.3. (Module cocycle condition)

Let $ A $ be an $ \mathbb {N}^{k} $ -module and let $ a=({a_{i}})_{i \in [ k ]} $ be a $ k $ -tuple of elements of $ A $ . We say that $ ({a_{i}})_{i \in [ k ]} $ satisfies the module cocycle condition if for all $i,j \in [k], ~ i \neq j$ ,

(2) $$ \begin{align} a_{i} + \mathbf{e}_{i} a_{j} = a_{j} + \mathbf{e}_{j} a_{i}, \end{align} $$

where $ \{ \mathbf {e}_{i} \}_{i \in [ k ]} $ are the canonical generators of $ \mathbb {N}^{k} $ .

Theorem 3.4. Let $ A $ be an $ \mathbb {N}^{k} $ -module.

1. (1) Suppose that the $ k $ -tuple $ a = ({a_{i}})_{i \in [ k ]} \in A^{k} $ satisfies the module cocycle condition of equation (2). Then there is a unique cocycle $ c_{a} \in Z^{1} ({\mathbb {N}^{k},A}) $ satisfying, for every $\ell \in [ k ]$ ,

   (3) $$ \begin{align} c_{a} ({\mathbf{e}_{\ell}}) = a_{\ell}. \end{align} $$
   The cocycle $ c_{a} $ is given by the following formula:
   (4) $$ \begin{align} c_{a} ({n}) : = \sum_{i = 0}^{n_{1} - 1} \mathbf{e}_{1}^{i} a_{1} + \mathbf{e}_{1}^{n_{1}} \sum_{i = 0}^{n_{2} - 1} \mathbf{e}_{2}^{i} a_{2}\ + \cdots +\ \mathbf{e}_{1}^{n_{1}} \mathbf{e}_{2}^{n_{2}} \cdots \mathbf{e}_{k - 1}^{n_{k - 1}} \sum_{i = 0}^{n_{k} - 1} \mathbf{e}_{k}^{i} a_{k}. \end{align} $$

2. (2) The correspondence between the $ k $ -tuples $ a = ({a_{i}})_{i \in [ k ]} \in A^{k} $ satisfying the module cocycle condition and the associated cocycles $ c_{a} \in Z^{1} ({\mathbb {N}^{k},A}) $ is a bijection.

3. (3) Such a $ 1 $ -cocycle $ c_{a} \in Z^{1} ({\mathbb {N}^{k},A}) $ corresponds to a coboundary in $ B^{1} ({\mathbb {N}^{k},A}) $ if and only there exists $\alpha \in A$ such that $ a_{i} = \alpha - \mathbf {e}_{i} \alpha $ for $ i \in [ k ] $ .

Proof Proof of (1). We subdivide the proof into two parts. We will first prove that the formula for $ c_{a} $ in equation (4) gives a $ 1 $ -cocycle on $ \mathbb {N}^{k} $ satisfying the conditions of equation (3). Then we will prove the uniqueness.

For the first part of the proof, we will proceed by induction. For a fixed $N\in \mathbb {N}$ our induction statement is that for any $t, m,n \in \mathbb {N}^{k} $ , with $ \lvert t \rvert \leq N $ and $ \lvert m + n \rvert \leq N $ , we have

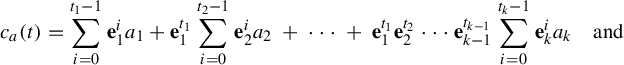(5) $$ \begin{align} c_{a} ({t}) &= \sum_{i = 0}^{t_{1} - 1} \mathbf{e}_{1}^{i} a_{1} + \mathbf{e}_{1}^{t_{1}} \sum_{i = 0}^{t_{2} - 1} \mathbf{e}_{2}^{i} a_{2}\ +\ \cdots\ +\ \mathbf{e}_{1}^{t_{1}} \mathbf{e}_{2}^{t_{2}} \cdots \mathbf{e}_{k - 1}^{t_{k - 1}} \sum_{i = 0}^{t_{k} - 1} \mathbf{e}_{k}^{i} a_{k}\quad\text{and} \end{align} $$

(6) $$ \begin{align} c_{a} ({m + n}) &= c_{a} ({m}) + m\ c_{a} ({n}).\end{align} $$

The base case $N=1$ is easily checked as it amounts to, for all $ \ell \in [ k ] $ ,

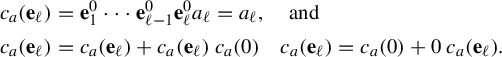$$ \begin{align*} c_{a} ({\mathbf{e}_{\ell}}) &= \mathbf{e}_{1}^{0} \cdots \mathbf{e}_{\ell -1}^{0} \mathbf{e}_{\ell}^{0} a_{\ell} = a_{\ell},\quad\text{and}\nonumber\\ c_{a} ({\mathbf{e}_{\ell} }) &= c_{a} ({\mathbf{e}_{\ell}}) + c_{a}(\mathbf{e}_{\ell} ) \, c_{a} ({ 0})\quad c_{a} ({\mathbf{e}_{\ell} }) = c_{a} ({0}) +0\, c_{a}(\mathbf{e}_{\ell}). \end{align*} $$

For the inductive step, we now suppose that the cocycle formula in equation (5) holds for all $t\in \mathbb {N}^k$ , with $|t|\leq N$ , and that equation (6) holds for all $n,m\in \mathbb {N}^k$ with $ |n+m|\leq N$ . We need to show that equation (5) holds for all $c_a(t)$ , with $|t|\leq N+1$ , and that equation (6) holds for all $n,m\in \mathbb {N}^k$ with $ |n+m|\leq N+1$ . To do so, fix $m, n \in \mathbb {N}$ with $\lvert m +n \rvert = N $ and choose any $ \ell \in [ k ] $ so that $ (m +n +\mathbf {e}_{\ell }) \in \mathbb {N}^k$ , which implies that $\lvert m +n +\mathbf {e}_{\ell } \rvert = N + 1 $ .

Assume first that $m =0.$ Then, since $|n| = N$ , the induction hypothesis (particularly equation (5)) implies that

(7) $$ \begin{align} c_{a} ({\mathbf{e}_{\ell}})\ +\ \mathbf{e}_{\ell}\, c_{a} ({n}) = c_{a} ({\mathbf{e}_{\ell}})\ +\ \mathbf{e}_{\ell} \bigg( \sum_{i = 0}^{n_{1} - 1} \mathbf{e}_{1}^{i} a_{1}\ +\ \cdots \ +\ \mathbf{e}_{1}^{n_{1}} \mathbf{e}_{2}^{n_{2}} \cdots \mathbf{e}_{k - 1}^{n_{k - 1}} \sum_{i = 0}^{n_{k} - 1} \mathbf{e}_{k}^{i} a_{k} \bigg). \end{align} $$

Now note that for $ j < \ell $ , the module cocycle condition of equation (2) implies that

(8) $$ \begin{align} \mathbf{e}_{\ell} \sum_{i = 0}^{n_{j} - 1} \mathbf{e}_{j}^{i} a_{j} = \sum_{i = 0}^{n_{j} - 1} \mathbf{e}_{j}^{i} ({\mathbf{e}_{\ell} a_{j}}) = \sum_{i = 0}^{n_{j} - 1} \mathbf{e}_{j}^{i} ({a_{j} + \mathbf{e}_{j} a_{\ell} - a_{\ell}}) = \sum_{i = 0}^{n_{j} - 1} \mathbf{e}_{j}^{i} a_{j} + \mathbf{e}_{j}^{n_{j}} a_{\ell} - a_{\ell}. \end{align} $$

Next, we will we use equation (8) to replace the terms $ \leq \ell $ in equation (7) with equivalent expressions, to get

(9) $$ \begin{align} c_{a} ({\mathbf{e}_{\ell}}) + \mathbf{e}_{\ell} c_{a} ({n}) &= a_{\ell} + \bigg( \sum_{i = 0}^{n_{1} - 1} \mathbf{e}_{1}^{i} a_{1} + \mathbf{e}_{1}^{n_{1}} a_{\ell} - a_{\ell} \bigg)\nonumber\\ &\quad + \mathbf{e}_{1}^{n_{1}} \bigg( \sum_{i = 0}^{n_{2} - 1} \mathbf{e}_{2}^{i} a_{2} + \mathbf{e}_{j}^{n_{j}} a_{\ell} - a_{\ell} \bigg)\nonumber\\ &\quad + \cdots + \mathbf{e}_{1}^{n_{1} - 1} \mathbf{e}_{2}^{n_{2}} \cdots \mathbf{e}_{\ell - 1}^{n_{\ell - 1}} \bigg( \sum_{i=0}^{n_\ell } \textbf{e}_\ell^i(a_\ell) - a_\ell \bigg)\nonumber\\ &\quad+ \cdots + \mathbf{e}_{\ell} \mathbf{e}_{1}^{n_{1} - 1} \mathbf{e}_{2}^{n_{2}} \cdots \mathbf{e}_{k - 1}^{n_{k - 1}} \sum_{i = 0}^{n_{k} - 1} \mathbf{e}_{k}^{i} a_{k}. \end{align} $$

By using the telescopic properties of equation (9) above, one easily sees that $ c_{a} ({\mathbf {e}_{\ell }}) + \mathbf {e}_{\ell } c_{a} ({n}) $ is equal to

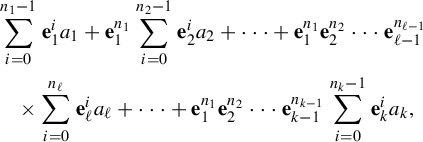$$ \begin{align*} &\sum_{i = 0}^{n_{1} - 1} \mathbf{e}_{1}^{i} a_{1} + \mathbf{e}_{1}^{n_{1}} \sum_{i = 0}^{n_{2} - 1} \mathbf{e}_{2}^{i} a_{2} + \cdots + \mathbf{e}_{1}^{n_{1}} \mathbf{e}_{2}^{n_{2}} \cdots \mathbf{e}_{\ell - 1}^{n_{\ell - 1}}\\ &\quad\times \sum_{i = 0}^{n_{\ell}} \mathbf{e}_{\ell}^{i} a_{\ell} + \cdots + \mathbf{e}_{1}^{n_{1}} \mathbf{e}_{2}^{n_{2}} \cdots \mathbf{e}_{k - 1}^{n_{k - 1}} \sum_{i = 0}^{n_{k} - 1} \mathbf{e}_{k}^{i} a_{k}, \end{align*} $$

which equals $ c_{a} ({\mathbf {e}_{\ell } + n})$ . That is, we have proven that, for $n \in \mathbb {N},$ $\lvert n \rvert = N $ , and any $ \ell \in [ k ] $ ,

(10) $$ \begin{align} c_{a} ({\mathbf{e}_{\ell}})\ +\ \mathbf{e}_{\ell}\, c_{a} ({n})= c_{a} ({\mathbf{e}_{\ell} + n}).\end{align} $$

Moreover, by using equation (5) to replace $c_a(n)$ with the right-hand side of that equation in the above expression, a straightforward calculation shows that equation (5) holds for $t=n+ \mathbf {e}_{\ell }.$

We now suppose that $ m,n \in \mathbb {N}^{k} $ with $ \lvert m + n \rvert = N + 1 $ and $ \lvert m \rvert> 0$ with positive $\ell $ th coordinate $m_\ell $ for some $ \ell \in [ k ] $ . Define $ m' : =\ m- \mathbf {e}_{\ell } \in \mathbb {N}^{k} $ and note that $ \lvert \mathbf {e}_{\ell } + m' + n \rvert = \lvert m + n \rvert - 1 = ({N + 1}) - 1 = N $ . Therefore, by equation (10), we get

$$ \begin{align*}c_{a} ({m + n}) = c_{a} ({\mathbf{e}_{\ell} + m' + n}) = c_{a} ({\mathbf{e}_{\ell}}) + \mathbf{e}_{\ell}\, c_{a} ({m' + n}). \end{align*} $$

By using the induction hypothesis twice, we now get

$$\begin{align*} c_{a} ({m + n}) & = c_{a} ({\mathbf{e}_{\ell}}) + \mathbf{e}_{\ell} ({f ({m'}) + m' c_{a} ({n})}) = c_{a} ({\mathbf{e}_{\ell}}) + \mathbf{e}_{\ell} c_{a} ({m'}) + ({\mathbf{e}_{\ell} + m}) c_{a} ({n}) \nonumber\\ & = c_{a} ({\mathbf{e}_{\ell} + m'}) + ({\mathbf{e}_{\ell} + m}) c_{a} ({n}) = c_{a} ({m}) + m\, c_{a} ({n}). \end{align*}$$

Moreover, by using equation (5) to replace in the above expression $c_a(m)$ and $c_a(n)$ with the right-hand side of that equation, a straightforward calculation shows that equation (5) holds for $t=m+n.$

This completes the inductive step and so we have proven that the formula for $ c_{a} $ in equation (4) gives a $ 1 $ -cocycle on $ \mathbb {N}^{k} $ satisfying the conditions of equation (3).

We now prove the uniqueness. Let $ c_{a} $ be as described above and let $ f $ be any other $ 1 $ -cocycle on $ \mathbb {N}^{k} $ such that $ f ({\mathbf {e}_{i}}) = a_{i} $ for $ i \in [ k ] $ . Now we proceed by induction on the length $ \lvert n \rvert $ of n. The base case that $ c_{a} ({n}) = f ({n}) $ for all $ n \in \mathbb {N}^{k} $ with $ \lvert n \rvert \leq 1 $ follows from the definitions of $ c_{a} $ and $ f $ .

For the inductive step, assume that $ c_{a} ({r}) = f ({r}) $ for all $ r \in \mathbb {N}^{k} $ with $ \lvert r \rvert \leq N $ and suppose that $ \lvert n \rvert = n_{1} + n_{2} + \cdots + n_{k} = N $ and $ \lvert m \rvert = m_{1} + m_{2} + \cdots + m_{k} = N + 1 $ , which implies that $ m = n + \mathbf {e}_{\ell } $ for some $ \ell $ . By using the inductive hypothesis and the module cocycle condition of equation (2), we then get

$$ \begin{align*}f ({m}) = f ({\mathbf{e}_{\ell} + n}) = c_{a} ({\mathbf{e}_{\ell}}) + \mathbf{e}_{\ell} c_{a} ({n}) = c_{a} ({m}). \end{align*} $$

Proof of (2). We have already proven in (1) that the correspondence $a \to c_a$ is injective. To prove that $a \to c_a$ is a surjection onto $ Z^{1} ({\mathbb {N}^{k},A}) $ , let us take $ c \in Z^{1} ({\mathbb {N}^{k},A}) $ and set $ a_{i} := c ({\mathbf {e}_{i}}) $ . It is then easy to check that the $ k $ -tuple $ ({a_{i}})_{i \in [ k ]} $ satisfies the module cocycle condition.

Proof of (3). Suppose that the $ k $ -tuple $a= ({a_{i}})_{i \in [ k ]} \in A^{k} $ gives rise to a coboundary $ c_a $ . Then by definition there exists $\alpha \in A$ such that for all $ i \in [ k ]$ ,

$$ \begin{align*}a_{i}= c_{a} ({\mathbf{e}_{i}}) = \alpha - \mathbf{e}_{i} \alpha. \end{align*} $$

The other direction is clear.

Remark 3.5. In the most important of our uses of the above result, Theorem 3.4 applies to the $\mathbb {N}^k$ -module $A=C(X, \mathbb {R})$ as in Definition 3.2.

3.2 Continuous $ 1 $ -cocycles on $ \mathcal {G} ({X,\sigma }) $

In this subsection, our objective is to give an algebraic way of constructing all continuous $ H $ -valued $ 1 $ -cocycles, where $ H $ is a locally compact abelian group, on groupoids associated to a finite family of commuting local homeomorphisms of a compact metric space. In later sections we will mainly be interested in the case $ H = \mathbb {R} $ . We begin by recalling the definition of these groupoids.

Definition 3.6. [7, 10]

Let $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ be a $ k $ -tuple of commuting surjective local homeomorphisms on the compact Hausdorff space $ X $ . We regard $ \sigma $ as an action of $\mathbb {N}^{k} $ on $ X $ by the formula $ \sigma ^{n} = \sigma _{1}^{n_{1}} \ldots \sigma _{k}^{n_{k}} $ , where $ n = ({n_{i}})_{i \in [ k ]} \in N^{k} $ . The transformation groupoid (also called the semidirect product groupoid of the action) $ \mathcal {G} ({X,\sigma }) $ is defined by

$$ \begin{align*}\mathcal{G} ({X,\sigma}) := \{ ({x,p - q,y}) \in X \times {\mathbb{Z}}^{k} \times X ~ | ~ p,q \in \mathbb{N}^{k} ~ \text{and} ~ \sigma^{p} ({x}) = \sigma^{q} ({y}) \}. \end{align*} $$

We identify $ X $ with the unit space of $ \mathcal {G} ({X,\sigma }) $ via the map $ x \mapsto ({x,0,x}) $ . The structure maps are given by $ r ({x,n,y}) = x $ , $ s ({x,n,y}) = y $ , $ ({x,m,y})^{- 1} = ({y,- m,x}) $ , and $ ({x,m,y}) ({y,n,z}) = ({x,m + n,z}) $ . A basis for the topology on $ \mathcal {G} ({X,\sigma }) $ is given by subsets of the form

$$ \begin{align*}\mathcal{Z} ({U,V,m,n}) := U \times \{ p - q \} \times V, \end{align*} $$

where $ U,V $ are open in $ X $ and $ \sigma ^{p} [ U ] = \sigma ^{q} [ V ] $ . We will denote by $ \mathcal {G} ({X,\sigma })^{({2})} $ the set of composable pairs of $ \mathcal {G} ({X,\sigma }) $ .

The number $ k $ is called the rank of $ \mathcal {G} ({X,\sigma }) $ .

It is well known that $ \mathcal {G} ({X,\sigma }) $ is an étale locally compact Hausdorff amenable groupoid (cf. [7, 26]).

Definition 3.7. (Continuous groupoid 1-cocycles)

Let $ \mathcal {G} $ be a topological groupoid and $ H $ be a topological locally compact abelian group. A continuous $ H $ -valued $ 1 $ -cocycle on $ \mathcal {G} $ is a continuous function $ c: \mathcal {G} \to H $ such that for any $ ({\gamma ,\gamma '}) $ in $ \mathcal {G}^{({2})} $ , we have

$$ \begin{align*}c ({\gamma \gamma'}) = c ({\gamma}) + c ({\gamma'}). \end{align*} $$

In other words, $ c $ is just a continuous groupoid homomorphism from $ \mathcal {G} $ to $ H $ . We will denote by $ Z_{\operatorname {cont}}^{1} ({\mathcal {G},H}) $ the set of continuous $ H $ -valued $ 1 $ -cocycles on $ \mathcal {G} $ .

It is well known that $ Z_{\operatorname {cont}}^{1} ({\mathcal {G},H}) $ is a group under pointwise addition and that $ B_{\operatorname {cont}}^{1} ({\mathcal {G},H}) $ , the collection of continuous functions $ c: \mathcal {G} \to H $ such that there is a continuous function $ f : \mathcal {G}^{({0})} \to H $ such that for all $ \gamma \in \mathcal {G} $ , $ c ({\gamma }) = f ({r ({\gamma })}) - f ({s ({\gamma })}) $ , is a subgroup of $ Z_{\operatorname {cont}}^{1} ({\mathcal {G},H}) $ . We define the first continuous cocycle groupoid cohomology of $ \mathcal {G} $ by

$$ \begin{align*}H_{\operatorname{cont}}^{1} ({\mathcal{G},H}) := Z_{\operatorname{cont}}^{1} ({\mathcal{G},H}) / B_{\operatorname{cont}}^{1} ({\mathcal{G},H}). \end{align*} $$

Our goal is to give an algebraic characterization of the cocycles in $ Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ for $ \mathcal {G} ({X,\sigma }) $ expressed in terms of their coordinate-defining functions as given in (2) below. To do so, we will introduce the following definition, which details a special case of the module cocycle condition.

Definition 3.8. (The cocycle condition)

Let $ H $ be a topological locally compact abelian group. Fix $ k \in \mathbb {N} $ and let $ ({X,\sigma ,\varphi }) $ be an ordered triple with:

1. (1) $ X $ a compact metric space;

2. (2) $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ a $ k $ -tuple of commuting surjective local homeomorphisms of $ X $ ;

3. (3) $ \varphi = ({\varphi _{i}})_{i \in [ k ]} $ a $ k $ -tuple of elements from $ \operatorname {C} ({X,H}) $ .

Then $ ({X,\sigma ,\varphi }) $ is said to satisfy the cocycle condition of order $ k $ if, for all $i,j \in [ k ]$ ,

(11) $$ \begin{align} \varphi_{i} + \varphi_{j} \circ \sigma_{i} = \varphi_{j} + \varphi_{i} \circ \sigma_{j}. \end{align} $$

Note that equation (11) is a special case of the module cocycle condition of Definition 3.3. When the order $ k $ is understood, we will omit it and just say that $ ({X,\sigma ,\varphi }) $ satisfies the cocycle condition. Moreover, with a slight abuse of notation, when X and $\sigma $ are understood, we will also say that $\varphi $ satisfies the cocycle condition.

Example 3.9. With notation as in Definition 3.8, if $ \varphi _{i} $ is constant for each $ i $ , then $ ({X,\sigma ,\varphi }) $ satisfies the cocycle condition.

The cocycle condition will be the characterizing feature for Ruelle triples in the case of a finite family of commuting endomorphisms; see Definition 4.1.

We now show that every groupoid cocycle $ c \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ arises from a $ k $ -tuple of functions $ ({\varphi _{i}})_{i \in [ k ]} $ satisfying the cocycle condition as above, and conversely.

Proposition 3.10. (Cocycle characterization)

Let $ ({X,\sigma ,\varphi }) $ be a triple that satisfies conditions (1), (2), and (3) of Definition 3.8. Then statements (1) and (2) below are equivalent.

1. (1) Algebraic characterization: $ ({X,\sigma ,\varphi }) $ satisfies the cocycle condition.

2. (2) There exists a unique $ c_{X,\sigma ,\varphi } \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ such that $ c ({x,\mathbf {e}_{i},\sigma _{i} ({x})}) = \varphi _{i} ({x}) $ for all $ i \in [ k ] $ and $ x \in X $ .

Moreover, every $ c \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ arises as a $ c_{X,\sigma ,\varphi }$ for some $k-$ tuple $\varphi $ satisfying the cocycle condition. In addition, $c \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ is a $ 1 $ -coboundary if and only if there exists $ \psi \in \operatorname {C} ({X,H})$ such that $ c ({x,\mathbf {e}_{i},\sigma _{i} ({x})}) = \psi ({x}) - \psi ({\sigma _{i} ({x})}) $ for all $i,j \in [ k ]$ .

Proof $ ({1}) \Longrightarrow ({2}) $ : Assume (1). Since $ \varphi =({\varphi })_{i \in [ k ]} $ satisfies the cocycle condition, by Proposition 3.4, there is a unique $ 1 $ -cocycle $ c_{\varphi } $ on $ \mathbb {N}^{k} $ , taking values in the $ \mathbb {N}^{k} $ -module $ \operatorname {C} ({X,H}) $ , that satisfies $ c ({\mathbf {e}_{i}}) = \varphi _{i} $ for $ i \in [ k ] $ . Define $ c_{X,\sigma ,\varphi } \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ , for all $m,n \in \mathbb {N}^{k}$ , by

$$ \begin{align*}c_{X,\sigma,\varphi} ({x,m - n,y}) := [ c_{\varphi} ({m}) ] ({x}) - [ c_{\varphi} ({n}) ] ({y}). \end{align*} $$

We must show that $ c_{X,\sigma ,\varphi } $ is well defined, that is, if there exist $ p,q \in \mathbb {N}^{k} $ with $ ({x,m - n,y}) = ({x,p - q,y}) \in \mathcal {G} ({X,\sigma }) $ , so that $\sigma ^{m} ({x}) = \sigma ^{n} ({y}) $ and $ \sigma ^{p} ({x}) = \sigma ^{q} ({y}) $ , then

$$ \begin{align*}c_{X,\sigma,\varphi} ({x,m - n,y}) = c_{X,\sigma,\varphi} ({x,p - q,y}). \end{align*} $$

For, note that since $ m - n = p - q $ , we have, for all $i \in [ k ]$ ,

$$ \begin{align*}m ({i}) - n ({i}) = p ({i}) - q ({i}), \quad m ({i}) - p ({i}) = n ({i}) - q ({i}). \end{align*} $$

Define $ r \in \mathbb {N}^{k} $ by

$$ \begin{align*} r &= ({r ({1}),r ({2}),\ldots,r ({k})}), \quad \text{where}\\ r ({i})& = \begin{cases} p ({i}) - m ({i}) = q ({i}) - n ({i}) \quad& \text{if} ~ p ({i}) - m ({i})> 0, \\ 0 \quad& \text{if} ~ p ({i}) - m ({i}) \leq 0. \end{cases} \end{align*} $$

It then follows that $ m + r = m \vee p $ and $ n + r = q \vee p $ , where, for $\alpha ,\beta \in \mathbb {N}^k$ , we shall denote by $ \alpha \vee \beta $ the element of $ \mathbb {N}^{k} $ obtained by taking the maximum of the corresponding coordinates in $ \alpha $ and $ \beta $ . Similarly to r, one can also define $ t \in \mathbb {N}^{k} $ such that $ p + t = m \vee p $ and $ q + t = n \vee q $ . Hence, $ m + r = p + t $ and $ n + r = q + t $ .

We now use the cocycle identity for $ c_{\varphi } $ to get, for all $ ({x,m - n,y}) = ({x,p - q,y}) \in \mathcal {G} ({X,\sigma }) $ ,

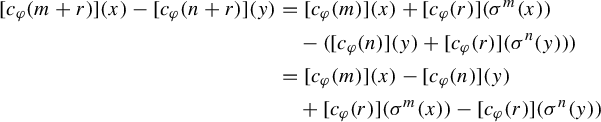$$ \begin{align*} [ c_{\varphi} ({m + r}) ] ({x}) - [ c_{\varphi} ({n + r}) ] ({y}) & = [ c_{\varphi} ({m}) ] ({x}) + [ c_{\varphi} ({r}) ] ({\sigma^{m} ({x})})\\ &\quad- ({[ c_{\varphi} ({n}) ] ({y}) + [ c_{\varphi} ({r}) ] ({\sigma^{n} ({y})})})\\ & = [ c_{\varphi} ({m}) ] ({x}) - [ c_{\varphi} ({n}) ] ({y})\\ &\quad + [ c_{\varphi} ({r}) ] ({\sigma^{m} ({x})}) - [ c_{\varphi} ({r}) ] ({\sigma^{n} ({y})}) \end{align*} $$

and, because $ \sigma ^{m} ({x}) = \sigma ^{n} ({y}) $ , the last two terms cancel each other out.

In the same way we show that $ [ c_{\varphi } ({p + t}) ] ({x}) - [ c_{\varphi } ({q + t}) ] ({y}) = [ c_{\varphi } ({p}) ] ({x}) - [ c_{\varphi } ({q}) ] ({y}) $ .

Therefore, $ c_{X,\sigma ,\varphi } ({x,m - n,y}) = c_{X,\sigma ,\varphi } ({x,p - q,y}) $ , so $ c_{X,\sigma ,\varphi } $ is well defined. Moreover, using the fact that $ c_{\varphi } $ is a cocycle, it easily follows that $ c_{X,\sigma ,\varphi } $ is a cocycle. The fact that $ c_{X,\sigma ,\varphi } $ is continuous follows from the fact that $ c_{\varphi } $ takes values in $ \operatorname {C} ({X,H}) $ .

A straightforward calculation shows that $ c_{X,\sigma ,\varphi } $ is unique. Indeed, any $ c \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ is completely determined by $ \varphi _{i} ({x}): = c ({x,\mathbf {e}_{i},\sigma ^{\mathbf {e}_{i}} ({x})}),\ i \in [ k ], $ and $c=c_{X, \sigma ,\varphi }$ , where $\varphi =( \varphi _i) $ satisfies the cocycle condition.

$ ({2}) \Longrightarrow ({1})$ : Assume (2). Then we have, for all $ i,j \in [ k ] $ and $ x \in X $ , that

$$ \begin{align*} ({x,\mathbf{e}_{i},\sigma_{i} ({x})}) ({\sigma_{i} ({x}),\mathbf{e}_{j},\sigma_{j} ({\sigma_{i} ({x})})}) & = ({x,\mathbf{e}_{i} + \mathbf{e}_{j},\sigma_{j} ({\sigma_{i} ({x})})}) \\ & = ({x,\mathbf{e}_{j} + \mathbf{e}_{i},\sigma_{i} ({\sigma_{j} ({x})})}) \\ & = ({x,\mathbf{e}_{j},\sigma_{j} ({x})}) ({\sigma_{j} ({x}),\mathbf{e}_{i},\sigma_{i} ({\sigma_{j} ({x})})}) \end{align*} $$

and, consequently, for all $ x \in X $ ,

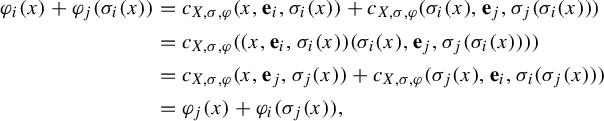$$ \begin{align*} \varphi_{i} ({x}) + \varphi_{j} ({\sigma_{i} ({x})}) & = c_{X,\sigma,\varphi} ({x,\mathbf{e}_{i},\sigma_{i} ({x})}) + c_{X,\sigma,\varphi} ({\sigma_{i} ({x}),\mathbf{e}_{j},\sigma_{j} ({\sigma_{i} ({x})})}) \\ & = c_{X,\sigma,\varphi} ({({x,\mathbf{e}_{i},\sigma_{i} ({x})}) ({\sigma_{i} ({x}),\mathbf{e}_{j},\sigma_{j} ({\sigma_{i} ({x})})})}) \\ & = c_{X,\sigma,\varphi} ({x,\mathbf{e}_{j},\sigma_{j} ({x})}) + c_{X,\sigma,\varphi} ({\sigma_{j} ({x}),\mathbf{e}_{i},\sigma_{i} ({\sigma_{j} ({x})})}) \\ & = \varphi_{j} ({x}) + \varphi_{i} ({\sigma_{j} ({x})}), \end{align*} $$

which yields (1).

The statement about coboundaries is easily checked.

In the particular setting of a groupoid $ \mathcal {G} ({X,\sigma }) $ , with $ A = \operatorname {C} ({X,H}) $ endowed with an $\mathbb {N}^k$ -module structure as in Definition 3.2 and Remark 3.5, Theorem 3.4 specializes to outline the relationship between $ Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ and $\mathbb {N}^k$ -cocycles with values in A.

Corollary 3.11. Let $ \mathcal {G} ({X,\sigma }) $ be a groupoid associated to a k-tuple $\sigma $ of commuting local homeomorphisms of a compact metric space X, and endow $ A = \operatorname {C} ({X,H}) $ with the structure of an $ \mathbb {N}^{k} $ -module as in Definition 3.2. Then there is an isomorphism

$$ \begin{align*}\Phi: Z^{1} ({\mathbb{N}^{k},A}) \longrightarrow Z_{\operatorname{cont}}^{1} ({\mathcal{G} ({X,\sigma}),H}),\quad \Phi ({c_{\varphi}}) : = c_{X, \sigma, \varphi}, \end{align*} $$

where, by means of Theorem 3.4, $ c_{\varphi } \in Z^{1} ({\mathbb {N}^{k},A}) $ is determined by the $ k $ -tuple $\varphi = ({\varphi _{i}})_{i \in [ k ]} \in A^{k} $ and $ c_{X, \sigma , \varphi } $ is the continuous groupoid cocycle associated to $ ({X,\sigma ,\varphi }) $ as in Proposition 3.10.

Moreover, $\Phi $ restricts to an isomorphism between coboundary groups and in addition induces a first cohomology group isomorphism

$$ \begin{align*}\overline{\Phi}: H^{1} ({\mathbb{N}^{k},A}) \cong H_{\operatorname{cont}}^{1} ({\mathcal{G} ({X,\sigma}),H}). \end{align*} $$

Proof It is clear that $\Phi $ preserves the group operations between $ Z^{1} ({\mathbb {N}^{k},A}) $ and $ Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ , and Theorem 3.4 shows that $\Phi $ is a bijection. So, $\Phi $ is an isomorphism. It only remains to show that $\Phi $ induces an isomorphism between $ B^{1} ({\mathbb {N}^k,A}) $ and $B_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ . For, assume that $c_\varphi $ is a coboundary, that is, there exists $ {f } \in A $ such that $c_\varphi =\gamma _f$ , which implies that $ \varphi _{i} = f - \mathbf {e}_{i} f $ for all $ i \in [ k ] $ . Define, for all $i \in [ k ]$ ,

$$ \begin{align*}\varphi_{i} ({x}) = f ({x}) - ({\mathbf{e}_{i} f}) ({x}) = f ({x}) - f ({\sigma^{\mathbf{e}_i} ({x})}). \end{align*} $$

Then the cocycle $c_f := \Phi (c_\varphi )$ is given by, on $ ({x,l,y}) \in \mathcal {G} ({X,\sigma }) $ for $ l = m - n $ with $ \sigma ^{m} ({x}) = \sigma ^{m} ({y}) $ ,

$$ \begin{align*}c_{f} ({x,l,y}) = f ({x}) - f ({y}), \end{align*} $$

which is obviously the coboundary corresponding to $ f \in \operatorname {C} ({X,H}) $ . It is clear that $\Phi $ is one-to-one and onto from $ B^{1} ({\mathbb {N}^{k},\operatorname {C} ({X,H})}) $ to $ B_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ . By the fundamental theorem for group homomorphisms, $\Phi $ also induces an isomorphism

$$ \begin{align*}H^{1} ({\mathbb{N}^{k},\operatorname{C} ({X,H})}) \cong H_{\operatorname{cont}}^{1} ({\mathcal{G} ({X,\sigma}),H}).\\[-42pt] \end{align*} $$

3.3 Cocycles and Ruelle operators

We now use Proposition 3.10 to deduce properties of Ruelle operators corresponding to $ k $ -tuples $\varphi = ({\varphi _{i}})_{i \in [ k ]} $ satisfying the cocycle condition. Recall that by Definition 2.1, the Ruelle operator associated to the Ruelle triple $ ({\tilde {X},\tilde {\sigma },\tilde {\phi }}) $ is denoted by $ \mathcal {L}_{\tilde {X},\tilde {\sigma },\tilde {\phi }} $ .

Theorem 3.12. Let X be a compact Hausdorff space, ${\sigma } =( \sigma _i)_{{i \in [ k ]}}$ be a k-tuple of commuting local homeomorphisms of X, and $\varphi = ({\varphi _{i}})_{i \in [ k ]} $ be a k-tuple of elements of $A=\operatorname {C} ({X,\mathbb {R}})$ .

1. (1) Assume that $\varphi $ satisfies the cocycle condition and let $ c_{\varphi }\in Z^{1} ({\mathbb {N}^{k},A}) $ be the cocycle corresponding to $\varphi $ as in Theorem 3.4. Then the assignment

   $$ \begin{align*} \Psi: \mathbb{N}^{k} \to \operatorname{End} ({\operatorname{C} ({X,\mathbb{R}})}),\quad {\Psi}(n) := \mathcal{L}_{X,\sigma^{n},c_{\varphi} ({n})} \end{align*} $$
   is a semigroup homomorphism.

2. (2) If the k-tuple of Ruelle operators $(\mathcal {L}_{X,\sigma ^{\mathbf {e_i}},\varphi _i })_{i \in [ k ]}$ commutes, then $\varphi $ satisfies the cocycle condition.

Proof For the proof of (1), see Lemma 2.2, which relies on [10, Proposition 2.2] (this latter reference was pointed out to us by the referee, whom we thank for it).

To prove (2), let $ i,j \in [ k ] $ , $ x \in X $ , and $ z = ({\sigma _{i} \circ \sigma _{j}}) ({x}) $ . As the set

$$ \begin{align*}S = ({\sigma_{i} \circ \sigma_{j}})^{- 1} [ \{ z \} ] = ({\sigma_{j} \circ \sigma_{i}})^{- 1} [ \{ z \} ] \end{align*} $$

is finite, we can use Urysohn’s lemma to find an $ f \in \operatorname {C} ({X,\mathbb {R}}) $ such that $ f ({x}) = 1 $ and $ f ({y}) = 0 $ for all $ y \in S \setminus \{ x \} $ . Then

$$ \begin{align*} e^{\varphi_{i} ({\sigma_{j} ({x})}) + \varphi_{j} ({x})} & = [ ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}} \circ \mathcal{L}_{X,\sigma_{j},\varphi_{j}}}) ({f}) ] ({z}) \\ & = [ ({\mathcal{L}_{X,\sigma_{j},\varphi_{j}} \circ \mathcal{L}_{X,\sigma_{i},\varphi_{i}}}) ({f}) ] ({z}) \\ & = e^{\varphi_{j} ({\sigma_{i} ({x})}) + \varphi_{i} ({x})}, \end{align*} $$

which implies that $ \varphi _{i} ({\sigma _{j} ({x})}) + \varphi _{j} ({x}) = \varphi _{j} ({\sigma _{i} ({x})}) + \varphi _{i} ({x}) $ . As $ x \in X $ is arbitrary, we have proved equation (11).

4 $ k $ -Ruelle dynamical systems

We now introduce the main objects of our study: $ k $ -Ruelle dynamical systems, which are higher-rank analogues of Ruelle triples.

Definition 4.1. (k-Ruelle dynamical systems)

A $ k $ -Ruelle dynamical system is an ordered triple $ ({X,\sigma ,\varphi }) $ that satisfies conditions (1), (2), and (3) of Definition 3.8 and the cocycle condition. For a $ k $ -Ruelle dynamical system $ ({X,\sigma ,\varphi }) $ , we will denote by $ c_{X,\sigma ,\varphi } $ the unique $ c \in Z_{\operatorname {cont}}^{1} ({\mathcal {G} ({X,\sigma }),H}) $ such that for all $ i \in [ k ] $ and $ x \in X $ , we have

$$ \begin{align*}c ({x,\mathbf{e}_{i},\sigma_{i} ({x})}) = \varphi_{i} ({x}). \end{align*} $$

Note that the existence of such a $ 1 $ -cocycle is guaranteed by Proposition 3.10.

In Definition 4.1, we could have replaced the cocycle condition by any of its equivalent formulations in Proposition 3.10. However, the cocycle condition usually is the easiest of the three equivalent conditions in Proposition 3.10 to verify and work with.

In analogy with triples that satisfy the unique positive eigenvalue condition of Definition 2.3, we have the following definition.

Definition 4.2. A $ k $ -Ruelle dynamical system $ ({X,\sigma ,\varphi }) $ is said to admit a unique solution for the positive eigenvalue problem of the dual of the Ruelle operator if there exists a unique ordered pair $ ({\boldsymbol {\unicode{x3bb} }^{X,\sigma ,\varphi },\mu ^{X,\sigma ,\varphi }}) $ with the following properties.

1. (1) ${\boldsymbol {\unicode{x3bb} }^{X,\sigma ,\varphi } }= ({\unicode{x3bb} _{i}^{X,\sigma ,\varphi }})_{i \in [ k ]} $ is a $ k $ -tuple of positive real numbers.

2. (2) $ \mu ^{X,\sigma ,\varphi } $ is a Borel probability measure on $ X $ .

3. (3) If $({\mathcal {L}_{X,\sigma _{i},\varphi _{i}}})^{\ast }$ denotes the dual of the Ruelle operator, then, for each $ i \in [ k ] $ ,

   

The next result is the $ k $ -tuple version of Theorem 2.4.

Theorem 4.3. A $ k $ -Ruelle dynamical system $ ({X,\sigma ,\varphi }) $ satisfies Definition 4.2 if there exists $ n \in \mathbb {N}^{k} \setminus \{ 0 \} $ such that $ ({X,\sigma ^{n},c_{\varphi } ({n})}) $ satisfies the unique positive eigenvalue condition of Definition 2.3.

Proof Suppose that there is an $ n \in \mathbb {N}^{k} \setminus \{ 0 \} $ such that $ ({X,\sigma ^{n},c_{\varphi } ({n})}) $ , with ${\varphi _i=c_{\varphi }}(\mathbf {e_{i}}) $ , is a triple that satisfies the unique positive eigenvalue condition of Definition 2.3. Theorem 3.12 tells us that, for all $i \in [k]$ , $\mathcal {L}_{X,\sigma ^{\mathbf {e}_{i}},\varphi _{i}} $ and $ \mathcal {L}_{X,\sigma ^{n},c_{\varphi } ({n})} $ commute, which implies that $ \mathcal {L}_{X,\sigma ^{\mathbf {e}_{i}},\varphi _{i}}^{\ast } $ and $ \mathcal {L}_{X,\sigma ^{n},c_{\varphi } ({n})}^{\ast } $ also commute, and that

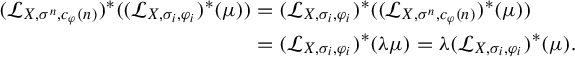$$ \begin{align*} ({\mathcal{L}_{X,\sigma^{n},c_\varphi ({{n}})}})^{\ast} ({({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu})}) & = ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({({\mathcal{L}_{X,\sigma^{n},c_\varphi ({{n}})}})^{\ast} ({\mu})}) \\ & = ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\unicode{x3bb} \mu}) = \unicode{x3bb} ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu}). \end{align*} $$

Hence, $ ({\mathcal {L}_{X,\sigma _{i},\varphi _{i}}})^{\ast } ({\mu }) $ is an eigenmeasure of $ ({\mathcal {L}_{X,\sigma ^{n},c_\varphi ({{n}})}})^{\ast } $ with eigenvalue $ \unicode{x3bb} $ . As we have for all $ f \in \operatorname {C} ({X,\mathbb {R}_{\geq 0}}) $ that

$$ \begin{align*}\int_{X} f ~ \mathrm{d} ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu}) = \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({f}) ~ \mathrm{d} \mu \geq 0, \end{align*} $$

it follows that $ ({\mathcal {L}_{X,\sigma _{i},\varphi _{i}}})^{\ast } ({\mu }) $ is a non-negative measure on $ X $ . Furthermore, by the surjectivity of $ \sigma _{i} $ ,

$$ \begin{align*}\int_{X} 1_{X} ~ \mathrm{d} ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu}) = \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu> 0, \end{align*} $$

where we denote by $1_{X}$ the characteristic function of X. It follows that

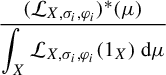$$ \begin{align*}\frac{({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu})}{\displaystyle \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu} \end{align*} $$

is a probability eigenmeasure of $ ({\mathcal {L}_{X,\sigma ^{n},c_\varphi ({{{n}}})}})^{\ast } $ with eigenvalue $ \unicode{x3bb} $ . Since $ ({X,\sigma ^{n},c_{\varphi } ({n})}) $ satisfies Definition 2.3, we must have

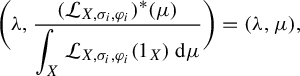$$ \begin{align*}\bigg({\unicode{x3bb}},{\frac{({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu})}{\displaystyle \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu}}\bigg) = ({\unicode{x3bb},\mu}), \end{align*} $$

which yields

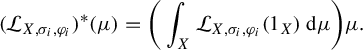$$ \begin{align*}({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu}) = \bigg( \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu \bigg) \mu. \end{align*} $$

Now, if $ \alpha = ({\alpha _{i}})_{i \in [ k ]} $ is a $ k $ -tuple in $ \mathbb {R}_{> 0} $ , and $ \nu $ a probability Borel measure on $ X $ such that for all $ i \in [ k ] $ ,

$$ \begin{align*}({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\nu}) = \alpha_{i} \nu, \end{align*} $$

then, by Theorem 3.12, we get, if we set $\alpha =(\alpha _1,\ldots , \alpha _k)$ ,

$$ \begin{align*}({\mathcal{L}_{X,\sigma^{n},c_{\varphi} ({n})}})^{\ast} ({\nu}) = \alpha^{n} \nu. \end{align*} $$

As $ \alpha ^{n}> 0 $ and $ ({X,\sigma ^{n},c_\varphi ({n})}) $ satisfies Definition 2.3, we also obtain $ ({\alpha ^{n},\nu }) = ({\unicode{x3bb} ,\mu }) $ , so $ \nu = \mu .$ Hence, for all $ i \in [ k ] $ ,

$$ \begin{align*}\alpha_{i} \mu = \bigg( \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu \bigg) \mu, \end{align*} $$

which yields $ \alpha _{i} = \int _{X} \mathcal {L}_{X,\sigma _{i},\varphi _{i}} ({1_{X}}) ~ \mathrm {d} \mu $ for all $ i \in [ k ] $ .

We will now give two examples of $ k $ -Ruelle dynamical systems.

Example 4.4. For $ k \in \mathbb {N}_{> 1} $ , let $ X := \mathbb {Z}_{k}^{\mathbb {N}_{> 0}} $ be equipped with the product topology, where $ {\mathbb {Z}}_{k} := {\mathbb {Z}} / k {\mathbb {Z}} $ . It is well known that the cylinder sets of X form a basis for the topology on X; recall that every finite word $\alpha \in ({\mathbb {Z}}_k)^m$ defines an associated cylinder set $\mathcal {Z}[\alpha ]$ by

$$ \begin{align*}\mathcal{Z}[\alpha] : = \{x\in X\ |\ (x_j)_{j=1,\ldots, m}= \alpha \}.\end{align*} $$

Define a commuting $ k $ -tuple $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ of surjective local homeomorphisms on $ X $ by

$$ \begin{align*}\text{for all } i \in [ k ]\quad\text{for all } x \in X: \sigma_{i} ({x}) := ({x_{n + 1} + ({i - 1})})_{n \in \mathbb{N}_{> 0}}. \end{align*} $$

We want to verify Definition 2.5. To do so, we first check that $ \sigma _{i} $ is positively expansive and exact for each $ i \in [ k ] $ , and subsequently verify that $ \varphi $ is Hölder-continuous.

A straightforward calculation shows that, if we define $ U :=\{ ({x,y}) \in X \times X ~ | ~ x_{1} = y_{1} \} $ , then

$$ \begin{align*}\Delta ({X}) \subseteq U = \bigcup_{i \in [ k ]} \mathcal{Z}[i] \times \mathcal{Z}[i]. \end{align*} $$

To deduce that $ \sigma _{i} $ is positively expansive for each $ i \in [ k ] $ , simply observe that if $ x,y \in X $ are distinct, then $ ({\sigma _{i}^{m - 1} ({x}),\sigma _{i}^{m - 1} ({y})}) \notin U $ , where $ m := \min ({\{ n \in \mathbb {N}_{> 0} ~ | ~ x_{n} \neq y_{n} \}}) $ .

Now we will show that $ \sigma _{i} $ is exact for each $ i \in [ k ] $ . Let $U \subseteq X$ be a non-empty open set. Since the cylinder sets form a basis for the topology on X, there is a cylinder set $\mathcal {Z}[\alpha ] \subseteq U,$ with $|\alpha |=m,$ for some $m \in \mathbb {N}_{>0}.$ Then $ \sigma _{i}^{m} [ U ] \supset \sigma _{i}^{m} [ \mathcal {Z}[\alpha ] ]= X $ , which means that $ \sigma _{i} $ is exact for each $ i \in [ k ] $ .

Let $ d: X \times X\to \mathbb {R}_{\geq 0} $ denote the compatible metric on $ X $ defined by, for all $x,y \in X$ ,

$$ \begin{align*}d ({x,y}) := 2^{- \min ({\{ n \in \mathbb{N}_{> 0} ~ | ~ x_{n} \neq y_{n} \}})}, \end{align*} $$

where $ \min ({\varnothing }) := \infty $ by convention.

Now let $ ({a_{i}})_{i \in [ k ]} \in \mathbb {R}^{k} $ and define $ \varphi : X \to \mathbb {R} $ by, for all $i \in [ k ],~\text {for all } x \in X$ ,

$$ \begin{align*}\varphi ({x}) := a_{i} \iff \sum_{n = 1}^{k} x_{n} = i - 1 ~ ({\text{mod}~k}). \end{align*} $$

Clearly, $ \varphi $ is continuous. Indeed, we note that the value of $ \varphi $ at $ x\in X $ depends only on the first $ k $ components of $ x $ , so that if $ x,y \in X$ and $ d ({x,y}) < 2^{- k} $ , then $ \varphi ({x}) = \varphi ({y}) $ , so that $ \lvert \varphi ({x}) - \varphi ({y}) \rvert = 0 $ in that case. One therefore computes, for all $ x,y \in X $ ,

$$ \begin{align*}\lvert \varphi ({x}) - \varphi ({y}) \rvert \leq 2^{k} ({\max_{i,j \in [ k ]} \lvert a_{i} - a_{j} \rvert}) d ({x,y}), \end{align*} $$

which implies that $ \varphi $ is Hölder-continuous with respect to $ d $ .

Let $ ({c_{i}})_{i \in [ k ]} \in \mathbb {R}^{k} $ . Then, for all $ i,j \in [ k ] $ and for all $ x \in X $ ,

$$ \begin{align*}({\varphi + c_{i} 1_{X}}) ({\sigma_{j} ({x})}) - ({\varphi + c_{j} 1_{X}}) ({\sigma_{i} ({x})}) \kern1.3pt{=}\kern1.3pt ({\varphi ({\sigma_{i} ({x})}) + c_{i}}) - ({\varphi ({\sigma_{j} ({x})}) + c_{j}}) \kern1.3pt{=}\kern1.3pt c_{i} - c_{j}, \end{align*} $$

the final equality holding because $ \varphi ({\sigma _{i} ({x})}) = \varphi ({\sigma _{j} ({x})}) $ . Therefore, $(X,({\sigma _{i}})_{i \in [ k ]}, ({\varphi + c_{i} 1_{X}})_{i \in [ k ]}) $ is a Ruelle dynamical system and, since the Ruelle triple $ ({X,\sigma _{i},\varphi _{i}}) $ satisfies the conditions of Definition 2.5 for each $ i \in [ k ] $ , we conclude that $ (X,({\sigma _{i}})_{i \in [ k ]}, ({\varphi + c_{i} 1_{X}})_{i \in [ k ]}) $ satisfies the unique positive eigenvalue condition of Definition 2.3.

The next example exhibits a dynamical system on a non-Cantor space admitting a unique solution to the positive eigenvalue problem.

Example 4.5. Let $ n = ({n_{i}})_{i \in [ k ]} $ be a $ k $ -tuple, $ n_{i} \in {\mathbb {Z}} \setminus \{ 0,\pm 1 \} $ , and define a commuting $ k $ -tuple $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ of surjective local homeomorphisms on $ \mathbb {T} $ by, for all $i \in [ k ]$ and for all $z \in \mathbb {T}$ , $\sigma _{i} ({z}) := z^{n_{i}}.$ The local homeomorphism $ \sigma _{i} $ is expansive for each $ i \in [ k ] $ by [29, top of p. 176]. Now let $ U $ be a non-empty open subset of $ \mathbb {T} $ . Then there exist $ \alpha ,\beta \in \mathbb {R} $ such that $ \alpha < \beta $ and

$$ \begin{align*}\{ e^{\textrm{i} \theta} \in \mathbb{T} ~ | ~ \alpha < \theta < \beta \} \subseteq U. \end{align*} $$

Let $ i \in [ k ] $ and let $ m \in \mathbb {N} $ be such that $ 2 \pi \leq m \lvert n_{i} \rvert ({\beta - \alpha }) $ . Then

$$ \begin{align*} \sigma_{i}^{m} [ U ] & \supseteq \sigma_{i}^{m} [ \{ e^{\textrm{i} \theta} \in \mathbb{T} ~ | ~ \alpha < \theta < \beta \} ] = \{ e^{\textrm{i} m n_{i} \theta} \in \mathbb{T} ~ | ~ \alpha < \theta < \beta \} \\ & = \{ e^{\textrm{i} \theta} \in \mathbb{T} ~ | ~ \theta ~ \text{between} ~ m n_{i} \alpha ~ \text{and} ~ m n_{i} \beta \} = \mathbb{T}, \end{align*} $$

so $ \sigma _{i} $ is exact.

Let $ d $ denote the metric on $ \mathbb {T} $ , defined by, for all $ \alpha ,\beta \in \mathbb {R} $ ,

$$ \begin{align*}d(e^{i\alpha},e^{i\beta})= \text{inf}\{|\alpha-(\beta+n\pi)| : n\in\mathbb Z\}.\end{align*} $$

The metric $ d $ generates the standard topology on $ \mathbb {T} $ .

Define a $ k $ -tuple $ \varphi = ({\varphi _{i}})_{i \in [ k ]} $ in $ \operatorname {C} ({X,\mathbb {C}}) $ by, for all $i \in [ k ], ~ \text { for all } z \in \mathbb {T}$ , $\varphi _{i} ({z}) = z^{n_{i}} - z.$ A straightforward calculation shows that $ \varphi _{i} $ is Hölder-continuous with respect to $ d $ for each $ i \in [ k ] $ and that the ( $ \mathbb {C} $ -valued) cocycle condition $ \varphi _{i} + \varphi _{j} \circ \sigma _{i} = \varphi _{j} + \varphi _{i} \circ \sigma _{j}$ holds.

Now let $ f: \mathbb {C} \to \mathbb {R} $ be a continuous additive map (e.g., $ f ({z}) = {\mathrm {Re}}(z) $ ). As $ f $ is then Hölder-continuous with respect to the Euclidean metrics on $ \mathbb {C} $ and $ \mathbb {R} $ , $ f \circ \varphi _{i} $ is also Hölder-continuous with respect to $ d $ and, by the additivity of $ f $ , for every $i,j \kern1.2pt{\in}\kern1.2pt [ k ] $ ,

$$ \begin{align*} ({f \circ \varphi_{i}}) + ({f \circ \varphi_{j}}) \circ \sigma_{i} &= f \circ ({\varphi_{i} + \varphi_{j} \circ \sigma_{i}}) = f \circ ({\varphi_{j} + \varphi_{i} \circ \sigma_{j}})\\ &= ({f \circ \varphi_{j}}) + ({f \circ \varphi_{i}}) \circ \sigma_{j}, \end{align*} $$

so that $ ({\mathbb {T},\sigma ,({f \circ \varphi _{i}})_{i \in [ k ]}}) $ is a Ruelle dynamical system. As the Ruelle triple $ ({\mathbb {T},\sigma _{i},f \circ \varphi _{i}}) $ satisfies the conditions in Definition 2.5 for each $ i \in [ k ] $ , we conclude that $ ({\mathbb {T},\sigma ,({f \circ \varphi _{i}})_{i \in [ k ]}}) $ has a unique eigenmeasure as in Definition 4.2.

Example 4.6. Fixing $ d \in \mathbb {N} $ , where $ d> 1 $ , define two commuting local homeomorphisms $ \sigma _{1} $ and $ \sigma _{2} $ of $ \mathbb {T}^{2} $ by, for all $z_{1},z_{2} \in \mathbb {T}$ ,

$$ \begin{align*}\sigma_{1} ({z_{1},z_{2}}) := ({z_{1}^{d},z_{2}^{d}}), \quad \sigma_{2} ({z_{1},z_{2}}) := ({z_{1} z_{2}^{- 1},z_{1} z_{2}}). \end{align*} $$

Since all the eigenvalues of the associated matrices $ M_{\sigma _{1}} := \big [\begin {smallmatrix} d & 0 \\ 0 & d \end {smallmatrix}\big ] $ and $ M_{\sigma _{2}} := \big [\begin {smallmatrix} 1 & - 1 \\ 1 & 1 \end {smallmatrix}\big ] $ have modulus larger than one, $ \sigma _{1} $ and $ \sigma _{2} $ are toral endomorphisms that are positively expansive and exact (see [19, Proof of Theorem 1]). In this case, we can choose the functions $ \varphi _{j} := c_{j} 1_{\mathbb {T}^{2}} $ to be constant functions. Therefore, the Ruelle triple $ ({\mathbb {T}^{2},\sigma _{i},c_{i} 1_{\mathbb {T}^{2}}}) $ satisfies the conditions of Definition 2.5 for each $ i \in \{ 1,2 \} $ .

The next example is a combination of Examples 4.5 and 4.4.

Example 4.7. Let $ X := {\mathbb {Z}}_{k}^{\mathbb {N}_{> 0}} $ with $ k \in \mathbb {N}_{> 1} $ . Fixing $ I \in [ k ] $ and $ J \in \mathbb {N}_{> 1} $ , define local homeomorphisms $ \sigma _{I},\sigma _{J}: X \times \mathbb {T} \to X \times \mathbb {T} $ by the following formula. For all $ ({x,z}) \in X \times \mathbb {T} $ , set

$$\begin{align*}\sigma_{I} ({x,z}) & := ({({x_{n + 1} + ({I - 1})})_{n \in \mathbb{N}_{> 0}},z}), \nonumber\\ \sigma_{J} ({x,z}) & := ({x,z^{J}}).\end{align*}$$

It is clear that $ \sigma _{I} $ and $ \sigma _{J} $ commute and one calculates that the composition $ \sigma _{I} \circ \sigma _{J} $ is positively expansive and exact. By proceeding as in Examples 4.5 and 4.4, and using Theorem 4.3 with $ k = 2 $ and $ ({n_{1},n_{2}}) = ({1,1}) $ , the resulting Ruelle triple satisfies the conditions in Definition 2.5.

Example 4.8. We will now compute Ruelle eigenvalues and eigenmeasures for the $ k $ -Ruelle dynamical system $ ({X,\sigma ,\varphi }) $ , with $ X = \prod _{j \in \mathbb {N}} \{ 0,1 \} $ , where $ \{ 0,1 \} = {\mathbb {Z}}_2 $ , and $ \sigma = ({\sigma _{1},\sigma _{2}}) $ is defined by, for $ x = ({x_{n}})_{n \in \mathbb {N}} $ ,

$$ \begin{align*}\sigma_{1} ({x}) := ({x_{n + 1}})_{n \in \mathbb{N}}, \quad \sigma_{2} ({x}) := ({x_{n} + 1})_{n \in \mathbb{N}}. \end{align*} $$

Moreover, for $ a,b,c \in \mathbb {R} $ , define $ \varphi = ({\varphi _{1},\varphi _{2}}) $ by the following equation, where below addition is considered modulo two:

(12) $$ \begin{align} \varphi_{1} ({x}) := \begin{cases} a \quad& \text{if} ~ x_{0} + x_{1} = 0, \\ b \quad& \text{if} ~ x_{0} + x_{1} = 1, \end{cases} \quad \varphi_{2} ({x}) := c. \end{align} $$

Firstly, it is a simple exercise to determine that the eigenvalues $ \unicode{x3bb} _{1},\unicode{x3bb} _{2} $ of the associated Ruelle operator are given by $ \unicode{x3bb} _{1} = e^{a} +e^{b} $ and $ \unicode{x3bb} _{2} = e^{c} $ , and that $ \mu ({Z ({0})}) = \mu ({Z ({1})}) = \tfrac 12 $ .

Moreover, the eigenmeasure $ \mu $ on all of the cylinder sets can be computed by using induction, thus proving that $ \mu $ is defined on the cylinder sets of $ X $ according to the following probability diagram and formula. We leave the details of this calculation to the reader.

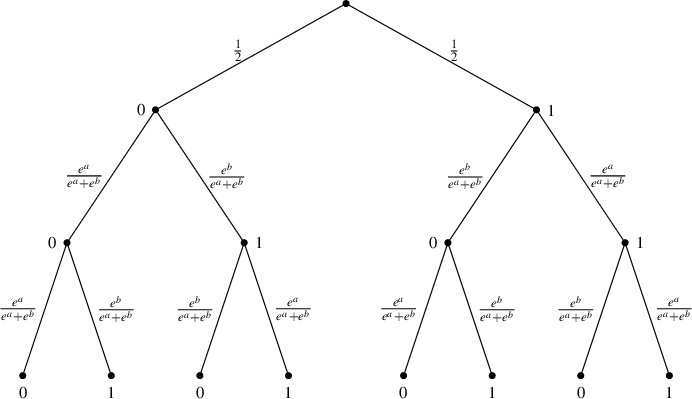
(13) $$ \begin{align} \mu ({Z ({x_{0} x_{1} \cdots x_{n}})}) = \frac{1}{2} \prod_{j = 0}^{n - 1} \frac{e^{\psi ({x_{j} + x_{j + 1}})}}{e^{a} +e^{b}}, \end{align} $$

where $ \psi : \{ 0,1 \} \to \{ a,b \} $ is defined by $ \psi ({0}) := a $ and $ \psi ({1}) := b $ .

In the above formula, note that when $ n = 0 $ , the resulting product is empty and so by convention equal to $ 1 $ . Therefore, $ \mu ({Z ({x_{0}})}) = \tfrac 12 $ for all $ x_{0} \in \{ 0,1 \} $ .

5 The Radon–Nikodym problem and KMS states

This section addresses the Radon–Nikodym problem for groupoids associated to a finite family of commuting local homeomorphisms of a compact metric space, which provides a link between quasi-invariant measures for these groupoids and KMS states for a generalized gauge dynamics on the associated $ C^{\ast } $ -algebra. As a result, there will be a heavier emphasis on measure theory and topology than the previous sections.

Definition 5.1. (Pull-back and quasi-invariant measures)

Let $ \mu $ be a Borel probability measure defined on the Borel sets of the compact metric space $ X $ with associated Borel $ \sigma $ -algebra $ \mathscr {B} ({X}) $ and let $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ be a commuting $ k $ -tuple of surjective local homeomorphisms on $ X $ . Define regular Borel measures $ s^{\ast } \mu $ and $ r^{\ast } \mu $ on $ \mathcal {G} ({X,\sigma }) $ by, for all $ B \in \mathscr {B} ({\mathcal {G} ({X,\sigma })}) $ ,

$$ \begin{align*} ({s^{\ast} \mu}) ({B}) & := \int_{X} \bigg( \sum_{\gamma \in \mathcal{G} ({X,\sigma})_{x}} 1_{B} ({\gamma}) \bigg) ~ \mathrm{d} \mu ({x}), \\ ({r^{\ast} \mu}) ({B}) & := \int_{X} \bigg( \sum_{\gamma \in \mathcal{G} ({X,\sigma})^{x}} 1_{B} ({\gamma}) \bigg) ~ \mathrm{d} \mu ({x}), \end{align*} $$

where we denote by $ \mathcal {G} ({X,\sigma })_{x} $ (respectively $ \mathcal {G} ({X,\sigma })^{x} $ ) the set of arrows in $ \mathcal {G} ({X,\sigma }) $ with source $ x $ (respectively range $ x $ ). We then say that $ \mu $ is quasi-invariant for $ \mathcal {G} ({X,\sigma })$ if $ s^{\ast } \mu $ and $ r^{\ast } \mu $ are equivalent to one another, in which case a Radon–Nikodym derivative for $ \mu $ is any measurable function on $ \mathcal {G} ({X,\sigma }) $ in the same equivalence class (with respect to the equivalence relation module sets of measure zero) as ${\mathrm {d} r^{\ast } \mu }/{\mathrm {d} s^{\ast } \mu }$ [22, §3].

The following lemma will be used in the proof of Theorem 5.3. Its proof follows from the definition of local homeomorphism and the fact that $ X $ is compact.

Lemma 5.2. Let $ T: X \to Y $ be a local homeomorphism of topological spaces from the compact metric space $ X $ to the metric space $ Y $ . Then $ \sup _{y \in Y} \textsf {Card} ({T^{- 1} [ \{ y \} ]}) < \infty $ .

The following theorem is a generalization of Proposition 4.2 of [24] from Deaconu–Renault groupoids to groupoids $ \mathcal {G} ({X,\sigma }) $ and characterizes the solutions of the Radon–Nykodym problem in this general setting. Its proof is quite technical, although in part it is possible to rely on the steps given in Renault’s proof in [24].

Theorem 5.3. Let $ ({X,\sigma ,\varphi }) $ be a $ k $ -Ruelle dynamical system, which satisfies the conditions of Definition 4.2, and $ \mu $ a Borel probability measure on $ X $ . Then the following statements are equivalent.

1. (1) $ \mu $ is quasi-invariant for $\mathcal {G} ({X,\sigma }) $ and the Radon–Nikodym derivative $ {\mathrm {d} r^{\ast } \mu }/{\mathrm {d} s^{\ast } \mu } $ is the continuous function $ e^{c_{X,\sigma ,\varphi }} $ on $ \mathcal {G} ({X,\sigma }) $ .

2. (2) $ ({\mathcal {L}_{X,\sigma _{i},\varphi _{i}}})^{\ast } ({\mu }) = \mu $ for each $ i \in [ k ] $ .

Proof Assume that (1) holds and fix $ i \in [ k ] $ ; then $ \mu $ is quasi-invariant for the subgroupoid

$$ \begin{align*}\mathcal{G} ({X,\sigma_{i}}) := \{ ({x,\ell \mathbf{e}_{i},y}) ~ | ~ x,y \in X, ~ m,n \in \mathbb{N}, ~ \ell = m - n, ~ \sigma_{i}^{m} ({x}) = \sigma_{i}^{n} ({y}) \} \end{align*} $$

of $ \mathcal {G} ({X,\sigma }) $ determined by the singly generated system $ ({X,\sigma _{i}}) $ . Thus, by Proposition 4.2 of [24] and using its notation, we have that $^{t}\mathcal {L}_{\varphi _i} ({\mu }) = \mu ,$ which in our notation means that $ ({\mathcal {L}_{X,\sigma _{i},\varphi _{i}}})^{\ast } ({\mu }) = \mu $ . So, $ ({1}) \Longrightarrow ({2})$ .

Conversely, assume that (2) holds. We first briefly explain why $ \mu $ is quasi-invariant for $ \mathcal {G} ({X,\sigma }) $ . A straightforward calculation shows that for all $ i \in [ k ] $ , $ f \in \operatorname {C} ({X,\mathbb {R}}) $ , and $ x \in X $ , we have

$$ \begin{gather*} \int_{X} f ~ \mathrm{d} ({({\sigma_{i}})_{\ast} \mu}) = \int_{X} f \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu. \end{gather*} $$

The Riesz representation theorem then implies that for all $ A \in \mathscr {B} ({X}) $ ,

$$ \begin{align*}({({\sigma_{i}})_{\ast} \mu}) ({A}) = \int_{X} 1_{A} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({1_{X}}) ~ \mathrm{d} \mu, \end{align*} $$

which yields $ ({\sigma _{i}})_{\ast } \mu = \mu \circ \sigma _{i}^{- 1} \ll \mu $ for $ i \in [ k ] $ . On the other hand, $ \mu \ll \mu \circ \sigma _{i}^{- 1} $ for $ i \in [ k ] $ by Proposition 4.2 of [24]. By Lemma 5.2, we now get that for all $ B \in \mathscr {B} ({\mathcal {G} ({X,\sigma })}) $ and some $N\in \mathbb {N}_{>0}$ ,

$$ \begin{align*}\mu ({s [ B ]}) \leq ({s^{\ast} \mu}) ({B}) \leq N \mu ({s [ B ]}), \end{align*} $$

which implies that $ \mu ({s [ B ]}) = 0 $ if and only if $ ({s^{\ast } \mu }) ({B}) = 0 $ ; using a similar technique, we can also prove that $ \mu ({r [ B ]}) = 0 $ if and only if $ ({r^{\ast } \mu }) ({B}) = 0 $ . Finally, by the monotonicity and countable additivity of $ \mu $ , we have for all $ B \in \mathscr {B} ({\mathcal {G} ({X,\sigma })}) $ that

$$ \begin{align*}\mu ({s [ B ]}) \leq {\mu}\bigg({\bigcup_{m,n \in \mathbb{N}^{k}} ({\sigma^{m}})^{- 1} [ \sigma^{n} [ r [ B ] ] ]}\bigg) = 0, \end{align*} $$

so that if $ \mu ({r [ B ]}) = 0 $ , then $ \mu ({s [ B ]}) = 0 $ , and the same method shows that if $ \mu ({s [ B ]}) = 0 $ , then $ \mu ({r [ B ]}) = 0 $ . All of these facts taken together imply that for a fixed $ B \in \mathscr {B} ({\mathcal {G} ({X,\sigma })}) $ , we have $ ({r^{\ast } \mu }) ({B}) = 0 $ if and only if $ ({s^{\ast } \mu }) ({B}) = 0 $ , so $ r^{\ast } \mu $ and $ s^{\ast } \mu $ are equivalent Borel measures on $ \mathcal {G} ({X,\sigma }) $ . Therefore, $ \mu $ is quasi-invariant for $ \mathcal {G} ({X,\sigma }) $ .

Now, by (2), we have for all $ f \in \operatorname {C} ({X,\mathbb {R}}) $ and every $ i \in [ k ] ,$ that

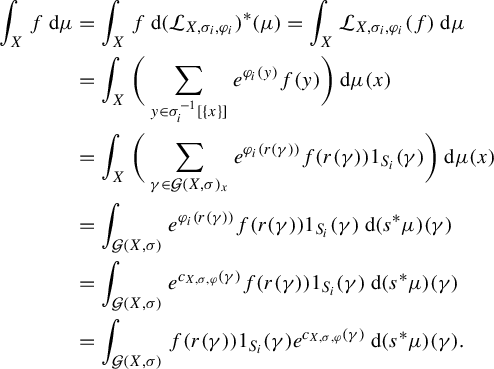$$ \begin{align*} \int_{X} f ~ \mathrm{d} \mu & = \int_{X} f ~ \mathrm{d} ({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\mu}) = \int_{X} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} ({f}) ~ \mathrm{d} \mu \\ & = \int_{X} \bigg( \sum_{y \in \sigma_{i}^{- 1} [ \{ x \} ]} e^{\varphi_{i} ({y})} f ({y}) \bigg) ~ \mathrm{d} \mu ({x}) \\ & = \int_{X} \bigg( \sum_{\gamma \in \mathcal{G} ({X,\sigma})_{x}} e^{\varphi_{i} ({r ({\gamma})})} f ({r ({\gamma})}) 1_{S_{i}} ({\gamma}) \bigg) ~ \mathrm{d} \mu ({x}) \\ & = \int_{\mathcal{G} ({X,\sigma})} e^{\varphi_{i} ({r ({\gamma})})} f ({r ({\gamma})}) 1_{S_{i}} ({\gamma}) ~ \mathrm{d} ({s^{\ast} \mu}) ({\gamma}) \\ & = \int_{\mathcal{G} ({X,\sigma})} e^{c_{X,\sigma,\varphi} ({\gamma})} f ({r ({\gamma})}) 1_{S_{i}} ({\gamma}) ~ \mathrm{d} ({s^{\ast} \mu}) ({\gamma}) \\ & = \int_{\mathcal{G} ({X,\sigma})} f ({r ({\gamma})}) 1_{S_{i}} ({\gamma}) e^{c_{X,\sigma,\varphi} ({\gamma})} ~ \mathrm{d} ({s^{\ast} \mu}) ({\gamma}). \end{align*} $$

From the above equations, it follows that the Radon–Nikodym derivative of $ r^{\ast } \mu $ with respect to $ s^{\ast } \mu $ must be equal to $ e^{c_{X,\sigma ,\varphi } ({\gamma })} $ for almost all $ \gamma \in S_{i} $ . By [22, Proposition I.3.3], $ D $ is a measurable $ \mathbb {R}\setminus \{0\} $ -valued $ 1 $ -cocycle on $ \mathcal {G} ({X,\sigma }),$ and $ D =_{\operatorname {a.e.}} e^{c_{X,\sigma ,\varphi }} $ , which is continuous by assumption. Therefore, $ e^{c_{X,\sigma ,\varphi }} $ is a continuous Radon–Nikodym cocycle associated to the quasi-invariant measure $ \mu $ and we have established $ ({2}) \Longrightarrow ({1}) $ .

We now illustrate a particular problem of existence of KMS states arising in the context of $ \mathcal {G} ({X,\sigma })$ . In the following example there are no KMS states associated to the dynamics, even though one of the associated local homeomorphisms acting on X is expansive and exact.

Example 5.4. Recall that the Cuntz algebra $ \mathcal {O}_{N} $ , where $ N \geq 2 $ , is the $ C^{\ast } $ -algebra associated to the groupoid arising from the action of the standard shift $ \sigma _{N} $ on $ X_{N} := \prod _{j \in \mathbb {N}} [ N ] $ . In [21], Olesen and Pedersen proved that for $N \geq 2$ there is exactly one KMS state for $ \mathcal {O}_{N} $ with respect to the canonical gauge action $ \alpha _{N} $ of $ \mathbb {R} $ on $ \mathcal {O}_{N} $ associated to the cocycle determined by $ \varphi _{N} = 1 $ . This KMS state arises at the inverse temperature value $ \beta = \ln ({N}) $ .

Now take $ X = X_{2} \times X_{3} $ and define $ \sigma = ({\sigma _{2},\sigma _{3}}) $ , where $ \sigma _{j} $ is the standard shift on $ X_{j} $ ; also, set $ \varphi = ({\varphi _{2},\varphi _{3}}) $ with $\varphi _{2} = 1$ and $\varphi _{3} = 1$ . Note that the shift corresponding to $ ({1,1}) \in \mathbb {N}^{2} $ is expansive and exact. Consider the automorphism group $ \alpha = \alpha _{2} \otimes \alpha _{3} $ defined on the $ C^{\ast } $ -algebra corresponding to $ ({X,\sigma ,\varphi }) $ , which is the tensor product $ \mathcal {O}_{2} \otimes \mathcal {O}_{3} $ of the $ C^{\ast } $ -algebras $ \mathcal {O}_{2}$ and $\mathcal {O}_{3} $ . Suppose that for some $ \beta \in \mathbb {R} $ , there is a state $ \omega $ on this tensor product $ C^{\ast } $ -algebra that satisfies the KMS condition for the automorphism group $ \alpha $ . Then, by the Olesen–Pedersen result, $ \omega $ restricted to the $ C^{\ast } $ -subalgebra $ \mathcal {O}_{2} \otimes \mathbb {C} \operatorname {Id}_{\mathcal {O}_{3}} $ satisfies the KMS condition for $ \alpha $ only at $ \beta = \ln ({2}) $ , whereas $ \omega $ restricted to the subalgebra $ \mathbb {C} \operatorname {Id}_{\mathcal {O}_{2}} \otimes \mathcal {O}_{3} $ satisfies the KMS condition for $ \alpha $ only at $ \beta = \ln ({3}) $ . Therefore, by the aforementioned result of Olesen and Pedersen [21], there cannot be any KMS states for the $ C^{\ast } $ -algebra $ \mathcal {O}_{2} \otimes \mathcal {O}_{3} $ associated to $ ({X,\sigma ,\varphi }) $ for the automorphism group $ \alpha = \alpha _{1} \otimes \alpha _{2} $ .

We are now in a position to introduce the generalized gauge dynamics of a $ k $ -Ruelle dynamical system, which satisfies the conditions of Definition 4.2.

Definition 5.5. (Generalized gauge dynamics)

The generalized gauge dynamics of a $ k $ -Ruelle dynamical system $ ({X,\sigma ,\varphi }) $ , which satisfies the conditions of Definition 4.2, is by definition the $ \mathbb {R} $ -dynamical system $ ({C^{\ast } ({\mathcal {G} ({X,\sigma })}),\alpha ^{X,\sigma ,\varphi }}) $ defined by

$$ \begin{align*}({\alpha^{X,\sigma,\varphi}_{t} ({f})}) ({\gamma}) := e^{i t c_{X,\sigma,\varphi} ({\gamma})} f ({\gamma}) \end{align*} $$

for all $ f \in \operatorname {C_{c}} ({\mathcal {G} ({X,\sigma })}) $ , $ \gamma \in {\mathcal {G} ({X,\sigma })} $ , and $ t \in \mathbb {R} $ , where here we are implicitly using the canonical embedding of $ \operatorname {C_{c}} ({\mathcal {G} ({X,\sigma })}) $ into $ C^{\ast }_{\textrm {r}} ({\mathcal {G} ({X,\sigma })}) $ .

The following result may be found in [22]; see also the discussion preceding Proposition 3.2 of [17].

Proposition 5.6. [22]

Let $ ({X,\sigma ,\varphi }) $ be a $ k $ -Ruelle dynamical system that satisfies the conditions of Definition 4.2 and let $ \beta \in \mathbb {R} $ . Then, for every quasi-invariant measure $ \mu $ for $ ({X,\sigma }) $ with continuous Radon–Nikodym derivative $ e^{- \beta c_{X,\sigma ,\varphi }} $ , there exists a $ \operatorname {KMS}_{\beta } $ -state $ \omega $ for the generalized gauge dynamics of $ ({X,\sigma ,\varphi }) $ that is uniquely determined by

$$ \begin{align*}\omega ({f}) = \int_{X} f ({x,0,x}) ~ \mathrm{d} \mu \end{align*} $$

for all $ f \in \operatorname {C_{c}} ({\mathcal {G} ({X,\sigma })}) $ .

It is not necessarily the case that for every $ \operatorname {KMS}_{\beta } $ -state for the generalized gauge dynamics of a $ k $ -Ruelle dynamical system, which satisfies the conditions of Definition 4.2, $ ({X,\sigma ,\varphi }) $ originates from a quasi-invariant measure for $ ({X,\sigma }) $ with $ e^{- \beta c_{X,\sigma ,\varphi }} $ as a continuous Radon–Nikodym derivative, as described above. However, Kumjian and Renault showed in [17, Proposition 3.2] that this is indeed the case if $ c_{X,\sigma ,\varphi }^{- 1} [ \{ 0 \} ] $ is a principal subgroupoid of $ \mathcal {G} ({X,\sigma }) $ .

Using Proposition 5.6, we can now prove the following result.

Theorem 5.7. Let $ ({X,\sigma ,\varphi }) $ be a k-Ruelle dynamical system, which has a unique eigenmeasure as in Definition 4.2, and $ \beta \in \mathbb {R} \setminus \{ 0 \} $ be such that $ ({\mathcal {L}_{X,\sigma _{i},\beta \varphi _{i}}})^{\ast } ({\mu }) = \mu $ for each $ i \in [ k ] $ , where $ \mu $ is an eigenmeasure for the corresponding Ruelle operator with eigenvalue one; see Definition 2.1(2). Then there exists a $ \operatorname {KMS}_{\beta } $ state as in Proposition 5.6 for the generalized gauge dynamics corresponding to $ ({X,\sigma ,\beta \varphi }) $ .

Even if the $ k $ -Ruelle dynamical system does not satisfy the conditions of Definition 4.2 so that there does not exist an eigenmeasure for the dual of the Ruelle operator with eigenvalue one, we can sometimes modify the $ 1 $ -cocycle $ \varphi $ to obtain a new $ 1 $ -cocycle $ {\varsigma } $ that does satisfy those hypotheses. The next result was motivated by [12, Proposition 4.4], which was in turn based on [18, Remark 5.25 and Proposition 5.8].

Corollary 5.8. Let $ ({X,\sigma ,\varphi }) $ be a $ k $ -Ruelle dynamical system satisfying the conditions in Definition 4.2. For $ i \in [ k ] $ and $ x \in X $ , define

$$ \begin{align*}\varsigma_{i} ({x}) := \ln ({\unicode{x3bb}^{X,\sigma,\varphi}_{i}}) - \varphi_{i} ({x}) \quad \text{and} \quad \varsigma := ({\varsigma_{i}})_{i \in [ k ]}. \end{align*} $$

Then $ ({X,\sigma ,\varsigma }) $ is a $ k $ -Ruelle dynamical system and $ \mu ^{X,\sigma ,\varsigma } $ is a quasi-invariant measure for $ ({X,\sigma }) $ with continuous Radon–Nikodym derivative $ e^{- c_{X,\sigma ,\varsigma }} $ . Moreover, $ \mu ^{X,\sigma ,\varsigma } = \mu ^{X,\sigma ,\varphi } $ , so that $ \mu ^{X,\sigma ,\varsigma } $ corresponds by Proposition 5.6 to a KMS state for the generalized gauge dynamics of $ ({X,\sigma ,\varsigma }) $ .

Proof Since the $ ({\varphi _{i}})_{i \in [ k ]} $ satisfies the cocycle condition, it is easily checked that $ ({ \varsigma _{i}})_{i \in [ k ]} = ({\ln ({\unicode{x3bb} ^{X,\sigma ,\varphi }_{i}})- \varphi _{i} })_{i \in [ k ]} $ satisfies the cocycle condition, so that $ ({X,\sigma ,\varsigma }) $ is a $ k $ -Ruelle dynamical system. Similarly, $ ({X,\sigma ,- \varsigma }) $ is a $ k $ -Ruelle dynamical system too.

Suppose that $ ({\alpha _{i}})_{i \in [ k ]} $ is a $ k $ -tuple in $ \mathbb {N}_{> 0} $ and $ \nu $ is a Borel probability measure on $ X $ such that $ ({\mathcal {L}_{X,\sigma _{i},- \varsigma _{i}}})^{\ast } ({\nu }) = \alpha _{i} \nu $ for all $ i \in [ k ] $ . Then, for each $ i \in [ k ] $ , the equalities

$$ \begin{align*}\mathcal{L}_{X,\sigma_{i},- \varsigma_{i}} = \mathcal{L}_{X,\sigma_{i},\varphi_{i} - \ln ({\unicode{x3bb}^{X,\sigma,\varphi}_{i}})} = e^{- \ln ({\unicode{x3bb}^{X,\sigma,\varphi}_{i}})} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} = \frac{1}{\unicode{x3bb}^{X,\sigma,\varphi}_{i}} \mathcal{L}_{X,\sigma_{i},\varphi_{i}} \end{align*} $$

imply that

$$ \begin{align*}({\mathcal{L}_{X,\sigma_{i},\varphi_{i}}})^{\ast} ({\nu}) = ({\unicode{x3bb}^{X,\sigma,\varphi}_{i} \mathcal{L}_{X,\sigma_{i},- \varsigma_{i}}})^{\ast} ({\nu}) = \unicode{x3bb}^{X,\sigma,\varphi}_{i} ({\mathcal{L}_{X,\sigma_{i},- \varsigma_{i}}})^{\ast} ({\nu}) = \unicode{x3bb}^{X,\sigma,\varphi}_{i} \alpha_{i} \nu. \end{align*} $$

As $ ({X,\sigma ,\varphi }) $ satisfies Definition 2.3, it follows that $ \nu = \mu ^{X,\sigma ,\varphi } $ and $ \alpha _{i} = 1 $ for each $ i \in [ k ] $ , so $ ({X,\sigma ,- \varsigma }) $ satisfies Definition 2.3 too. Moreover, by Definition 4.2, we have $ \mu ^{X,\sigma ,\varsigma } = \mu ^{X,\sigma ,\varphi } $ .

Now, as $ ({\mathcal {L}_{X,\sigma _{i},- \varsigma _{i}}})^{\ast } ({\mu ^{X,\sigma ,\varphi }}) = \mu ^{X,\sigma ,\varphi } $ for all $ i \in [ k ] $ , Theorem 5.3 tells us that $ \mu ^{X,\sigma ,\varphi } $ is quasi-invariant for $ ({X,\sigma }) $ with continuous Radon–Nikodym derivative $ e^{c_{X,\sigma ,- \varsigma }} = e^{- c_{X,\sigma ,\varsigma }} $ . Therefore, by Proposition 5.6, $ \mu ^{X,\sigma ,\varphi } $ corresponds to a KMS state for the generalized gauge dynamics of $ ({X,\sigma ,\varsigma }) $ .

The following corollary is thus clear.

Corollary 5.9. Let $ ({X,\sigma ,\varphi }) $ be a $ k $ -Ruelle dynamical system, which satisfies the conditions of Definition 4.2, and let $ \beta \in \mathbb {R}\setminus \{ 0\} $ . Define (with notation as in Definition 4.2), for $ i \in [ k ] $ and $ x \in X $ ,

$$ \begin{align*}\varsigma_{i} ({x}) := \frac{\ln ({\unicode{x3bb}^{X,\sigma,\varphi}_{i}}) - \varphi_{i} ({x})}{\beta} \quad \text{and} \quad \varsigma := ({\varsigma_{i}})_{i \in [ k ]}. \end{align*} $$

Then $ ({X,\sigma ,\varsigma }) $ also satisfies the conditions of Definition 4.2 and $ \mu ^{X,\sigma ,\varsigma } = \mu ^{X,\sigma ,\varphi } $ is a quasi-invariant measure for $ ({X,\sigma }) $ with continuous Radon–Nikodym derivative $ e^{- \beta c_{X,\sigma ,\varsigma }} $ . Consequently, $ \mu ^{X,\sigma ,\varphi } $ corresponds by Proposition 5.6 to a $ \operatorname {KMS}_{\beta } $ state for the generalized gauge dynamics of $ ({X,\sigma ,\varsigma }) $ .

6 KMS states associated to higher-rank graphs

In this section, we shall use the results obtained thus far to answer existence and uniqueness questions on KMS states for generalized gauge dynamics associated to finite higher-rank graphs.

In what follows, $ \mathbb {N}^{k} $ is viewed as a countable category with a single object $ 0 $ and composition of morphisms implemented by $ + $ .

Definition 6.1. (k-Graphs [15])

A higher-rank graph $ \Lambda $ of rank $ k $ or, more briefly, a $ k $ -graph is a countable category $ \Lambda $ equipped with a functor $ d: \Lambda \to \mathbb {N}^{k} $ —called the degree functor—such that the factorization property holds: for every $ \unicode{x3bb} \in \Lambda $ and $ m,n \in \mathbb {N}^{k} $ such that $ d ({\unicode{x3bb} }) = m + n $ , there are unique $ \mu ,\nu \in \Lambda $ that satisfy the following conditions:

1. (1) $ d ({\mu }) = m $ and $ d ({\nu }) = n $ ;

2. (2) $ \unicode{x3bb} = \mu \nu $ .

For notational convenience, we will adopt the following $ k $ -graph-theoretic terminology. Given a $ k $ -graph $ \Lambda $ with degree functor $ d $ , for each $ n \in \mathbb {N}^{k} $ , let $ \Lambda ^{n} := d^{- 1} [ \{ n \} ] $ . The elements of $ \Lambda ^{0} $ are called the vertices of $ \Lambda $ and it can be shown that $ \operatorname {Obj} ({\Lambda }) = \Lambda ^{0} $ . The elements of $ \Lambda ^{\mathbf {e}_{i}} $ , for $ \mathbf {e}_{i} $ a canonical generator of $\mathbb {N}^{k} $ , are called the edges of $ \Lambda $ . Also, let

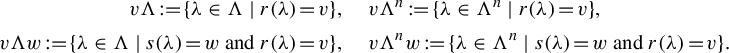$$ \begin{gather*} v \Lambda \kern1.2pt{:=}\kern1.2pt \{ \unicode{x3bb} \in \Lambda ~ | ~ r ({\unicode{x3bb}}) \kern1.2pt{=}\kern1.2pt v \}, \quad v \Lambda^{n} \kern1.2pt{:=}\kern1.2pt \{ \unicode{x3bb} \in \Lambda^{n} ~ | ~ r ({\unicode{x3bb}}) \kern1.2pt{=}\kern1.2pt v \}, \\ v \Lambda w \kern1.2pt{:=}\kern1.2pt \{ \unicode{x3bb} \in \Lambda ~ | ~ s ({\unicode{x3bb}}) \kern1.2pt{=}\kern1.2pt w ~ \text{and} ~ r ({\unicode{x3bb}}) \kern1.2pt{=}\kern1.2pt v \}, \quad v \Lambda^{n} w \kern1.2pt{:=}\kern1.2pt \{ \unicode{x3bb} \in \Lambda^{n} ~ | ~ s ({\unicode{x3bb}}) \kern1.2pt{=}\kern1.2pt w ~ \text{and} ~ r ({\unicode{x3bb}}) \kern1.2pt{=}\kern1.2pt v \}. \end{gather*} $$

A $ k $ -graph $ \Lambda $ is called finite if $ \textsf {Card} ({\Lambda ^{n}}) < \infty $ for all $ n \in \mathbb {N}^{k} $ ; $ \Lambda $ is said to be source-free if $ v \Lambda ^{n} \neq \varnothing $ for all $ n \in \mathbb {N}^{k} $ and $ v \in \Lambda ^{0} $ ; and $ \Lambda $ is said to be row-finite if $ v \Lambda ^{n}$ is finite for all $ n \in \mathbb {N}^{k} $ and $ v \in \Lambda ^{0} $ .

Moreover, a $ k $ -graph morphism from a $ k $ -graph $ \Lambda $ to another $ \Lambda ' $ is a degree-preserving functor $ f: \Lambda \to \Lambda ' $ .

Definition 6.2. (Strong connectivity and primitivity [1, 15, 16])

Let $ \Lambda $ be a $ k $ -graph. Then $ \Lambda $ is said to be strongly connected if $ v \Lambda w \neq \varnothing $ for all $ v,w \in \Lambda ^{0} $ , while $ \Lambda $ is said to be primitive if there is an $ n \in \mathbb {N}^{k} \setminus \{ 0 \} $ such that $ v \Lambda ^{n} w \neq \varnothing $ for all $ v,w \in \Lambda ^{0} $ . Evidently, primitivity is a stronger condition than strong connectivity.

Remark 6.3. Note that $ \mathbb {N}^{k} $ may itself be regarded as a $ k $ -graph with one vertex. It is called the trivial $ k $ -graph and is both finite and primitive.

Example 6.4. (See Example 1.7(ii) of [15])

Consider the countable category $ \Omega _{k} $ whose underlying set is

$$ \begin{align*}\Omega_{k} := \{ ({m,n}) \in \mathbb{N}^{k} \times \mathbb{N}^{k} ~ | ~ m \leq n \} \end{align*} $$

and whose range map, source map, and morphisms are defined as follows.

• • If $ ({m,n}) \in \Omega _{k} $ , then $ s ({m,n}) := ({n,n}) $ and $ r ({m,n}) := ({m,m}) $ , so that $ ({({k,l}),({m,n})}) \in \Omega _{k}^{2} $ is composable if and only if $ l = m $ .

• • If $ ({l,m}),({m,n}) \in \Omega _{k} $ , then $ ({l,m}) ({m,n}) := ({l,n}) $ .

If we equip $ \Omega _{k} $ with the degree functor $ d: \Omega _{k} \to \mathbb {N}^{k} $ defined by $ d ({m,n}) := n - m $ for $ ({m,n}) \in \Omega _{k} $ , then $ \Omega _{k} $ is a $ k $ -graph. Note that $ \Omega _{k} $ is both source-free and row-finite but neither finite nor strongly connected.

For the remainder of this section, we shall make the following standing assumptions:

(14) $$ \begin{align} \text{The } k \text{-graph } \Lambda \text{ is source-free, finite, primitive, and non-empty.} \end{align} $$

We will now detail more $ k $ -graph structures.

Definition 6.5. (Infinite path space [15])

Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). The infinite path space of $ \Lambda $ , denoted by $ \Lambda ^{\infty } $ , is defined by

$$ \begin{align*}\Lambda^{\infty} := \{ f: \Omega_{k} \to \Lambda ~ | ~ f ~ \text{is a} ~ k \text{-graph morphism} \}. \end{align*} $$

As $ \Lambda $ is source-free and finite, $ \Lambda ^{\infty } $ becomes a non-empty compact Hausdorff space when given the topology generated by the base consisting of cylinder sets, that is, non-empty compact subsets of the form $ \mathcal {Z} ({\unicode{x3bb} }) $ for all $ \unicode{x3bb} \in \Lambda $ , where

$$ \begin{align*}\mathcal{Z} ({\unicode{x3bb}}) := \{ x \in \Lambda^{\infty} ~ | ~ x ({0,d ({\unicode{x3bb}})}) = \unicode{x3bb} \}. \end{align*} $$

We can then define a commuting $ k $ -tuple $ \sigma = ({\sigma _{i}})_{i \in [ k ]} $ of local homeomorphisms of $ \Lambda ^{\infty } $ by setting, for all $ i \in [ k ] $ , $ x \in \Lambda ^{\infty } $ , and $ ({m,n}) \in \Omega _{k} $ ,

$$ \begin{align*}[ \sigma_{i} ({x}) ] ({m,n}) := x ({m + \mathbf{e}_{i},n + \mathbf{e}_{i}}). \end{align*} $$

We call the $ k $ -tuple $ \sigma $ the shift on $ \Lambda $ and it is easy to see that, for all $ l \in \mathbb {N}^{k} $ , $ x \in \Lambda ^{\infty } $ , and $ ({m,n}) \in \Omega _{k} $ ,

$$ \begin{align*}[ \sigma^{l} ({x}) ] ({m,n}) = x ({m + l,n + l}). \end{align*} $$

Furthermore, it can be shown that $ \sigma _{i} $ is surjective for each $ i \in [ k ] $ . We refer the reader to [15] for details.

We now state the following lemma, whose standard proof we omit; see, for example, [11, Proposition 2.15].

Lemma 6.6. Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). Define $ \rho _{\Lambda }: \Lambda ^{\infty } \times \Lambda ^{\infty } \to \mathbb {R}_{\geq 0} $ , where, for all $ x,y \in \Lambda ^{\infty } $ , we set $ \rho _{\Lambda } ({x,y}) : = {2^{- N_{x y}}} $ with

$$ \begin{align*}N_{x y} := \min ({\{ n \in \mathbb{N} ~ | ~ x ({n p,({n + 1}) p}) \neq y ({n p,({n + 1}) p}) \}}). \end{align*} $$

Here, we have arbitrarily chosen $ p \in \mathbb {N}^{k} $ to satisfy $ ({1})_{i \in [ k ]} \leq p $ . Furthermore, $ \min ({\varnothing }) := \infty $ by convention. Then $ \rho _{\Lambda } $ is a metric on $ \Lambda ^{\infty } $ compatible with the cylinder set topology.

Lemma 6.7. Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). For any $ p \in N^{k} $ satisfying $ ({1})_{i \in [ k ]} \leq p $ , the local homeomorphism $ \sigma ^{p} $ is positively expansive and exact.

Proof If $ x,y \in \Lambda ^{\infty } $ are distinct, then $ x ({n p,({n + 1}) p}) \neq y ({n p,({n + 1}) p}) $ for some $ n \in \mathbb {N} $ . From this, one easily verifies that $ \rho _{\Lambda } ({({\sigma ^{p}})^{n } ({x}),({\sigma ^{p}})^{n} ({y})}) = 1 $ . Hence, $ \sigma ^{p} $ is positively expansive.

To prove exactness, for fixed $ \unicode{x3bb} \in \Lambda $ , we will show that $ \sigma ^{n p} [ \mathcal {Z} ({\unicode{x3bb} }) ] = \Lambda ^{\infty } $ for some $ n \in \mathbb {N} $ . For, as $ \Lambda $ is primitive, there exists $ q \in \mathbb {N}^{k} \setminus \{ 0 \} $ such that $ v \Lambda ^{q} w \neq \varnothing $ for all $ v,w \in \Lambda ^{0} $ . Now choose $ n \in \mathbb {N} $ such that $ d ({\unicode{x3bb} }) + q \leq n p $ and $ y \in \Lambda ^{\infty } $ . As $ \Lambda $ is source-free, there exists $ \mu \in s ({\unicode{x3bb} }) \Lambda ^{n p - d ({\unicode{x3bb} }) - q} $ . Next, for any $ \nu \in s ({\mu }) \Lambda ^{q} y ({0,0}) $ , $ ({\unicode{x3bb} ,\mu ,\nu }) $ forms a composable triple. Since $ y ({0,0}) = s ({\unicode{x3bb} \mu \nu }) $ , Proposition 2.3 of [15] implies that there exists $ x \in \Lambda ^{\infty } $ such that $ y = \sigma ^{d ({\unicode{x3bb} \mu \nu })} ({x}) = \sigma ^{n p} ({x}) $ with

$$ \begin{align*}\unicode{x3bb} \mu \nu = x ({0,n p}) = x ({0,d ({\unicode{x3bb}})}) ~ x ({d ({\unicode{x3bb}}),n p - q}) ~ x ({n p - q,n p}). \end{align*} $$

By the factorization property, we get $ x ({0,d ({\unicode{x3bb} })}) = \unicode{x3bb} $ , so $ x \in \mathcal {Z} ({\unicode{x3bb} }) $ . Hence, $ y \in \sigma ^{n p} [ \mathcal {Z} ({\unicode{x3bb} }) ] $ and, since $ y \in \Lambda ^{\infty } $ is arbitrary, we obtain $ \sigma ^{n p} [ \mathcal {Z} ({\unicode{x3bb} }) ] = \Lambda ^{\infty } $ . Therefore, $ \sigma ^{n p} $ is exact.

As for Ruelle dynamical systems, there is a version of the RPF theorem for $ k $ -graphs.

Theorem 6.8. Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). Assume that $ \varphi = ({\varphi _{i}})_{i \in [ k ]} $ is a $ k $ -tuple of continuous real-valued functions on $ \Lambda ^{\infty } $ satisfying the cocycle condition and let $ c_{\varphi } $ denote the associated $ 1 $ -cocycle. If there exists a $ p \in \mathbb {N}^{k} $ with $ ({1})_{i \in [ k ]} \leq p $ such that $ c_{\varphi } ({p}): \Lambda ^\infty \to \mathbb {R} $ is Hölder-continuous with respect to $ \rho _{\Lambda } $ , then the triple $ ({\Lambda ^{\infty },\sigma ,\varphi }) $ satisfies the conditions in Definition 4.2.

Proof By Lemma 6.6, and Lemma 6.7, the Ruelle triple $(\Lambda^\infty, \sigma^p, c_\varphi(p))$ satisfies the conditions in Definition 2.5, so, by Theorems 2.7 and 4.3, the result follows.

Note that Proposition 4.3, Theorem 2.4 and Theorem 6.8 will guarantee the existence of a Borel measure $ \mu ^{\varphi } $ on $ \Lambda ^{\infty } $ . We will now establish some useful properties of this measure.

Proposition 6.9. Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). Suppose that $ ({\Lambda ^{\infty },\sigma ,\varphi }) $ with $ \varphi = ({\varphi _{i}})_{i \in [ k ]} $ a $ k $ -tuple of continuous real-valued functions on $ \Lambda ^{\infty } $ satisfying the cocycle condition. Let $ c_{\varphi } $ denote the associated $ 1 $ -cocycle. If $ ({\Lambda ^{\infty },\sigma ,\varphi }) $ is a $ k $ -Ruelle dynamical system satisfying the conditions in Definition 4.2, then, for all $ \unicode{x3bb} \in \Lambda $ ,

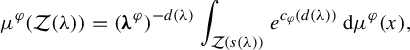$$ \begin{align*}\mu^{\varphi} ({\mathcal{Z} ({\unicode{x3bb}})}) = ({\boldsymbol{\unicode{x3bb}}^{\varphi}})^{- d ({\unicode{x3bb}})} \int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} e^{c_{\varphi} ({d ({\unicode{x3bb}})})} ~ \mathrm{d} \mu^{\varphi}{(x)}, \end{align*} $$

where to simplify the notation we denote by $ \boldsymbol {\unicode{x3bb} }^{\varphi } $ (respectively $\mu ^\varphi $ ) the $ k $ -tuple of eigenvalues (respectively the eigenmeasure) associated to the k-Ruelle dynamical system $ ({\Lambda ^{\infty },\sigma ,\varphi }) $ .

Proof Fix an arbitrary $ \unicode{x3bb} \in \Lambda $ . For every $ i \in [ k ] $ , we have $ ({\mathcal {L}_{\Lambda ^{\infty },\sigma _{i},\varphi _{i}}})^{\ast } ({\mu ^{\varphi }}) = \unicode{x3bb} ^{\varphi }_{i} \mu ^{\varphi } $ . Hence,

$$ \begin{align*}({\mathcal{L}_{\Lambda^{\infty},\sigma^{d ({\unicode{x3bb}})},c_{\varphi} ({d ({\unicode{x3bb}})})}})^{\ast} ({\mu^{\varphi}}) = ({\boldsymbol{\unicode{x3bb}}^{\varphi}})^{d ({\unicode{x3bb}})} \mu^{\varphi}, \end{align*} $$

so, integrating $ 1_{\mathcal {Z} ({\unicode{x3bb} })} \in \operatorname {C} ({\Lambda ^{\infty },\mathbb {R}}) $ with respect to the equal measures on the left- and right-hand sides of the above equation and using the definition of $ ({\mathcal {L}_{\Lambda ^{\infty },\sigma ^{d ({\unicode{x3bb} })},c_{\varphi } ({d ({\unicode{x3bb} })})}})^{\ast } $ yields

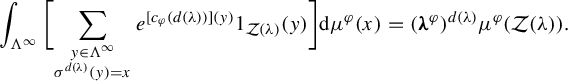$$ \begin{align*}\int_{\Lambda^{\infty}} {\bigg[{\sum_{\substack{y \in \Lambda^{\infty} \\ \sigma^{d ({\unicode{x3bb}})} ({y}) = x}} e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({y})} 1_{\mathcal{Z} ({\unicode{x3bb}})} ({y})}\bigg]} \mathrm{d} {\mu^{\varphi}}{(x)} = ({\boldsymbol{\unicode{x3bb}}^{\varphi}})^{d ({\unicode{x3bb}})} \mu^{\varphi} ({\mathcal{Z} ({\unicode{x3bb}})}). \end{align*} $$

If $ x \in \Lambda ^{\infty } \setminus \mathcal {Z} ({s ({\unicode{x3bb} })}) $ , then there does not exist a $ y \in \mathcal {Z} ({\unicode{x3bb} }) $ such that $ \sigma ^{d ({\unicode{x3bb} })} ({y}) = x $ , so

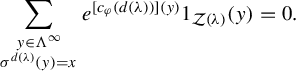$$ \begin{align*}\sum_{\substack{y \in \Lambda^{\infty} \\ \sigma^{d ({\unicode{x3bb}})} ({y}) = x}} e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({y})} 1_{\mathcal{Z} ({\unicode{x3bb}})} ({y}) = 0. \end{align*} $$

It follows that

$$ \begin{align*} &\int_{\Lambda^{\infty}} ~ {\bigg[{\sum_{\substack{y \in \Lambda^{\infty} \\ \sigma^{d ({\unicode{x3bb}})} ({y}) = x}} e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({y})} 1_{\mathcal{Z} ({\unicode{x3bb}})} ({y})}\bigg]} \mathrm{d} {\mu^{\varphi}}({x})\\ &\quad= \int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} ~ {\bigg[{\sum_{\substack{y \in \Lambda^{\infty} \\ \sigma^{d ({\unicode{x3bb}})} ({y}) = x}} e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({y})} 1_{\mathcal{Z} ({\unicode{x3bb}})} ({y})}\bigg]} \mathrm{d} {\mu^{\varphi}}({x }). \end{align*} $$

Given an $ x \in \mathcal {Z} ({s ({\unicode{x3bb} })}) $ , there exists precisely one $ y \in \mathcal {Z} ({\unicode{x3bb} }) $ such that $ \sigma ^{d ({\unicode{x3bb} })} ({y}) = x $ , namely, $ \unicode{x3bb} x $ . Consequently,

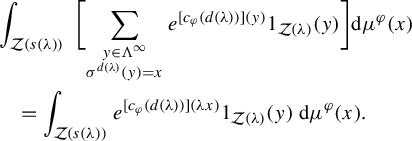$$ \begin{align*} &\int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} ~ {\bigg[{\sum_{\substack{y \in \Lambda^{\infty}\\ \sigma^{d ({\unicode{x3bb}})} ({y}) = x}}e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({y})} 1_{\mathcal{Z} ({\unicode{x3bb}})} ({y})}\bigg]} \mathrm{d} {\mu^{\varphi}}({x})\\ &\quad= \int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({\unicode{x3bb} x})} 1_{\mathcal{Z} ({\unicode{x3bb}})} ({y}) ~ \mathrm{d} \mu^{\varphi} ({x}). \end{align*} $$

Therefore,

$$ \begin{align*}\int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} e^{[ c_{\varphi} ({d ({\unicode{x3bb}})}) ] ({\unicode{x3bb} x})} ~ \mathrm{d} \mu^{\varphi} ({x}) = ({\boldsymbol{\unicode{x3bb}}^{\varphi}})^{d ({\unicode{x3bb}})} \mu^{\varphi} ({\mathcal{Z} ({\unicode{x3bb}})}) \end{align*} $$

and a simple rearrangement of terms yields the proposition.

We list an important positivity property of the measure $ \mu ^{\varphi } $ in the event that $ ({\Lambda ^{\infty },\sigma ,\varphi }) $ satisfies the conditions in Definition 4.2.

Corollary 6.10. Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). Suppose that $ ({\Lambda ^{\infty },\sigma ,\varphi }) $ is a $ k $ -Ruelle dynamical system that satisfies the conditions of Definition 4.2. Then $ \mu ^{\varphi } ({\mathcal {Z} ({\unicode{x3bb} })})> 0 $ for every $ \unicode{x3bb} \in \Lambda $ .

Proof Suppose by way of contradiction that there exists $ \unicode{x3bb} \in \Lambda $ such that $ \mu ^{\varphi } ({\mathcal {Z} ({\unicode{x3bb} })}) = 0 $ . By Lemma 6.7, if $ ({1})_{i \in [ k ]} \leq p $ , then $ \sigma ^{p} $ is positively expansive and exact. But then there exists $ n \in \mathbb {N} $ such that $ \sigma ^{n p} [ \mathcal {Z} ({\unicode{x3bb} }) ] = \Lambda ^{\infty } $ . We now use Proposition 4.2 of [24] again to deduce that

$$ \begin{align*}\mu^{\varphi} ({\Lambda^{\infty}}) = \mu^{\varphi} ({\sigma^{n p} [ \mathcal{Z} ({\unicode{x3bb}}) ]}) = \mu^{\varphi} ({\mathcal{Z} ({\unicode{x3bb}})}) = 0. \end{align*} $$

Since $ \mu ^{\varphi } ({\Lambda ^{\infty }}) = 1 $ , this gives us a contradiction.

Recall that if $ \Lambda $ is a $ k $ -graph and $ H $ is an abelian group, a map $ h: \Lambda \to H $ is called a categorical $ 1 $ -cocycle if $ h ({\unicode{x3bb} \mu }) = h ({\unicode{x3bb} }) + h ({\mu }) $ whenever $ ({\unicode{x3bb} ,\mu }) $ is composable. In the case when $ H = \mathbb {R} $ and the image of $ h $ lies entirely inside the non-negative real numbers, $ h $ was called an ‘ $ \mathbb {R}^{+} $ -functor’ in [12].

Next, observe that, if $ h $ is a categorical $ 1 $ -cocycle taking values in $ \mathbb {R} $ , then a routine calculation shows that the $ k $ -tuple of functions $ \varphi ^{h,\theta } := ({\varphi ^{h,\theta }_{i}})_{i \in [ k ]} $ , where $ \varphi ^{h,\theta }_{i}: \Lambda ^{\infty } \to \mathbb {R} $ is defined for all $ i \in [ k ] $ and $ x \in \Lambda ^{\infty } $ by

(15) $$ \begin{align} \varphi^{h,\theta}_{i} ({x}) = - \theta h ({x ({0,\mathbf{e}_{i}})}), \end{align} $$

satisfies the cocycle condition and therefore determines a groupoid $ 1 $ -cocycle on $ \mathcal {G} ({\Lambda ^{\infty },\sigma }) $ taking values in $ \mathbb {R} $ by Lemma 3.12; we will call this cocycle $ c_{\varphi ^{h,\theta }} $ . Hence, $ ({\Lambda ^{\infty },\sigma ,c_{\varphi ^{h,\theta }}}) $ is a $ k $ -Ruelle dynamical system.

Example 5.4 has shown that an automorphism group on a $ C^{\ast } $ -algebra coming from $ ({X,\sigma ,\varphi }) $ need not have a KMS state. However, by using Corollary 5.8 and other results, we can construct a new cocycle from $ \varphi $ giving rise to a different dynamics for which a KMS state does exist. The following theorem was first proved in a different way in Proposition 4.4 in [12].

Theorem 6.11. [12]

Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14). Let $ h: \Lambda \to \mathbb {R} $ be a non-negative categorical $ 1 $ -cocycle and let $ \theta $ be a positive real number. Let $ \varphi ^{h,\theta } = ({\varphi ^{h,\theta }_i})_{i \in [ k ]} $ be as defined in equation (15). Then $ ({\Lambda ^{\infty },\sigma ,\varphi ^{h,\theta }}) $ is a $ k $ -Ruelle dynamical system that satisfies the conditions in Definition 4.2 and, for each $ \beta \in \mathbb {R}\setminus \{0\} $ , so does

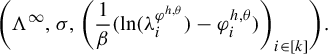$$ \begin{align*}\bigg({\Lambda^{\infty}},{\sigma},{\bigg({\frac{1}{\beta} ({\ln ({\unicode{x3bb}^{\varphi^{h,\theta}}_{i}}) - \varphi^{h,\theta}_{i}})}\bigg)_{i \in [ k ]}}\bigg). \end{align*} $$

The associated generalized state $ \omega $ on $ C^{\ast }_{\textrm {r}} ({\mathcal {G} ({\Lambda ^{\infty },\sigma })}) \cong C^{\ast } ({\Lambda }) $ uniquely determined by

$$ \begin{align*}\text{ for all } f \in \operatorname{C_{c}} ({\mathcal{G} ({\Lambda^{\infty},\sigma})}): \omega ({f}) = \int_{\Lambda^{\infty}} f ({x,0,x}) ~ \mathrm{d} \mu^{\varphi^{h,\theta}}(x) \end{align*} $$

is a $ \operatorname {KMS}_{\beta } $ state for the dynamics determined by the cocycle $ \varsigma $ given by

$$ \begin{align*}\varsigma := \bigg({\frac{1}{\beta} ({\ln ({\unicode{x3bb}^{\varphi^{h,\theta}}_{i}}) - \varphi^{h,\theta}_{i}})}\bigg)_{i \in [ k ]}; \end{align*} $$

moreover, $ \mu ^{\varsigma } = \mu ^{\varphi ^{h,\theta }} $ .

Proof Fix an arbitrary $ n \in \mathbb {N}^{k} $ . We will first prove that the function $ f: \Lambda ^{\infty } \to \mathbb {R} $ defined by, for all $x \in \Lambda ^{\infty }$ ,

$$ \begin{align*}f ({x}) := h ({x ({0,n})}) \end{align*} $$

is Hölder-continuous with respect to $ \rho _{\Lambda } $ . As $ \Lambda ^{n} $ is finite, $ h $ clearly achieves both a minimum value $ m $ and a maximum value $ M $ on $ \Lambda ^{n} $ . Choose $ N \in \mathbb {N} $ such that $ n \leq N p $ with $ ({1})_{i \in [ k ]} \leq p $ . For $ x,y \in \Lambda ^{\infty } $ such that $ \rho _{\Lambda } ({x,y}) < {1}/{2^{N}} $ , for all $ j \in [ N ] $ ,

$$ \begin{align*}x ({j p,({j + 1}) p}) = y ({j p,({j + 1}) p}), \end{align*} $$

so $ x ({0,N p}) = y ({0,N p}) $ , which yields $ x ({0,n}) = y ({0,n}) $ by the factorization property. Consequently, for all $x,y \in \Lambda ^{\infty }$ ,

$$ \begin{align*}\lvert f ({x}) - f ({y}) \rvert = \lvert h ({x ({0,n})}) - h ({y ({0,n})}) \rvert \leq N ({M - m}) \rho_{\Lambda} ({x,y}). \end{align*} $$

As $ n \in \mathbb {N}^{k} $ is arbitrary, it follows that $ \varphi ^{h,\theta }_{i} $ is Hölder-continuous with respect to $ \rho _{\Lambda } $ for each $ i \in [ k ] $ .

A straightforward calculation demonstrates that $ c_{\varphi ^{h,\theta }} ({p}) $ is Hölder-continuous with respect to $ \rho _{\Lambda } $ ; therefore, by applying Theorem 6.8, we conclude that $ ({\Lambda ^{\infty },\sigma ,\varphi ^{h,\theta }}) $ satisfies the conditions in Definition 4.2.

Applying Theorem 6.8, we conclude that $ ({\Lambda ^{\infty },\sigma ,\varphi ^{h,\theta }}) $ satisfies the conditions in Definition 4.2.

It now follows from Corollary 5.8 that

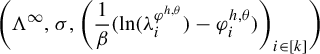$$ \begin{align*}\bigg({\Lambda^{\infty}},{\sigma},{\bigg({\frac{1}{\beta} ({\ln ({\unicode{x3bb}^{\varphi^{h,\theta}}_{i}}) - \varphi^{h,\theta}_{i}})}\bigg)_{i \in [ k ]}}\bigg) \end{align*} $$

also satisfies the conditions in Definition 4.2, with $ \mu ^{\varsigma } = \mu ^{\varphi ^{h,\theta }}$ , by Corollary 5.8. By Proposition 5.6, the state $ \omega $ on $ C^{\ast } ({\mathcal {G} ({\Lambda ^{\infty },\sigma })}) \cong C^{\ast } ({\Lambda }) $ that is uniquely determined by, for all $f \in \operatorname {C_{c}} ({\mathcal {G} ({\Lambda ^{\infty },\sigma })})$ ,

$$ \begin{align*}\omega ({f}) = \int_{\Lambda^{\infty}} f ({x,0,x}) ~ \mathrm{d} \mu^{\varphi^{h,\theta}}(x), \end{align*} $$

with notation as in Proposition 6.9, is a $ \operatorname {KMS}_{\beta } $ state for the generalized gauge dynamics of this particular dynamical system.

The following corollary gives more information about the eigenmeasure $ \mu ^{\varphi ^{h,\theta }} $ and relates it to the eigenvalues of the Ruelle–Perron–Frobenius operator.

Corollary 6.12. Let $ \Lambda $ be a $ k $ -graph satisfying the standing assumptions of (14) and let $ h: \Lambda \to \mathbb {R}_{\geq 0} $ , $ \theta \in \mathbb {R} \setminus \{0\} $ , and $ \varphi ^{h,\theta } $ be as in Theorem 6.11; let $ c_{\varphi ^{h,\theta }} $ denote the associated cocycle. Then, for all $ \unicode{x3bb} \in \Lambda $ ,

$$ \begin{align*}\mu^{\varphi^{h,\theta}} ({\mathcal{Z} ({\unicode{x3bb}})}) = ({\boldsymbol{\unicode{x3bb}}^{\varphi^{h,\theta}}})^{- d ({\unicode{x3bb}})} e^{- \theta h ({\unicode{x3bb}})} \mu^{\varphi^{h,\theta}} ({\mathcal{Z} ({s ({\unicode{x3bb}})})}), \end{align*} $$

where $ \varphi ^{h,\theta } $ is the $ k $ -tuple of elements of $ \operatorname {C} ({\Lambda ^{\infty },\mathbb {R}}) $ that is defined for all $ i \in [ k ] $ and $ x \in \Lambda ^{\infty } $ by

$$ \begin{align*}\varphi^{h,\theta}_{i} ({x}) := - \theta h ({x ({0,\mathbf{e}_{i}})}). \end{align*} $$

Proof We already know from Theorem 7.9 that for all $ n \in \mathbb {N}^{k} $ and $ x \in \Lambda ^{\infty } $ ,

$$ \begin{align*}c_{\varphi^{h,\theta}} ({n}) = - \theta h ({x ({0,n})}). \end{align*} $$

Hence, for every $ \unicode{x3bb} \in \Lambda $ , if $ x \in \mathcal {Z} ({s ({\unicode{x3bb} })}) $ , we have

$$ \begin{align*}[ c_{\varphi^{h,\theta}} ({d ({\unicode{x3bb}})}) ] ({\unicode{x3bb} x}) = - \theta h ({({\unicode{x3bb} x}) ({0,d ({\unicode{x3bb}})})}) = - \theta h ({\unicode{x3bb}}). \end{align*} $$

Consequently, by Proposition 6.9, for all $ \unicode{x3bb} \in \Lambda $ ,

$$ \begin{align*} \mu^{\varphi^{h,\theta}} ({\mathcal{Z} ({\unicode{x3bb}})}) & = ({\boldsymbol{\unicode{x3bb}}^{\varphi^{h,\theta}}})^{- d ({\unicode{x3bb}})} \int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} e^{[ c_{\varphi^{h,\theta}} ({d ({\unicode{x3bb}})}) ] ({\unicode{x3bb} x})} ~ \mathrm{d} \mu^{\varphi^{h,\theta}} ({x}) \\ & = ({\boldsymbol{\unicode{x3bb}}^{\varphi^{h,\theta}}})^{- d ({\unicode{x3bb}})} \int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} e^{- \theta h ({\unicode{x3bb}})} ~ \mathrm{d} \mu^{\varphi^{h,\theta}} ({x}) \\ & = ({\boldsymbol{\unicode{x3bb}}^{\varphi^{h,\theta}}})^{- d ({\unicode{x3bb}})} e^{- \theta h ({\unicode{x3bb}})} \int_{\mathcal{Z} ({s ({\unicode{x3bb}})})} 1 ~ \mathrm{d} \mu^{\varphi^{h,\theta}} ({x}) \\ & = ({\boldsymbol{\unicode{x3bb}}^{\varphi^{h,\theta}}})^{- d ({\unicode{x3bb}})} e^{- \theta h ({\unicode{x3bb}})} \mu^{\varphi^{h,\theta}} ({\mathcal{Z} ({s ({\unicode{x3bb}})})}). \end{align*} $$

The corollary is therefore proven.