No CrossRef data available.
Article contents
Conditional intermediate entropy and Birkhoff average properties of hyperbolic flows
Published online by Cambridge University Press: 14 November 2023
Abstract
Katok [Lyapunov exponents, entropy and periodic points of diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173] conjectured that every 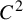 $C^{2}$ diffeomorphism f on a Riemannian manifold has the intermediate entropy property, that is, for any constant
$C^{2}$ diffeomorphism f on a Riemannian manifold has the intermediate entropy property, that is, for any constant  $c \in [0, h_{\mathrm {top}}(f))$, there exists an ergodic measure
$c \in [0, h_{\mathrm {top}}(f))$, there exists an ergodic measure 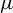 $\mu $ of f satisfying
$\mu $ of f satisfying 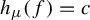 $h_{\mu }(f)=c$. In this paper, we obtain a conditional intermediate metric entropy property and two conditional intermediate Birkhoff average properties for basic sets of flows that characterize the refined roles of ergodic measures in the invariant ones. In this process, we establish a ‘multi-horseshoe’ entropy-dense property and use it to get the goal combined with conditional variational principles. We also obtain the same result for singular hyperbolic attractors.
$h_{\mu }(f)=c$. In this paper, we obtain a conditional intermediate metric entropy property and two conditional intermediate Birkhoff average properties for basic sets of flows that characterize the refined roles of ergodic measures in the invariant ones. In this process, we establish a ‘multi-horseshoe’ entropy-dense property and use it to get the goal combined with conditional variational principles. We also obtain the same result for singular hyperbolic attractors.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press


