Article contents
Conditioned limit theorems for hyperbolic dynamical systems
Published online by Cambridge University Press: 20 March 2023
Abstract
Let 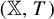 $({\mathbb X}, T)$ be a subshift of finite type equipped with the Gibbs measure
$({\mathbb X}, T)$ be a subshift of finite type equipped with the Gibbs measure 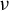 $\nu $ and let f be a real-valued Hölder continuous function on
$\nu $ and let f be a real-valued Hölder continuous function on 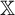 ${\mathbb X}$ such that
${\mathbb X}$ such that 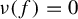 $\nu (f) = 0$. Consider the Birkhoff sums
$\nu (f) = 0$. Consider the Birkhoff sums 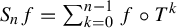 $S_n f = \sum _{k=0}^{n-1} f \circ T^{k}$,
$S_n f = \sum _{k=0}^{n-1} f \circ T^{k}$, 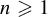 $n\geqslant 1$. For any
$n\geqslant 1$. For any 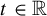 $t \in {\mathbb R}$, denote by
$t \in {\mathbb R}$, denote by 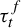 $\tau _t^f$ the first time when the sum
$\tau _t^f$ the first time when the sum 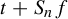 $t+ S_n f$ leaves the positive half-line for some
$t+ S_n f$ leaves the positive half-line for some 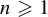 $n\geqslant 1$. By analogy with the case of random walks with independent and identically distributed increments, we study the asymptotic as
$n\geqslant 1$. By analogy with the case of random walks with independent and identically distributed increments, we study the asymptotic as 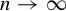 $ n\to \infty $ of the probabilities
$ n\to \infty $ of the probabilities 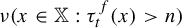 $ \nu (x\in {\mathbb X}: \tau _t^f(x)>n) $ and
$ \nu (x\in {\mathbb X}: \tau _t^f(x)>n) $ and 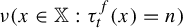 $ {\nu (x\in {\mathbb X}: \tau _t^f(x)=n) }$. We also establish integral and local-type limit theorems for the sum
$ {\nu (x\in {\mathbb X}: \tau _t^f(x)=n) }$. We also establish integral and local-type limit theorems for the sum 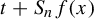 $t+ S_n f(x)$ conditioned on the set
$t+ S_n f(x)$ conditioned on the set 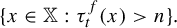 $\{ x \in {\mathbb X}: \tau _t^f(x)>n \}.$
$\{ x \in {\mathbb X}: \tau _t^f(x)>n \}.$
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by


