Article contents
The Connes spectrum for actions of Abelian groups on continuous-trace algebras
Published online by Cambridge University Press: 19 September 2008
Abstract
We study the various notions of spectrum for an action α of a locally compact abelian group G on a type IC*-algebra A, and discuss how these are related to the structure of the crossed product A ⋊αG. In the case where A has continuous trace and the action of G on  is minimal, we completely describe the ideal structure of the crossed product. A key role is played by the restriction of α to a certain ‘symmetrizer subgroup’ S of the common stabilizer in G of the points of Â. We show by example that, contrary to a conjecture of Bratteli, it is possble for A⋊G to be primitive but not simple, provided that S is not discrete. In such cases, the Connes spectrum Γ(α) differs from the strong Connes spectrum 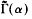 of Kishimoto. The counterexamples come from subtle phenomena in topological dynamics.
of Kishimoto. The counterexamples come from subtle phenomena in topological dynamics.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1986
References
REFERENCES
- 9
- Cited by

