Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T05:26:28.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuation and bifurcation associated to the dynamical spectral sequence

Published online by Cambridge University Press:  05 July 2013

R. FRANZOSA ,
K. A. DE REZENDE  and
M. R. DA SILVEIRA
R. FRANZOSA
Affiliation:
Department of Mathematics and Statistics, University of Maine, Orono, Maine, USA email robert_franzosa@umit.maine.edu
K. A. DE REZENDE
Affiliation:
Instituto de Matemática, Estatística e Computação Científica, Universidade Estadual de Campinas, Campinas, SP, Brazil email ketty@ime.unicamp.br
M. R. DA SILVEIRA
Affiliation:
Centro de Matemática, Computação e Cognição, Universidade Federal do ABC, Santo André, SP, Brazil email mariana.silveira@ufabc.edu.br
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider a filtered chain complex 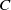$C$ and its differential given by a connection matrix 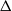$\Delta $ which determines an associated spectral sequence 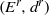$({E}^{r} , {d}^{r} )$. We present an algorithm which sweeps the connection matrix in order to span the modules 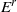${E}^{r} $ in terms of bases of 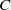$C$ and gives the differentials 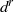${d}^{r} $. In this process a sequence of similar connection matrices and associated transition matrices are produced. This algebraic procedure can be viewed as a continuation, where the transition matrices give information about the bifurcation behavior. We introduce directed graphs, called flow and bifurcation schematics, that depict bifurcations that could occur if the sequence of connection matrices and transition matrices were realized in a continuation of a Morse decomposition, and we present a dynamic interpretation theorem that provides conditions on a parameterized family of flows under which such a continuation could occur.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 6 , December 2014 , pp. 1849 - 1887
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Conley, C.. Isolated Invariant Sets and the Morse Index (CBMS Regional Conference Series in Mathematics, 38). American Mathematical Society, Providence, RI, 1978.Google Scholar
Cornea, O., de Rezende, K. A. and da Silveira, M. R.. Spectral sequences in Conley’s theory. Ergod. Th. & Dynam. Sys. 30 (2010), 1009–1054.CrossRefGoogle Scholar
Franzosa, R.. The continuation theory for Morse decompositions and connection matrices. Trans. Amer. Math. Soc. 310 (1988), 781–803.CrossRefGoogle Scholar
Franzosa, R.. The connection matrix theory for Morse decompositions. Trans. Amer. Math. Soc. 311 (1989), 561–592.Google Scholar
Franzosa, R. and Mischaikow, K.. Algebraic transition matrices in the Conley index theory. Trans. Amer. Math. Soc. 350 (1998), 889–912.Google Scholar
McCord, C. K. and Mischaikow, K.. Connected simple systems, transition matrices and the heteroclinic bifurcations. Trans. Amer. Math. Soc. 333 (1) (1992), 397–422.Google Scholar
McCord, C. K. and Mischaikow, K.. Equivalence of topological and singular transition matrices in the Conley index theory. Michigan Math. J. 42 (2) (1995), 387–414.Google Scholar
Mello, M., de Rezende, K. A. and da Silveira, M. R.. Conley’s spectral sequences via the sweeping algorithm. Topology Appl. 157 (2010), 2111–2130.Google Scholar
Reineck, J. F.. Connecting orbits in one-parameter families of flows. Ergod. Th. & Dynam. Sys. (1988), 359–374, Charles Conley Memorial Issue.Google Scholar
Reineck, J. F.. The connection matrix in Morse-Smale flows. Trans. Amer. Math. Soc. 322 (1990), 523–545.CrossRefGoogle Scholar
Reineck, J. F.. The connection matrix in Morse-Smale flows II. Trans. Amer. Math. Soc. 347 (1995), 2097–2110.Google Scholar
Spanier, E.. Algebraic Topology. McGraw-Hill, New York, 1966.Google Scholar