Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T13:07:07.122Z Has data issue: false hasContentIssue false
  • English
  • Français

Continued fractions, the Chen–Stein method and extreme value theory

Part of: Stochastic processes Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  06 September 2019

ANISH GHOSH ,
MAXIM SØLUND KIRSEBOM  and
PARTHANIL ROY
ANISH GHOSH
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Mumbai400005, India email ghosh.anish@gmail.com
MAXIM SØLUND KIRSEBOM
Affiliation:
Department of Mathematics, University of Hamburg, 20146Hamburg, Germany email maximkirsebom@gmail.com
PARTHANIL ROY
Affiliation:
Theoretical Statistics and Mathematics Unit, Indian Statistical Institute, Bangalore560059, India email parthanil.roy@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we deal with extreme value theory in the context of continued fractions using techniques from probability theory, ergodic theory and real analysis. We give an upper bound for the rate of convergence in the Doeblin–Iosifescu asymptotics for the exceedances of digits obtained from the regular continued fraction expansion of a number chosen randomly from 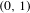$(0,1)$ according to the Gauss measure. As a consequence, we significantly improve the best known upper bound on the rate of convergence of the maxima in this case. We observe that the asymptotics of order statistics and the extremal point process can also be investigated using our methods.

Keywords

continued fractionsChen–Stein methodPoisson approximationrate of convergenceextreme value theory

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 11K50: Metric theory of continued fractions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 461 - 470
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Arratia, R., Goldstein, L. and Gordon, L.. Two moments suffice for Poisson approximations: the Chen–Stein method. Ann. Probab. 17 (1989), 9–25.CrossRefGoogle Scholar
Chang, Y. and Ma, J.. Some distribution results of the Oppenheim continued fractions. Monatsh. Math. 184(3) (2017), 379–399.CrossRefGoogle Scholar
Chiarini, A., Cipriani, A. and Hazra, R. S.. A note on the extremal process of the supercritical Gaussian free field. Electron. Commun. Probab. 20 (2015), paper no. 74.CrossRefGoogle Scholar
Davis, R.. Stable limits for partial sums of dependent random variables. Ann. Probab. 11(2) (1983), 262–269.CrossRefGoogle Scholar
Davis, R. and Hsing, T.. Point processes for partial sum convergence for weakly dependent random variables with infinite variance. Ann. Probab. 23(2) (1995), 879–917.CrossRefGoogle Scholar
Doeblin, W.. Remarques sur la théorie métrique des fractions continues. Compos. Math. 7 (1940), 353–371.Google Scholar
Freedman, D.. The Poisson approximation for dependent events. Ann. Probab. 2 (1974), 256–269.CrossRefGoogle Scholar
Galambos, J.. The distribution of the largest coefficient in continued fraction expansions. Quart. J. Math. 23(2) (1972), 147–151.CrossRefGoogle Scholar
Iosifescu, M.. A Poisson law for 𝜓-mixing sequences establishing the truth of a Doeblin’s statement. Rev. Roumaine Math. Pures Appl. 22 (1977), 1441–1447.Google Scholar
Kallenberg, O.. Random Measures, 3rd edn. Akademie-Verlag, Berlin, 1983.Google Scholar
Khintchine, A.. Continued Fractions. University of Chicago Press, Chicago, 1964.Google Scholar
Nakada, H. and Natsui, R.. On the metrical theory of continued fraction mixing fibred systems and its application to Jacobi–Perron algorithm. Monatsh. Math. 138 (2003), 267–288.CrossRefGoogle Scholar
Philipp, W.. A conjecture of Erdös on continued fractions. Acta Arith. 28(4) (1976), 379–386.CrossRefGoogle Scholar
Resnick, S.. Extreme Values, Regular Variation and Point Processes. Springer, New York, 1987.CrossRefGoogle Scholar
Resnick, S.. Heavy-Tail Phenomena. Springer, New York, 2007.Google Scholar
Resnick, S. and de Haan, L.. Second-order regular variation and rates of convergence in extreme-value theory. Ann. Probab. 24(1) (1989), 97–124.Google Scholar
Smith, R. L.. Extreme value theory for dependent sequences via the Stein–Chen method of Poisson approximation. Stochastic Process. Appl. 30(2) (1988), 317–327.CrossRefGoogle Scholar
Tyran-Kamińska, M.. Weak convergence to Lévy stable processes in dynamical systems. Stoch. Dyn. 10(2) (2010), 263–289.CrossRefGoogle Scholar