Article contents
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
Published online by Cambridge University Press: 22 April 2021
Abstract
Let 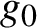 $g_0$ be a smooth pinched negatively curved Riemannian metric on a complete surface N, and let
$g_0$ be a smooth pinched negatively curved Riemannian metric on a complete surface N, and let 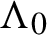 $\Lambda _0$ be a basic hyperbolic set of the geodesic flow of
$\Lambda _0$ be a basic hyperbolic set of the geodesic flow of 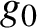 $g_0$ with Hausdorff dimension strictly smaller than two. Given a small smooth perturbation g of
$g_0$ with Hausdorff dimension strictly smaller than two. Given a small smooth perturbation g of 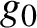 $g_0$ and a smooth real-valued function f on the unit tangent bundle to N with respect to g, let
$g_0$ and a smooth real-valued function f on the unit tangent bundle to N with respect to g, let 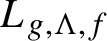 $L_{g,\Lambda ,f}$ (respectively
$L_{g,\Lambda ,f}$ (respectively 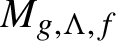 $M_{g,\Lambda ,f}$) be the Lagrange (respectively Markov) spectrum of asymptotic highest (respectively highest) values of f along the geodesics in the hyperbolic continuation
$M_{g,\Lambda ,f}$) be the Lagrange (respectively Markov) spectrum of asymptotic highest (respectively highest) values of f along the geodesics in the hyperbolic continuation 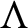 $\Lambda $ of
$\Lambda $ of 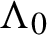 $\Lambda _0$. We prove that for generic choices of g and f, the Hausdorff dimensions of the sets
$\Lambda _0$. We prove that for generic choices of g and f, the Hausdorff dimensions of the sets 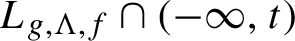 $L_{g,\Lambda , f}\cap (-\infty , t)$ vary continuously with
$L_{g,\Lambda , f}\cap (-\infty , t)$ vary continuously with 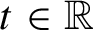 $t\in \mathbb {R}$ and, moreover,
$t\in \mathbb {R}$ and, moreover, 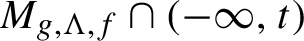 $M_{g,\Lambda , f}\cap (-\infty , t)$ has the same Hausdorff dimension as
$M_{g,\Lambda , f}\cap (-\infty , t)$ has the same Hausdorff dimension as 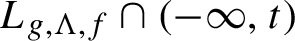 $L_{g,\Lambda , f}\cap (-\infty , t)$ for all
$L_{g,\Lambda , f}\cap (-\infty , t)$ for all 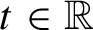 $t\in \mathbb {R}$.
$t\in \mathbb {R}$.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 3
- Cited by


