Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-31T12:04:30.975Z Has data issue: false hasContentIssue false
  • English
  • Français

The Cuntz semigroup and the radius of comparison of the crossed product by a finite group

Part of: $K$-theory and operator algebras Selfadjoint operator algebras

Published online by Cambridge University Press:  10 March 2021

M. ALI ASADI-VASFI ,
NASSER GOLESTANI  and
N. CHRISTOPHER PHILLIPS
M. ALI ASADI-VASFI
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403-1222, USA School of Mathematics, Statistics, and Computer Science, University of Tehran, Tehran, Iran
NASSER GOLESTANI*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran, P. O. Box 14115–134, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P. O. Box 19395–5746, Tehran, Iran
N. CHRISTOPHER PHILLIPS
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403-1222, USA
*
n.golestani@modares.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group, let A be an infinite-dimensional stably finite simple unital C*-algebra, and let 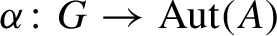$\alpha \colon G \to {\operatorname {Aut}} (A)$ be an action of G on A which has the weak tracial Rokhlin property. Let 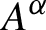$A^{\alpha }$ be the fixed point algebra. Then the radius of comparison satisfies 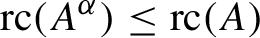${\operatorname {rc}} (A^{\alpha }) \leq {\operatorname {rc}} (A)$ and 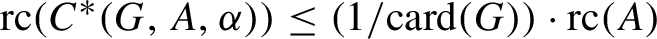${\operatorname {rc}} ( C^* (G, A, \alpha ) ) \leq ({1}/{{{\operatorname{card}}} (G))} \cdot {\operatorname {rc}} (A)$. The inclusion of 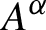$A^{\alpha }$ in A induces an isomorphism from the purely positive part of the Cuntz semigroup 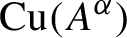${\operatorname {Cu}} (A^{\alpha })$ to the fixed points of the purely positive part of 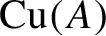${\operatorname {Cu}} (A)$, and the purely positive part of 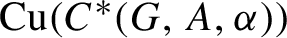${\operatorname {Cu}} ( C^* (G, A, \alpha ) )$ is isomorphic to this semigroup. We construct an example in which 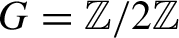$G \,{=}\, {\mathbb {Z}} / 2 {\mathbb {Z}}$, A is a simple unital AH algebra, 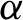$\alpha $ has the Rokhlin property, 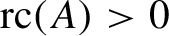${\operatorname {rc}} (A)> 0$, 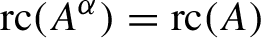${\operatorname {rc}} (A^{\alpha }) = {\operatorname {rc}} (A)$, and 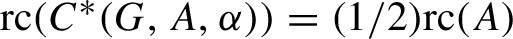${\operatorname {rc}} ({C^* (G, A, \alpha)} ) = ({1}/{2}) {\operatorname {rc}} (A)$.

Keywords

simple C*-algebraradius of comparisoncrossed productweak tracial Rokhlin property

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 19K14: $K_0$ as an ordered group, traces 46L80: $K$-theory and operator algebras (including cyclic theory)

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3541 - 3592
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Akemann, C. A. and Shultz, F.. Perfect C*-algebras. Mem. Amer. Math. Soc. 55(326) (1985).Google Scholar
Amini, M., Golestani, N., Jamali, S. and Phillips, N. C.. Simple tracially $\mathbf{\mathcal{Z}}$ -absorbing C*-algebras, in preparation.Google Scholar
Ara, P., Perera, F. and Toms, A. S.. K-theory for operator algebras. Classification of C*-algebras. Aspects of Operator Algebras and Applications (Contemporary Mathematics, 534). Eds. Ara, P., Lledó, F. and Perera, F.. American Mathematical Society, Providence, RI, 2011, pp. 1–71.CrossRefGoogle Scholar
Archey, D. and Phillips, N. C.. Permanence of stable rank one for centrally large subalgebras and crossed products by minimal homeomorphisms. J. Operator Theory 83 (2020), 353–389.Google Scholar
Asadi, M. B. and Asadi-Vasfi, M. A., The radius of comparison of the tensor product of a C*-algebra with $C(X)$ . J. Operator Theory, to appear. arXiv:2004.03013v1.Google Scholar
Asadi-Vasfi, M. A.. The radius of comparison of the crossed product by a tracially strictly approximately inner action. Preprint, 2020, arXiv:2007.09783v2.Google Scholar
Asadi-Vasfi, M. A.. The Cuntz semigroup of the crossed product of a nonunital C*-algebra by a finite group, in preparation.Google Scholar
Blackadar, B. and Handelman, D.. Dimension functions and traces on C*-algebras. J. Funct. Anal. 45 (1982), 297–340.CrossRefGoogle Scholar
Brown, L. G.. Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. 71 (1977), 335–348.10.2140/pjm.1977.71.335CrossRefGoogle Scholar
Cuntz, J.. Dimension functions on simple C*-algebras. Math. Ann. 233 (1978), 145–153.CrossRefGoogle Scholar
Dǎdǎrlat, M., Nagy, G., Némethi, A. and Pasnicu, C.. Reduction of topological stable rank in inductive limits of C*-algebras. Pacific J. Math. 153 (1992), 267–276.CrossRefGoogle Scholar
Elliott, G. A., Ho, T. M. and Toms, A. S.. A class of simple C*-algebras with stable rank one. J. Funct. Anal. 256 (2009), 307–322.CrossRefGoogle Scholar
Elliott, G. A. and Niu, Z.. On the radius of comparison of a commutative C*-algebra. Canad. Math. Bull. 56 (2013), 737–744.CrossRefGoogle Scholar
Elliott, G. A., Robert, L. and Santiago, L.. The cone of lower semicontinuous traces on a C*-algebra. Amer. J. Math. 133 (2011), 969–1005.CrossRefGoogle Scholar
Fan, Q. and Fang, X.. Stable rank one and real rank zero for crossed products by finite group actions with the tracial Rokhlin property. Chin. Ann. Math. Ser. B 30 (2009), 179–186.CrossRefGoogle Scholar
Forough, M. and Golestani, N.. The weak tracial Rokhlin property for finite group actions on simple C*-algebras. Doc. Math. 25 (2020), 2507–2552.Google Scholar
Gardella, E. and Hirshberg, I.. Strongly outer actions of amenable groups on $\mathbf{\mathcal{Z}}$ -stable C*-algebras. Preprint, 2018, arXiv:1811.00447v2.Google Scholar
Gardella, E., Hirshberg, I. and Santiago, L.. Rokhlin dimension: duality, tracial properties, and crossed products. Ergod. Th. & Dynam. Sys. 41 (2021), 408–460.10.1017/etds.2019.68CrossRefGoogle Scholar
Gardella, E. and Santiago, L.. Equivariant *-homomorphisms, Rokhlin constraints and equivariant UHF-absorption. J. Funct. Anal. 270 (2016), 2543–2590.CrossRefGoogle Scholar
Giordano, T., Kerr, D., Phillips, N. C. and Toms, A.. Crossed Products of C*-Algebras, Topological Dynamics, and Classification (Advanced Courses in Mathematics, CRM Barcelona). Ed. Perera, F.. Birkhäuser/Springer, Cham, 2018.Google Scholar
Golestani, N., in preparation.Google Scholar
Haagerup, U.. Quasitraces on exact C*-algebras are traces. C. R. Math. Acad. Sci. Soc. R. Can. 36 (2014), 67–92.Google Scholar
Hirshberg, I.. Rokhlin dimension, approximate innerness and $\mathbf{\mathcal{Z}}$ -stability. Preprint, 2020, arXiv:2003.09787.Google Scholar
Hirshberg, I. and Orovitz, J.. Tracially $\mathbf{\mathcal{Z}}$ -absorbing C*-algebras. J. Funct. Anal. 265 (2013), 765–785.CrossRefGoogle Scholar
Hirshberg, I. and Phillips, N. C.. Rokhlin dimension: obstructions and permanence properties. Doc. Math. 20 (2015), 199–236.Google Scholar
Hirshberg, I. and Phillips, N. C.. A simple nuclear C*-algebra with an internal asymmetry. Preprint, 2019, arXiv:1909.10728v2.Google Scholar
Husemoller, D.. Fibre Bundles, 3rd edn. Springer, Berlin, 1994.CrossRefGoogle Scholar
Izumi, M.. Finite group actions on C*-algebras with the Rohlin property. II. Adv. Math. 184 (2004), 119–160.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Non-simple purely infinite C*-algebras. Amer. J. Math. 122 (2000), 637–666.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Infinite non-simple C*-algebras: absorbing the Cuntz algebra ${\mathbf{\mathcal{O}}}_{\infty }$ . Adv. Math. 167 (2002), 195–264.10.1006/aima.2001.2041CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Central sequence C*-algebras and tensorial absorption of the Jiang-Su algebra. J. Reine Angew. Math. 695 (2014), 175–214; Erratum. J. Reine Angew. Math. 695 (2014), 215–216.Google Scholar
Lin, H.. An Introduction to the Classification of Amenable C*-Algebras. World Scientific, River Edge, NJ, 2001.Google Scholar
Niu, Z.. Mean dimension and AH-algebras with diagonal maps. J. Funct. Anal. 266 (2014), 4938–4994.CrossRefGoogle Scholar
Orovitz, J., Phillips, N. C. and Wang, Q.. Strict comparison and crossed products, in preparation.Google Scholar
Osaka, H.. Stable rank for crossed products by actions of finite groups on C*-algebras. Preprint, 2017, arXiv:1708.02665v1.Google Scholar
Osaka, H. and Phillips, N. C.. Crossed products by finite group actions with the Rokhlin property. Math. Z. 270 (2012), 19–42.CrossRefGoogle Scholar
Osaka, H. and Teruya, T.. The Jiang-Su absorption for inclusions of unital C*-algebras. Canad. J. Math. 70 (2018), 400–425.CrossRefGoogle Scholar
Osaka, H. and Teruya, T.. Erratum: The Jiang-Su absorption for inclusions of unital C*-algebras. Canad. J. Math. 73(1) (2021) 293–295.CrossRefGoogle Scholar
Perera, F. and Toms, A. S.. Recasting the Elliott conjecture. Math. Ann. 338 (2007), 669–702.10.1007/s00208-007-0093-3CrossRefGoogle Scholar
Phillips, N. C.. Freeness of actions of finite groups on C*-algebras. Operator Structures and Dynamical Systems (Contemporary Mathematics, 503). Eds. de Jeu, M., Silvestrov, S., Skau, C. and Tomiyama, J.. American Mathematical Society, Providence, RI, 2009, pp. 217–257.CrossRefGoogle Scholar
Phillips, N. C.. The tracial Rokhlin property for actions of finite groups on C*-algebras. Amer. J. Math. 133 (2011), 581–636.CrossRefGoogle Scholar
Phillips, N. C.. Large subalgebras. Preprint, 2014, arXiv:1408.5546v2.Google Scholar
Phillips, N. C.. Finite cyclic group actions with the tracial Rokhlin property. Trans. Amer. Math. Soc. 367 (2015), 5271–5300.CrossRefGoogle Scholar
Rieffel, M. A.. Actions of finite groups on C*-algebras. Math. Scand. 47 (1980), 157–176.10.7146/math.scand.a-11882CrossRefGoogle Scholar
Rørdam, M.. On the structure of simple C*-algebras tensored with a UHF-algebra. II. J. Funct. Anal. 107 (1992), 255–269.CrossRefGoogle Scholar
Rørdam, M.. The stable and the real rank of $\mathbf{\mathcal{Z}}$ -absorbing C*-algebras. Internat. J. Math. 15 (2004), 1065–1084.CrossRefGoogle Scholar
Rosenberg, J.. Appendix to O. Bratteli’s paper on “Crossed products of UHF algebras”. Duke Math. J. 46 (1979), 25–26.CrossRefGoogle Scholar
Sato, Y.. Trace spaces of simple nuclear C*-algebras with finite-dimensional extreme boundary. Preprint, 2012, arXiv:1209.3000v1.Google Scholar
Toms, A. S.. Flat dimension growth for C*-algebras. J. Funct. Anal. 238 (2006), 678–708.10.1016/j.jfa.2006.01.010CrossRefGoogle Scholar
Toms, A. S.. Comparison theory and smooth minimal C*-dynamics. Comm. Math. Phys. 289 (2009), 401–433.CrossRefGoogle Scholar
Toms, A. S., White, S. and Winter, W.. $\mathbf{\mathcal{Z}}$ -stability and finite-dimensional tracial boundaries. Int. Math. Res. Not. IMRN 292 (2015), 2707–2727.Google Scholar
Villadsen, J.. On the stable rank of simple C*-algebras. J. Amer. Math. Soc. 12 (1999), 1091–1102.CrossRefGoogle Scholar
Wegge-Olsen, N. E.. K-Theory and C*-Algebras. Oxford University Press, Oxford, 1993.Google Scholar