Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-14T22:47:29.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Decreasing height along continued fractions

Published online by Cambridge University Press:  10 August 2018

GIOVANNI PANTI Open the ORCID record for GIOVANNI PANTI [Opens in a new window]
GIOVANNI PANTI*
Affiliation:
Department of Mathematics, University of Udine, via delle Scienze 206, 33100 Udine, Italy email giovanni.panti@uniud.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The fact that the euclidean algorithm eventually terminates is pervasive in mathematics. In the language of continued fractions, it can be stated by saying that the orbits of rational points under the Gauss map 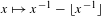$x\mapsto x^{-1}-\lfloor x^{-1}\rfloor$ eventually reach zero. Analogues of this fact for Gauss maps defined over quadratic number fields have relevance in the theory of flows on translation surfaces, and have been established via powerful machinery, ultimately relying on the Veech dichotomy. In this paper, for each commensurability class of non-cocompact triangle groups of quadratic invariant trace field, we construct a Gauss map whose defining matrices generate a group in the class; we then provide a direct and self-contained proof of termination. As a byproduct, we provide a new proof of the fact that non-cocompact triangle groups of quadratic invariant trace field have the projective line over that field as the set of cross-ratios of cusps. Our proof is based on an analysis of the action of non-negative matrices with quadratic integer entries on the Weil height of points. As a consequence of the analysis, we show that long symbolic sequences in the alphabet of our maps can be effectively split into blocks of predetermined shape having the property that the height of points which obey the sequence and belong to the base field decreases strictly at each block end. Since the height cannot decrease infinitely, the termination property follows.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 3 , March 2020 , pp. 763 - 788
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnoux, P. and Hubert, P.. Fractions continues sur les surfaces de Veech. J. Anal. Math. 81 (2000), 35–64.Google Scholar
Arnoux, P. and Schmidt, T. A.. Veech surfaces with nonperiodic directions in the trace field. J. Mod. Dyn. 3(4) (2009), 611–629.Google Scholar
Baladi, V. and Vallée, B.. Euclidean algorithms are Gaussian. J. Number Theory 110(2) (2005), 331–386.Google Scholar
Berg, F.. Dreiecksgruppen mit Spitzen in quadratischen Zahlkörpern. Abh. Math. Sem. Univ. Hamburg 55 (1985), 191–200.Google Scholar
Berthé, V.. Multidimensional Euclidean algorithms, numeration and substitutions. Integers 11B (2011), Paper no. A2, 34pp.Google Scholar
Bombieri, E. and Gubler, W.. Heights in Diophantine Geometry. Cambridge University Press, Cambridge, 2006.Google Scholar
Bouw, I. I. and Möller, M.. Teichmüller curves, triangle groups, and Lyapunov exponents. Ann. of Math. (2) 172(1) (2010), 139–185.Google Scholar
Calta, K. and Schmidt, T. A.. Continued fractions for a class of triangle groups. J. Aust. Math. Soc. 93(1–2) (2012), 21–42.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View towards Number Theory. Springer, Berlin, 2011.Google Scholar
Girondo, E., Torres-Teigell, D. and Wolfart, J.. Shimura curves with many uniform dessins. Math. Z. 271(3–4) (2012), 757–779.Google Scholar
Greenberg, L.. Maximal Fuchsian groups. Bull. Amer. Math. Soc. 69 (1963), 569–573.Google Scholar
Hooper, W. P.. Grid graphs and lattice surfaces. Int. Math. Res. Not. IMRN 2013(12) (2013), 2657–2698.Google Scholar
Katok, S.. Fuchsian Groups. University of Chicago Press, Chicago, 1992.Google Scholar
Lang, S.. Algebra, 3rd edn. Addison-Wesley, Reading, MA, 1993.Google Scholar
Leutbecher, A.. Über die Heckeschen Gruppen G (𝜆). II. Math. Ann. 211 (1974), 63–86.Google Scholar
Maclachlan, C. and Reid, A. W.. The Arithmetic of Hyperbolic 3-Manifolds. Springer, New York, 2003.Google Scholar
Margulis, G. A.. Discrete groups of motions of manifolds of nonpositive curvature. Proc. Int. Congress of Mathematicians (Vancouver, BC, 1974) . Amer. Math. Soc. Transl. Series 2 109 (1977), 33–45.Google Scholar
McMullen, C. T.. Teichmüller geodesics of infinite complexity. Acta Math. 191(2) (2003), 191–223.Google Scholar
Nugent, S. and Voight, J.. On the arithmetic dimension of triangle groups. Math. Comp. 86(306) (2017), 1979–2004.Google Scholar
Panti, G.. A general Lagrange theorem. Amer. Math. Monthly 116(1) (2009), 70–74.Google Scholar
Panti, G.. Slow continued fractions, transducers, and the Serret theorem. J. Number Theory 185 (2018), 121–143.Google Scholar
Schweiger, F.. Multidimensional Continued Fractions. Oxford University Press, Oxford, 2000.Google Scholar
Seibold, F.. Zahlentheoretische Eigenschaften der Heckeschen Gruppen $G(\unicode[STIX]{x1D706})$ und verwandter Transformationsgruppen. Inauguraldissertation, Techn. Univ. München, 1985.Google Scholar
Series, C.. The modular surface and continued fractions. J. Lond. Math. Soc. (2) 31(1) (1985), 69–80.Google Scholar
Singerman, D.. Finitely maximal Fuchsian groups. J. Lond. Math. Soc. (2) 6 (1972), 29–38.Google Scholar
Smillie, J. and Ulcigrai, C.. Geodesic flow on the Teichmüller disk of the regular octagon, cutting sequences and octagon continued fractions maps. Dynamical Numbers—Interplay between Dynamical Systems and Number Theory. American Mathematical Society, Providence, RI, 2010, pp. 29–65.Google Scholar
Smillie, J. and Ulcigrai, C.. Beyond Sturmian sequences: coding linear trajectories in the regular octagon. Proc. Lond. Math. Soc. (3) 102(2) (2011), 291–340.Google Scholar
Takeuchi, K.. Arithmetic triangle groups. J. Math. Soc. Japan 29(1) (1977), 91–106.Google Scholar
Takeuchi, K.. Commensurability classes of arithmetic triangle groups. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24(1) (1977), 201–212.Google Scholar
Veech, W. A.. Teichmüller curves in moduli space, Eisenstein series and an application to triangular billiards. Invent. Math. 97(3) (1989), 553–583.Google Scholar
Ward, C. C.. Calculation of Fuchsian groups associated to billiards in a rational triangle. Ergod. Th. & Dynam. Sys. 18(4) (1998), 1019–1042.Google Scholar