Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T23:45:44.529Z Has data issue: false hasContentIssue false
  • English
  • Français

A dichotomy for bounded displacement equivalence of Delone sets

Part of: Discrete geometry Topological dynamics

Published online by Cambridge University Press:  18 June 2021

YOTAM SMILANSKY  and
YAAR SOLOMON Open the ORCID record for YAAR SOLOMON [Opens in a new window]
YOTAM SMILANSKY
Affiliation:
Department of Mathematics, Rutgers University, New Brunswick, NJ, USA (e-mail: yotam.smilansky@rutgers.edu)
YAAR SOLOMON*
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beersheba, Israel
*
e-mail: yaars@bgu.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that in every compact space of Delone sets in 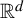${\mathbb {R}}^d$ , which is minimal with respect to the action by translations, either all Delone sets are uniformly spread or continuously many distinct bounded displacement equivalence classes are represented, none of which contains a lattice. The implied limits are taken with respect to the Chabauty–Fell topology, which is the natural topology on the space of closed subsets of 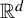${\mathbb {R}}^d$ . This topology coincides with the standard local topology in the finite local complexity setting, and it follows that the dichotomy holds for all minimal spaces of Delone sets associated with well-studied constructions such as cut-and-project sets and substitution tilings, whether or not finite local complexity is assumed.

Keywords

bounded displacement equivalenceDelone setsminimal spacesaperiodic order

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 52C23: Quasicrystals, aperiodic tilings 52C25: Rigidity and flexibility of structures
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 8 , August 2022 , pp. 2693 - 2710
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Aliste-Prieto, J., Coronel, D. and Gambaudo, J. M.. Linearly repetitive Delone sets are rectifiable. Ann. Inst. H. Poincaré Anal. Non Linéaire 30(2) (2013), 275–290.Google Scholar
Adiceam, F., Solomon, Y. and Weiss, B.. Cut-and-project quasicrystals, lattices, and dense forests. J. Lond. Math. Soc., to appear.Google Scholar
Baake, M. and Grimm, U.. Aperiodic Order. Volume 1: A Mathematical Invitation. Cambridge University Press, Cambridge, 2013.CrossRefGoogle Scholar
Burago, D. and Kleiner, B.. Separated nets in Euclidean space and Jacobians of biLipschitz maps. Geom. Funct. Anal. 8(2) (1998), 273–282.CrossRefGoogle Scholar
Burago, D. and Kleiner, B.. Rectifying separated nets. Geom. Funct. Anal. 12 (2002), 80–92.CrossRefGoogle Scholar
Chabauty, C.. Limite d’ensembles et géométrie des nombres. Bull. Soc. Math. France 78 (1950), 143–151.CrossRefGoogle Scholar
Cortez, M. I. and Navas, A.. Some examples of repetitive, non-rectifiable Delone sets. Geom. Topol. 20(4) (2016), 1909–1939.CrossRefGoogle Scholar
de la Harpe, P.. Spaces of closed subgroups of locally compact groups. Preprint, 2008, arXiv:0807.2030.Google Scholar
Dymond, M. and Kaluža, V.. Divergence of separated nets with respect to displacement equivalence. Preprint, 2021, arXiv:2102.13046.Google Scholar
Duneau, M. and Oguey, C.. Displacive transformations and quasicrystalline symmetries. J. Phys. 51(1) (1990), 5–19.CrossRefGoogle Scholar
Duneau, M. and Oguey, C.. Bounded interpolation between lattices. J. Phys. A 24 (1991), 461–475.CrossRefGoogle Scholar
Deuber, W. A., Simonovits, M. and Sós, V. T.. A note on paradoxical metric spaces. Studia Sci. Math. Hungar. 30(1) (1995), 17–24.Google Scholar
Fell, J. M.. A Hausdorff topology for the closed subsets of a locally compact non-Hausdorff space. Proc. Amer. Math. Soc. 13(3) (1962), 472–476.CrossRefGoogle Scholar
Frettlöh, D. and Garber, A.. Pisot substitution sequences, one dimensional cut-and-project sets and bounded diameter sets with fractal boundary. Indag. Math. (N.S.) 29(4) (2018), 1114–1130.CrossRefGoogle Scholar
Frettlöh, D., Garber, A. and Sadun, L.. Number of bounded distance equivalence classes in hulls of repetitive Delone sets. Preprint, 2021, arXiv:2101.02514.CrossRefGoogle Scholar
Frettlöh, D. and Richard, C.. Dynamical properties of almost repetitive Delone sets. Discrete Contin. Dyn. Syst. 34(2) (2014), 531–556.Google Scholar
Frettlöh, D., Smilansky, Y. and Solomon, Y.. Bounded displacement non-equivalence in substitution tilings. J. Combin. Theory Ser. A 177 (2021), 105326.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Haynes, A. and Koivusalo, H.. Constructing bounded remainder sets and cut-and-project sets which are bounded distance to lattice. Israel J. Math. 212 (2016), 189–201.CrossRefGoogle Scholar
Haynes, A., Kelly, M. and Koivusalo, H.. Constructing bounded remainder sets and cut-and-project sets which are bounded distance to lattice, II. Indag. Math. (N.S.) 28(1) (2017), 138–144.CrossRefGoogle Scholar
Haynes, A., Kelly, M. and Weiss, B.. Equivalence relations on separated nets arising from linear toral flows. Proc. Lond. Math. Soc. 109(5) (2014), 1203–1228.CrossRefGoogle Scholar
Kellendonk, J. and Lenz, D.. Equicontinuous Delone dynamical systems. Canad. J. Math. 65(1) (2013), 149–170.CrossRefGoogle Scholar
Kelly, M. and Sadun, L.. Pattern equivariant cohomology and theorems of Kesten and Oren. Bull. Lond. Math. Soc. 47(1) (2015), 13–20.CrossRefGoogle Scholar
Kelly, M. and Sadun, L.. Pattern equivariant mass transport in aperiodic tilings and cohomology. Int. Math. Res. Not. IMRN (2020), rnz310, doi: 10.1093/imrn/rnz310.Google Scholar
Laczkovich, M.. Uniformly spread discrete sets in ${\mathbb{R}}^d$ . J. Lond. Math. Soc. 46(2) (1992), 39–57.CrossRefGoogle Scholar
Lagarias, J. C. and Pleasants, P. A. B.. Repetitive Delone sets and quasicrystals. Ergod. Th. & Dynam. Sys. 23 (2003), 831–867.CrossRefGoogle Scholar
Lee, J. Y. and Solomyak, B.. On substitution tilings and Delone sets without finite local complexity. Discrete Contin. Dyn. Syst. 39(6) (2019), 3149–3177.CrossRefGoogle Scholar
Lenz, D. and Stollmann, P.. Delone dynamical systems and associated random operators. Operator Algebras and Mathematical Physics (Constanta, 2001). Ed. Combes, J. M., Cuntz, J., Elliott, G. A., Nenciu, G., Siedentop, H. and Stratila, S.. Theta, Bucharest, 2003, pp. 267–285.Google Scholar
Magazinov, A. N.. The family of bi-Lipschitz classes of Delone sets in Euclidean space has the cardinality of the continuum. Proc. Steklov Inst. Math. 275 (2011), 87–98.CrossRefGoogle Scholar
McMullen, C. T.. Lipschitz maps and nets in Euclidean space. Geom. Funct. Anal. 8(2) (1998), 304–314.CrossRefGoogle Scholar
Rado, R.. Factorization of even graphs. Q. J. Math. 1 (1949), 95–104.CrossRefGoogle Scholar
Solomon, Y.. Substitution tilings and separated nets with similarities to the integer lattice. Israel J. Math. 181 (2011), 445–460.CrossRefGoogle Scholar
Solomon, Y.. A simple condition for bounded displacement. J. Math. Anal. Appl. 414(1) (2014), 134–148.CrossRefGoogle Scholar
Solomon, Y.. Continuously many bounded displacement non-equivalences in substitution tiling spaces. J. Math. Anal. Appl. 492(1) (2020), 124426.CrossRefGoogle Scholar
Smilansky, Y. and Solomon, Y.. Multiscale substitution tilings. Proc. Lond. Math. Soc. doi: 10.1112/plms.12404. Published online 19 April 2021.Google Scholar