Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-26T09:55:25.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Digit frequencies and self-affine sets with non-empty interior

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Elementary number theory Classical measure theory

Published online by Cambridge University Press:  19 December 2018

SIMON BAKER
SIMON BAKER*
Affiliation:
Mathematics institute, University of Warwick, Coventry, CV4 7AL, UK email simonbaker412@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study digit frequencies in the setting of expansions in non-integer bases, and self-affine sets with non-empty interior. Within expansions in non-integer bases we show that if 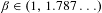$\unicode[STIX]{x1D6FD}\in (1,1.787\ldots )$ then every 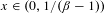$x\in (0,1/(\unicode[STIX]{x1D6FD}-1))$ has a simply normal 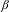$\unicode[STIX]{x1D6FD}$-expansion. We also prove that if 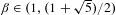$\unicode[STIX]{x1D6FD}\in (1,(1+\sqrt{5})/2)$ then every 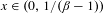$x\in (0,1/(\unicode[STIX]{x1D6FD}-1))$ has a 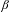$\unicode[STIX]{x1D6FD}$-expansion for which the digit frequency does not exist, and a 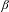$\unicode[STIX]{x1D6FD}$-expansion with limiting frequency of zeros 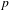$p$, where 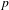$p$ is any real number sufficiently close to 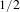$1/2$. For a class of planar self-affine sets we show that if the horizontal contraction lies in a certain parameter space and the vertical contractions are sufficiently close to $1$, then every non-trivial vertical fibre contains an interval. Our approach lends itself to explicit calculation and gives rise to new examples of self-affine sets with non-empty interior. One particular strength of our approach is that it allows for different rates of contraction in the vertical direction.

Keywords

expansions in non-integer basesdigit frequenciesself-affine sets

MSC classification

Primary: 11A63: Radix representation; digital problems
Secondary: 28A80: Fractals 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1755 - 1787
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alcaraz Barrera, R., Baker, S. and Kong, D.. Entropy, topological transitivity, and dimensional properties of unique $q$-expansions. Trans. Amer. Math. Soc., to appear.Google Scholar
Allouche, J,-P., Clarke, M. and Sidorov, N.. Periodic unique beta-expansions: the Sharkovskiǐ ordering. Ergod. Th. & Dynam. Sys. 29 (2009), 1055–1074.Google Scholar
Allouche, J.-P. and Cosnard, M.. The Komornik–Loreti constant is transcendental. Amer. Math. Monthly 107(5) (2000), 448–449.Google Scholar
Allouche, J.-P. and Shallit, J.. The ubiquitous Prouhet–Thue–Morse sequence. Sequences and Their Applications: Proceedings of SETA ’98. Eds. Ding, C., Helleseth, T. and Niederreiter, H.. Springer, London, 1999, pp. 1–16.Google Scholar
Baiocchi, C. and Komornik, V.. Greedy and quasi-greedy expansions in non-integer bases. Preprint, 2007,arXiv:0710.3001 [math.NT].Google Scholar
Baker, S.. Generalised golden ratios over integer alphabets. Integers 14 (2014), Paper No. A15.Google Scholar
Baker, S.. On small bases which admit countably many expansions. J. Number Theory 147 (2015), 515–532.Google Scholar
Baker, S. and Sidorov, N.. Expansions in non-integer bases: lower order revisited. Integers 14 (2014), Paper No. A57.Google Scholar
Borel, E.. Les probabilités dénombrables et leurs applications arithmétiques. Rend. Circ. Mat. Palermo (2) 27 (1909), 247–271.Google Scholar
Dajani, K., Jiang, K. and Kempton, T.. Self-affine sets with positive Lebesgue measure. Indag. Math. (N.S.) 25 (2014), 774–784.Google Scholar
Dajani, K. and Kraaikamp, C.. Random 𝛽-expansions. Ergod. Th. & Dynam. Sys. 23(2) (2003), 461–479.Google Scholar
de Vries, M. and Komornik, V.. Unique expansions of real numbers. Adv. Math. 221(2) (2009), 390–427.Google Scholar
Eggleston, H.. The fractional dimension of a set defined by decimal properties. Q. J. Math. Oxford Ser. 20 (1949), 31–36.Google Scholar
Erdős, P., Horváth, M. and Joó, I.. On the uniqueness of the expansions 1 =∑ i=1∞q -n i. Acta Math. Hungar. 58(3–4) (1991), 333–342.Google Scholar
Erdős, P. and Joó, I.. On the number of expansions 1 =∑ q -n i. Ann. Univ. Sci. Budapest 35 (1992), 129–132.Google Scholar
Erdős, P. and Komornik, V.. Developments in non-integer bases. Acta Math. Hungar. 79(1–2) (1998), 57–83.Google Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications, 3rd edn. John Wiley & Sons, Chichester, 2014.Google Scholar
Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.Google Scholar
Güntürk, C. S.. Simultaneous and hybrid beta-encodings. Information Sciences and Systems, 2008. CISS 2008. 42nd Annual Conference. 2008, pp. 743–748.Google Scholar
Hare, K. and Sidorov, N.. On a family of self-affine sets: Topology, uniqueness, simultaneous expansions. Ergod. Th. & Dynam. Sys. 37 (2017), 193–227.Google Scholar
Hutchinson, J.. Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.Google Scholar
Jordan, T., Shmerkin, P. and Solomyak, B.. Multifractal structure of Bernoulli convolutions. Math. Proc. Cambridge Philos. Soc. 151(3) (2011), 521–539.Google Scholar
Kempton, T.. Private communication, 2016.Google Scholar
Komornik, V., Kong, D. and Li, W.. Hausdorff dimension of univoque sets and Devil’s staircase. Adv. Math. 305 (2017), 165–196.Google Scholar
Komornik, V. and Loreti, P.. Unique developments in non-integer bases. Amer. Math. Monthly 105(7) (1998), 636–639.Google Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Hungar. 11 (1960), 401–416.Google Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Hungar. 8 (1957), 477–493.Google Scholar
Shmerkin, P.. Overlapping self-affine sets. Indiana Univ. Math. J. 55(4) (2006), 1291–1331.Google Scholar
Sidorov, N.. Almost every number has a continuum of beta-expansions. Amer. Math. Monthly 110 (2003), 838–842.Google Scholar
Sidorov, N.. Expansions in non-integer bases: lower, middle and top orders. J. Number Theory 129 (2009), 741–754.Google Scholar