Article contents
Directed harmonic currents near non-hyperbolic linearizable singularities
Published online by Cambridge University Press: 07 July 2022
Abstract
Let 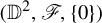 $(\mathbb {D}^2,\mathscr {F},\{0\})$ be a singular holomorphic foliation on the unit bidisc
$(\mathbb {D}^2,\mathscr {F},\{0\})$ be a singular holomorphic foliation on the unit bidisc 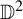 $\mathbb {D}^2$ defined by the linear vector field
$\mathbb {D}^2$ defined by the linear vector field 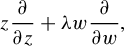 $$ \begin{align*} z \frac{\partial}{\partial z}+ \unicode{x3bb} w \frac{\partial}{\partial w}, \end{align*} $$
$$ \begin{align*} z \frac{\partial}{\partial z}+ \unicode{x3bb} w \frac{\partial}{\partial w}, \end{align*} $$
where 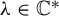 $\unicode{x3bb} \in \mathbb {C}^*$. Such a foliation has a non-degenerate singularity at the origin
$\unicode{x3bb} \in \mathbb {C}^*$. Such a foliation has a non-degenerate singularity at the origin 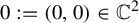 ${0:=(0,0) \in \mathbb {C}^2}$. Let T be a harmonic current directed by
${0:=(0,0) \in \mathbb {C}^2}$. Let T be a harmonic current directed by 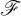 $\mathscr {F}$ which does not give mass to any of the two separatrices
$\mathscr {F}$ which does not give mass to any of the two separatrices 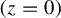 $(z=0)$ and
$(z=0)$ and 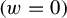 $(w=0)$. Assume
$(w=0)$. Assume 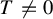 $T\neq 0$. The Lelong number of T at
$T\neq 0$. The Lelong number of T at 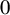 $0$ describes the mass distribution on the foliated space. In 2014 Nguyên (see [16]) proved that when
$0$ describes the mass distribution on the foliated space. In 2014 Nguyên (see [16]) proved that when 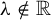 $\unicode{x3bb} \notin \mathbb {R}$, that is, when
$\unicode{x3bb} \notin \mathbb {R}$, that is, when 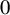 $0$ is a hyperbolic singularity, the Lelong number at
$0$ is a hyperbolic singularity, the Lelong number at 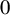 $0$ vanishes. Suppose the trivial extension
$0$ vanishes. Suppose the trivial extension 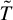 $\tilde {T}$ across
$\tilde {T}$ across 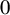 $0$ is
$0$ is 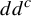 $dd^c$-closed. For the non-hyperbolic case
$dd^c$-closed. For the non-hyperbolic case 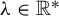 $\unicode{x3bb} \in \mathbb {R}^*$, we prove that the Lelong number at
$\unicode{x3bb} \in \mathbb {R}^*$, we prove that the Lelong number at 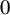 $0$:
$0$:
(1) is strictly positive if
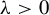 $\unicode{x3bb}>0$;
$\unicode{x3bb}>0$;(2) vanishes if
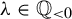 $\unicode{x3bb} \in \mathbb {Q}_{<0}$;
$\unicode{x3bb} \in \mathbb {Q}_{<0}$;(3) vanishes if
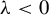 $\unicode{x3bb} <0$ and T is invariant under the action of some cofinite subgroup of the monodromy group.
$\unicode{x3bb} <0$ and T is invariant under the action of some cofinite subgroup of the monodromy group.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 3
- Cited by


