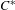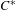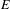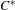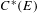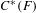Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carlsen, Toke Meier
Eilers, Søren
Ortega, Eduard
and
Restorff, Gunnar
2019.
Flow equivalence and orbit equivalence for shifts of finite type and isomorphism of their groupoids.
Journal of Mathematical Analysis and Applications,
Vol. 469,
Issue. 2,
p.
1088.
Brix, Kevin
and
Carlsen, Toke
2020.
𝐶*-algebras, groupoids and covers of shift spaces.
Transactions of the American Mathematical Society, Series B,
Vol. 7,
Issue. 5,
p.
134.
Matsumoto, Kengo
2020.
A groupoid approach toC*-algebras associated withλ-graph systems and continuous orbit equivalence of subshifts.
Dynamical Systems,
Vol. 35,
Issue. 3,
p.
398.
Carlsen, Toke Meier
Ruiz, Efren
Sims, Aidan
and
Tomforde, Mark
2021.
Reconstruction of groupoids and C⁎-rigidity of dynamical systems.
Advances in Mathematics,
Vol. 390,
Issue. ,
p.
107923.
Matsumoto, Kengo
2025.
Symbolic Dynamical Systems and C*-Algebras.
p.
331.
Matsumoto, Kengo
2025.
Symbolic Dynamical Systems and C*-Algebras.
p.
251.