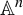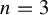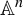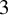Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bisi, Cinzia
Hauenstein, Jonathan D
and
Trung Truong, Tuyen
2024.
Some interesting birational morphisms of smooth affine quadric 3-folds
*
.
Nonlinearity,
Vol. 37,
Issue. 7,
p.
075006.
de Hénon, Julia Xénelkis
2024.
Hénon Maps: A List of Open Problems.
Arnold Mathematical Journal,
Vol. 10,
Issue. 4,
p.
585.