Article contents
Dynamical properties of some adic systems with arbitrary orderings
Published online by Cambridge University Press: 08 March 2016
Abstract
We consider arbitrary orderings of the edges entering each vertex of the (downward directed) Pascal graph. Each ordering determines an adic (Bratteli–Vershik) system, with a transformation that is defined on most of the space of infinite paths that begin at the root. We prove that for every ordering the coding of orbits according to the partition of the path space determined by the first three edges is essentially faithful, meaning that it is one-to-one on a set of paths that has full measure for every fully supported invariant probability measure. We also show that for every 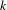 $k$ the subshift that arises from coding orbits according to the first
$k$ the subshift that arises from coding orbits according to the first 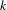 $k$ edges is topologically weakly mixing. We give a necessary and sufficient condition for any adic system to be topologically conjugate to an odometer and use this condition to determine the probability that a random order on a fixed diagram, or a diagram constructed at random in some way, is topologically conjugate to an odometer. We also show that the closure of the union over all orderings of the subshifts arising from codings of the Pascal adic by the first edge has superpolynomial complexity, is not topologically transitive, and has no periodic points besides the two fixed points, while the intersection over all orderings consists of just four orbits.
$k$ edges is topologically weakly mixing. We give a necessary and sufficient condition for any adic system to be topologically conjugate to an odometer and use this condition to determine the probability that a random order on a fixed diagram, or a diagram constructed at random in some way, is topologically conjugate to an odometer. We also show that the closure of the union over all orderings of the subshifts arising from codings of the Pascal adic by the first edge has superpolynomial complexity, is not topologically transitive, and has no periodic points besides the two fixed points, while the intersection over all orderings consists of just four orbits.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 4
- Cited by

