Article contents
Dynamical sets whose union with infinity is connected
Published online by Cambridge University Press: 10 August 2018
Abstract
Suppose that 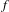 $f$ is a transcendental entire function. In 2011, Rippon and Stallard showed that the union of the escaping set with infinity is always connected. In this paper we consider the related question of whether the union with infinity of the bounded orbit set, or the bungee set, can also be connected. We give sufficient conditions for these sets to be connected and an example of a transcendental entire function for which all three sets are simultaneously connected. This function lies, in fact, in the Speiser class.
$f$ is a transcendental entire function. In 2011, Rippon and Stallard showed that the union of the escaping set with infinity is always connected. In this paper we consider the related question of whether the union with infinity of the bounded orbit set, or the bungee set, can also be connected. We give sufficient conditions for these sets to be connected and an example of a transcendental entire function for which all three sets are simultaneously connected. This function lies, in fact, in the Speiser class.
It is known that for many transcendental entire functions the escaping set has a topological structure known as a spider’s web. We use our results to give a large class of functions in the Eremenko–Lyubich class for which the escaping set is not a spider’s web. Finally, we give a novel topological criterion for certain sets to be a spider’s web.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 4
- Cited by

