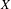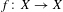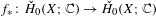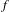Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hernández-Corbato, Luis
Nieves-Rivera, David Jesús
Ruiz del Portal, Francisco R.
and
Sánchez-Gabites, Jaime J.
2023.
On the components of the unstable set of isolated invariant sets.
Topology and its Applications,
Vol. 339,
Issue. ,
p.
108581.
Hernández-Corbato, Luis
Nieves-Rivera, D. J.
Portal, Francisco R. Ruiz del
and
Sánchez-Gabites, J. J.
2025.
A homological bound on entropy in arbitrary compact spaces.
Mathematische Zeitschrift,
Vol. 311,
Issue. 2,