Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T08:12:12.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and topological entropy of 1D Greenberg–Hastings cellular automata

Part of: Waves Topological dynamics

Published online by Cambridge University Press:  09 March 2020

M. KESSEBÖHMER Open the ORCID record for M. KESSEBÖHMER [Opens in a new window] ,
J. D. M. RADEMACHER Open the ORCID record for J. D. M. RADEMACHER [Opens in a new window]  and
D. ULBRICH Open the ORCID record for D. ULBRICH [Opens in a new window]
M. KESSEBÖHMER
Affiliation:
Department 3: Mathematics, University of Bremen, Bibliothekstr. 5, 28359Bremen, Germany email d.ulbrich@uni-bremen.de
J. D. M. RADEMACHER
Affiliation:
Department 3: Mathematics, University of Bremen, Bibliothekstr. 5, 28359Bremen, Germany email d.ulbrich@uni-bremen.de
D. ULBRICH
Affiliation:
Department 3: Mathematics, University of Bremen, Bibliothekstr. 5, 28359Bremen, Germany email d.ulbrich@uni-bremen.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we analyse the non-wandering set of one-dimensional Greenberg–Hastings cellular automaton models for excitable media with $e\geqslant 1$ excited and $r\geqslant 1$ refractory states and determine its (strictly positive) topological entropy. We show that it results from a Devaney chaotic closed invariant subset of the non-wandering set that consists of colliding and annihilating travelling waves, which is conjugate to a skew-product dynamical system of coupled shift dynamics. Moreover, we determine the remaining part of the non-wandering set explicitly as a Markov system with strictly less topological entropy that also scales differently for large 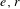$e,r$.

Keywords

cellular automataclassical ergodic theorysymbolic dynamicstopological dynamicslow-dimensional dynamics

MSC classification

Primary: 37B15: Cellular automata 37B20: Notions of recurrence 37B40: Topological entropy
Secondary: 74J35: Solitary waves
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 5 , May 2021 , pp. 1397 - 1430
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author(s) 2020. Published by Cambridge University Press

References

Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114(2) (1965), 309–319.CrossRefGoogle Scholar
Blanchard, F., Kurka, P. and Maass, A.. Topological and measure-theoretic properties of one-dimensional cellular automata. Phys. D 103(1) (1997), 86–99.CrossRefGoogle Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.10.1090/S0002-9947-1971-0274707-XCrossRefGoogle Scholar
Dinaburg, E. I.. A correlation between topological entropy and metric entropy. Dokl. Akad. Nauk SSSR 190 (1970), 19–22.Google Scholar
Durrett, R. and Steif, J. E.. Some rigorous results for the Greenberg–Hastings model. J. Theoret. Probab. 4(4) (1991), 669–690.10.1007/BF01259549CrossRefGoogle Scholar
Greenberg, J. M., Hassard, B. D. and Hastings, S. P.. Pattern formation and periodic structures in systems modeled by reaction–diffusion equations. Bull. Amer. Math. Soc. 84(6) (1978), 1296–1327.10.1090/S0002-9904-1978-14560-1CrossRefGoogle Scholar
Hasselblatt, B., Nitecki, Z. and Propp, J.. Topological entropy for non-uniformly continuous maps. Discrete Contin. Dyn. Syst. A 22(1&2) (2008), 201–213.Google Scholar
Hurd, L. P., Kari, J. and Culik, K.. The topological entropy of cellular automata is uncomputable. Ergod. Th. & Dynam. Sys. 12(2) (1992), 255–265.10.1017/S0143385700006738CrossRefGoogle Scholar
Izhikevich, E. M.. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. MIT Press, Cambridge, MA, 2010.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications) . Cambridge University Press, Cambridge, 1997.Google Scholar
Krinsky, V. and Swinney, H.. Wave and Patterns in Biological and Chemical Excitable Media. North-Holland, Amsterdam, 1991.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511626302CrossRefGoogle Scholar
Manz, N. and Steinbock, O.. Propagation failures, breathing pulses, and backfiring in an excitable reaction–diffusion system. Chaos 16(3) (2006).10.1063/1.2266993CrossRefGoogle Scholar
Meyerovitch, T.. Finite entropy for multidimensional cellular automata. Ergod. Th. & Dynam. Sys. 28(4) (2008), 1243–1260.CrossRefGoogle Scholar
Pearson, J. E.. Complex patterns in a simple system. Science 261(5118) (1993), 189–192.10.1126/science.261.5118.189CrossRefGoogle Scholar
Perraud, J.-J., De Wit, A., Dulos, E., De Kepper, P., Dewel, G. and Borckmans, P.. One-dimensional ‘spirals’: Novel asynchronous chemical wave sources. Phys. Rev. Lett. 71 (1993), 1272–1275.CrossRefGoogle ScholarPubMed
Petrov, V., Scott, S. K. and Showalter, K.. Excitability, wave reflection, and wave splitting in a cubic autocatalysis reaction–diffusion system. Philos. Trans. Roy. Soc. Lond. A 347 (1994), 631–642.Google Scholar
Reynolds, W. N., Pearson, J. E. and Ponce-Dawson, S.. Dynamics of self-replicating patterns in reaction diffusion systems. Phys. Rev. Lett. 72(17) (1994), 2797.CrossRefGoogle ScholarPubMed
Ulbrich, D.. Dynamics of the 1D Greenberg–Hastings cellular automaton. Master’s thesis, Universität Bremen, 2016, supervised by J. D. M. Rademacher and T. Samuel.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 2000.Google Scholar
Yangeng, W., Wei, G. and Campbell, W. H.. Sensitive dependence on initial conditions between dynamical systems and their induced hyperspace dynamical systems. Topol. Appl. 156(4) (2009), 803–811.Google Scholar