Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Depauw, Jérôme
1997.
Théorème ergodique ponctuel pour cocycle de degré deux.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 325,
Issue. 1,
p.
87.
Depauw, Jérôme
2007.
Degree two ergodic theorem for divergence-free stationary random fields.
Israel Journal of Mathematics,
Vol. 157,
Issue. 1,
p.
283.
Boivin, Daniel
2009.
Tail estimates for homogenization theorems in random media.
ESAIM: Probability and Statistics,
Vol. 13,
Issue. ,
p.
51.
Björklund, Michael
2010.
The asymptotic shape theorem for generalized first passage percolation.
The Annals of Probability,
Vol. 38,
Issue. 2,
Barlow, M. T.
and
Deuschel, J.-D.
2010.
Invariance principle for the random conductance model with unbounded conductances.
The Annals of Probability,
Vol. 38,
Issue. 1,
Cotar, Codina
and
Deuschel, Jean-Dominique
2012.
Decay of covariances, uniqueness of ergodic component and scaling limit for a class of $\nabla\phi$ systems with non-convex potential.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 48,
Issue. 3,
Cotar, Codina
and
Külske, Christof
2015.
Uniqueness of gradient Gibbs measures with disorder.
Probability Theory and Related Fields,
Vol. 162,
Issue. 3-4,
p.
587.
Andres, Sebastian
Deuschel, Jean-Dominique
and
Slowik, Martin
2015.
Invariance principle for the random conductance model in a degenerate ergodic environment.
The Annals of Probability,
Vol. 43,
Issue. 4,
Boivin, Daniel
and
Lê, Thi Thu Hien
2020.
Large deviations for Brownian motion in a random potential.
ESAIM: Probability and Statistics,
Vol. 24,
Issue. ,
p.
374.
Cornulier, Yves
and
Tessera, Romain
2021.
On the vanishing of reduced 1-cohomology for Banach representations.
Annales de l'Institut Fourier,
Vol. 70,
Issue. 5,
p.
1951.
Christensen, Johannes
and
Vaes, Stefaan
2022.
KMS Spectra for Group Actions on Compact Spaces.
Communications in Mathematical Physics,
Vol. 390,
Issue. 3,
p.
1341.
Brown, Aaron
Hertz, Federico Rodriguez
and
Wang, Zhiren
2023.
Smooth ergodic theory of $ \mathbb {Z}^d $-actions.
Journal of Modern Dynamics,
Vol. 19,
Issue. 0,
p.
455.

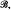 , μ,
, μ,