Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T06:00:32.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Escape of mass and entropy for geodesic flows

Published online by Cambridge University Press:  28 June 2017

FELIPE RIQUELME  and
ANIBAL VELOZO
FELIPE RIQUELME
Affiliation:
IMA, Pontificia Universidad Católica de Valparaíso, Blanco Viel 596, Cerro Barón, Valparaíso, Chile email friquelme.math@gmail.com
ANIBAL VELOZO
Affiliation:
Princeton University, Princeton, NJ 08544-1000, USA email avelozo@math.princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the ergodic theory of the geodesic flow on negatively curved geometrically finite manifolds. We prove that the measure-theoretical entropy is upper semicontinuous when there is no loss of mass. In the case where mass is lost, the critical exponents of parabolic subgroups of the fundamental group have a significant meaning. More precisely, the failure of upper-semicontinuity of the entropy is determined by the maximal parabolic critical exponent. We also study the pressure of positive Hölder-continuous potentials going to zero through the cusps. We prove that the pressure map 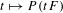$t\mapsto P(tF)$ is differentiable until it undergoes a phase transition, after which it becomes constant. This description allows us, in particular, to compute the entropy of the geodesic flow at infinity.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 2 , February 2019 , pp. 446 - 473
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L.. Thermodycamic Formalism and Applications to Dimension Theory (Progress in Mathematics, 294) . Birkhäuser, Basel, 2011.Google Scholar
Bowditch, B. H.. Geometrical finiteness with variable negative curvature. Duke Math. J. 77(1) (1995), 229–274.Google Scholar
Coudene, Y.. Gibbs measures on negatively curved manifolds. J. Dyn. Control Syst. 9(1) (2003), 89–101.Google Scholar
Dal’bo, F., Otal, J.-P. and Peigné, M.. Séries de Poincaré des groupes géométriquement finis. Israel J. Math. 118 (2000), 109–124.Google Scholar
Dinaburg, E. I.. The relation between topological entropy and metric entropy. Dokl. Akad. Nauk SSSR 190 (1970), 19–22.Google Scholar
Einsiedler, M., Kadyrov, S. and Pohl, A.. Escape of mass and entropy for diagonal flows in real rank one situations. Israel J. Math. 210(1) (2015), 245–295.Google Scholar
Handel, M. and Kitchens, B.. Metrics and entropy for non-compact spaces. Israel J. Math. 91(1–3) (1995), 253–271; With an appendix by Daniel J. Rudolph.Google Scholar
Iommi, G., Riquelme, F. and Velozo, A.. Entropy in the cusp and phase transitions for geodesic flows. Israel J. Math. to appear.Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.Google Scholar
Keller, G.. Equilibrium States in Ergodic Theory (London Mathematical Society, 42) . Cambridge University Press, Cambridge, 1998.Google Scholar
Manning, A.. Topological entropy for geodesic flows. Ann. of Math. (2) 110(3) (1979), 567–573.Google Scholar
Newhouse, S.. Continuity properties of entropy. Ann. of Math. (2) 129(2) (1989), 215–235.Google Scholar
Otal, J.-P. and Peigné, M.. Principe variationnel et groupes kleiniens. Duke Math. J. 125(1) (2004), 15–44.Google Scholar
Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136(3–4) (1976), 241–273.Google Scholar
Paulin, F., Pollicott, M. and Barbara, S.. Equilibrium states in negative curvature. Astérisque 373 (2015), viii+281.Google Scholar
Rees, M.. Checking ergodicity of some geodesic flows with infinite gibbs measure. Ergod. Th. & Dynam. Sys. 1(1) (1981), 107–133.Google Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153(3–4) (1984), 259–277.Google Scholar
Velozo, A.. Phase transitions for geodesic flows and the geometric potential. Preprint, arXiv:1704.02562.Google Scholar
Yomdin, Y.. Volume growth and entropy. Israel J. Math. 57(3) (1987), 285–300.Google Scholar
Yue, C.. The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Trans. Amer. Math. Soc. 348(12) (1996), 4965–5005.Google Scholar