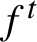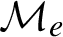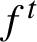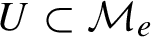Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burago, Dmitri
Chen, Dong
and
Ivanov, Sergei
2023.
Flexibility of sections of nearly integrable Hamiltonian systems.
Communications in Contemporary Mathematics,
Vol. 25,
Issue. 04,